Cours de mathématiques de 3eFonctions linéaires et affines |
|
|
|
|
Video |
|
Texte
On appelle fonction linéaire de R → R une fonction qui à tout x associe ax où "a" est un nombre réel appelé un coefficient. On note
f : x → f(x) = ax
Cette suite de signes se lit : "f est la fonction qui à tout x associe f de x égal ax"
On appelle fonction affine de R → R une fonction qui à tout x associe ax + b où "a" et "b" sont des nombres réels appelés coefficients. On note
f : x → f(x) = ax + b
Cette suite de signes se lit : "f est la fonction qui à tout x associe f de x égal ax plus b".
Quand on a une fonction de R vers R, une des premières questions qui se pose est "quel est son graphe ?", c'est-à-dire quel est le dessin, dans un plan avec un repère, formé par l'ensemble des points de coordonnées [ x ; f(x) ] ?
Parfois on note y pour f(x), et on veut dessiner tous les points [ x ; y ] tels que y = ax + b.
Les graphes des fonctions linéaires et affines sont particulièrement simples : ce sont des lignes droites. Cela résulte du théorème de Thalès;
Exemple 1 : graphe de f(x) = 2x
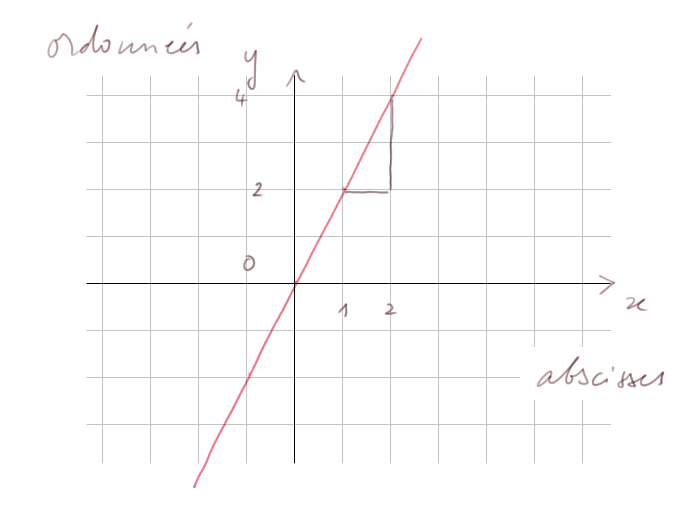
La droite passe par le point [ 0 ; 0 ], par le point [ 1 ; 2 ], par le point [ 2 ; 4 ], etc. Chaque fois que, tout en restant sur la droite, on se déplace d'une distance Δx sur l'axe des x, on se déplace d'une distance Δy = 2 fois Δx sur l'axe des ordonnées.
Exemple 2 : graphe de f(x) = x/3
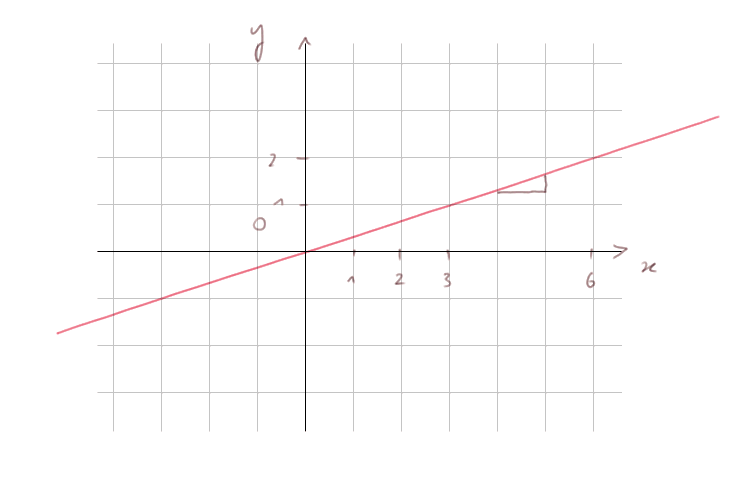
La droite passe toujours par [ 0 ; 0 ]. Elle passe aussi par [ 1 ; 1/3 ], [ 2 ; 2/3], [ 3 ; 1 ], etc. Chaque fois que, tout en restant sur la droite, on se déplace d'une distance Δx sur l'axe des abscisses, on se déplace d'une distance Δy = Δx divisé par trois sur l'axe des y.
Le graphe d'une fonction affine n'est pas plus compliqué.
Exemple 3 : graphe de y = x/3 + 1
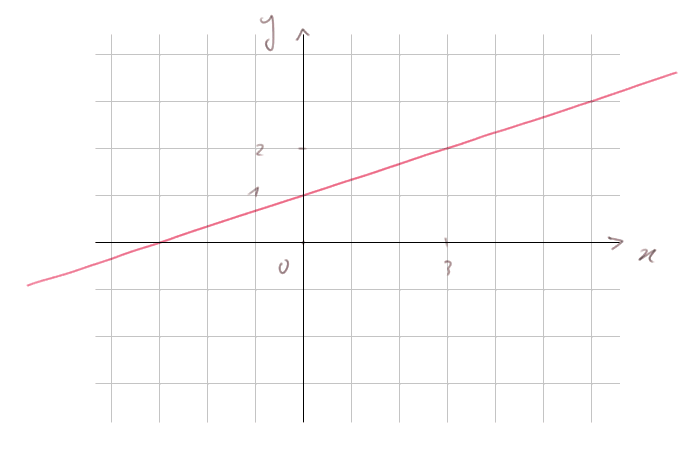
Quand x = 0, y = 1. Quand x = 1, y = 1,33333... etc.
Dans une fonction de la forme y = ax + b,
- "a" s'appelle "le coefficient directeur", ou aussi "la pente de la droite"
- "b" s'appelle "l'ordonnée à l'origine"
"a" et "b" ont des interprétations géométriques très simples. Voyons de nouveau y = x/3 + 1
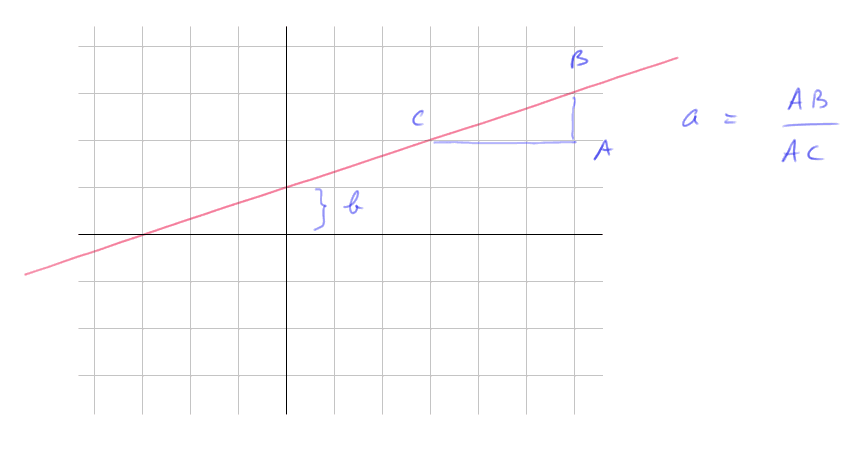
On voit que si x = 0, y = b. C'est pour ça que b s'appelle l'ordonnée à l'origine. Et pour tout triangle rectangle ABC construit avec BC pour hypoténuse, sur la droite, et AB vertical, et AC horizontal, a est égal au ratio AB/AC. C'est pour ça que a s'appelle la pente de la droite.
Exercices :
- Tracer les graphes y = x + 2 et y = -2x + 5
- Où les deux droites se rencontrent-elles ?