Cours de mathématiques de 3eInéquations et inégalités |
|
|
|
|
Video |
|
Texte
Les inéquations et les inégalités sont comparables aux équations et aux identités, mais où le signe = est remplacé par < ou ≤ ou ≥ ou >.
Rappel : une équation est une ou deux expressions littérales/numériques faisant intervenir un nombre inconnu x, et exprimant une contrainte sur x avec le signe égal. Il faut trouver le nombre x, soit avec de l'algèbre, soit en traçant une courbe.
Exemple 1 : trouver x tel que 4(x + 3) = x + 63. Faisons de l'algèbre :
→ 4x + 12 = x + 63
→ 3x + 12 = 63
→ 3x = 51
→ x = 17
Exemple 2 : trouver x tel que x(x + 1)(x + 2) = 10. Ici l'algèbre est un peu compliquée. On va plutôt tracer une courbe.
Dans le plan, muni d'un repère, on trace tous les points avec pour coordonnées [ x et x(x + 1)(x + 2) - 10 ] pour x entre -6 et +5. On voit pour quel x l'expression x(x + 1)(x + 2) - 10 est égale à 0. C'est pour x ≈ 1,3.
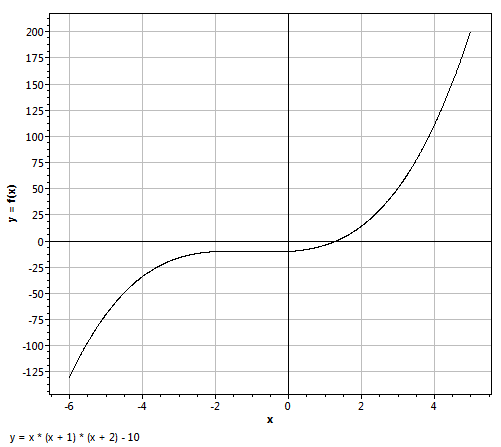
En travaillant au tableur, on peut trouver que la solution est plus précisément ≈ 1,31.
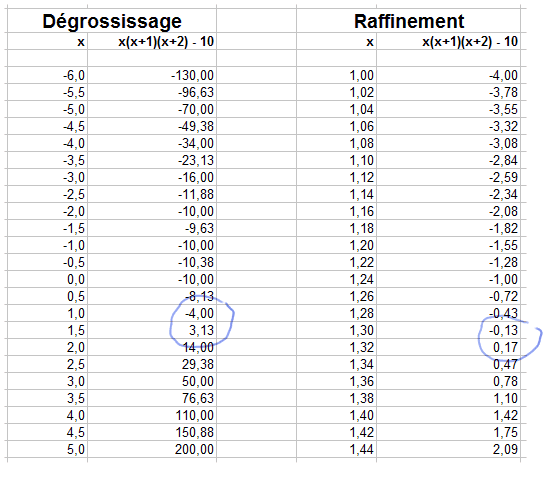
Rappel 2 : une identité est une égalité entre 2 expressions littérales qui est toujours vraie. Exemple : (a + b)2 = a2 + 2ab + b2.
Inéquations
Exemple 1 : trouver tous les x tels que (4x + 2)/3x > 1.
On va faire de l'algèbre exactement comme avec les équations. On peut ajouter et soustraire de chaque côté, multiplier et diviser de chaque côté. Mais si on multiplie ou divise par un nombre négatif, il faut changer le signe > en <.
- Pour tous les x positifs, la contrainte devient 4x + 2 > 3x , d'où x > -2 et x > 0. Donc x > 0
- Et pour tous les x négatifs, la contrainte devient 4x + 2 < 3x, d'où x < -2 et x < 0. Donc x < -2.
La solution complète est donc : x doit être inférieur à -2 ou supérieur à 0.
Le mieux quand on a une expression algébrique au comportement un peu complexe est de la dessiner, c'est-à-dire, ici, de représenter la courbe de tous les points de coordonnées [ x ; (4x + 2) / 3x ]. On verra plus facilement tous les x pour lesquels (4x + 2)/3x est supérieur à 1.
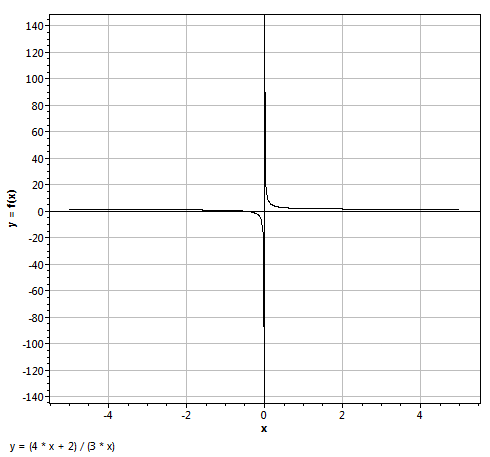
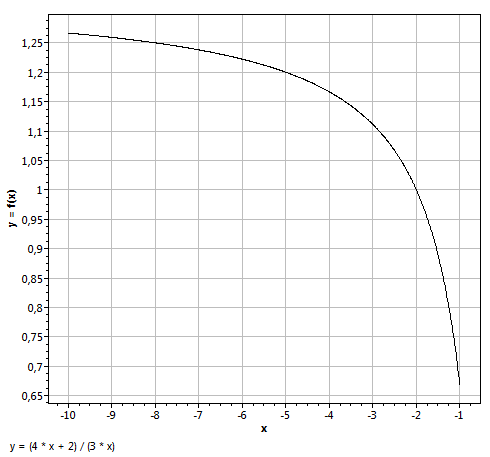
Regardons cette courbe, qui s'appelle une "hyperbole", à une échelle plus grande, entre -10 et -1, et entre 1 et 10 :
| Comportement quand x est négatif | Comportement quand x est positif |
 |
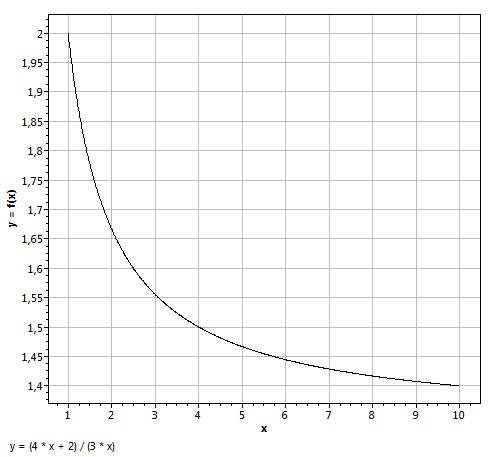 |
Maintenant on voit bien que pour x inférieur à -2 la courbe est supérieure à 1. Pour x entre -2 et 0 la courbe plonge sous +1 vers moins l'infini. Et pour x positif la courbe est toujours au dessus de 1.
Exemple 2 :
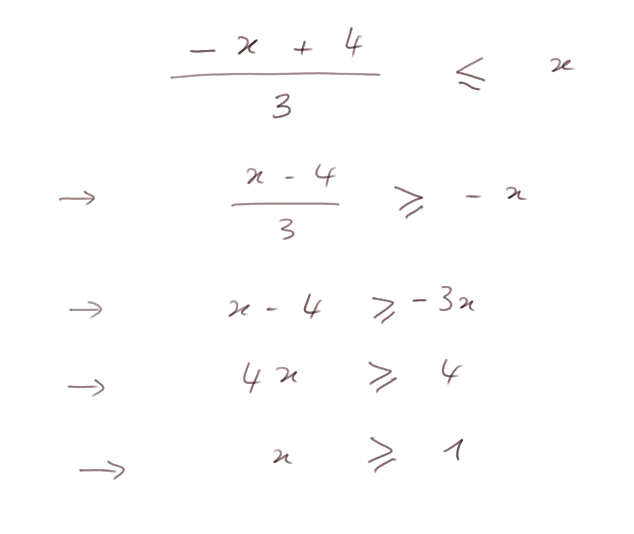
Inégalités
Une inégalité, c'est la formulation d'une comparaison entre deux expressions littérales qui est toujours vraie. Exemple : ∀ a et b (le signe ∀ se lit "quels que soient"), des nombres quelconques (entiers, relatifs, rationnels ou irrationnels), on a

Démonstration : on va transformer cette inégalité en quelques inégalités équivalentes, jusqu'à ce qu'on arrive à quelque chose de clairement vrai.
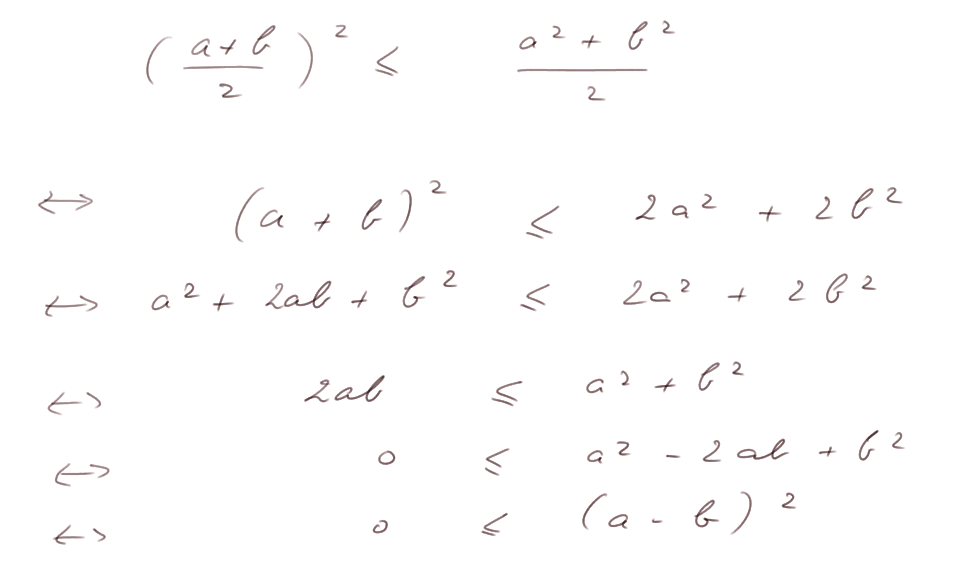
Cette inégalité a une interprétation géométrique : on considère la courbe formée de tous les points de coordonnées [ x, x2 ]
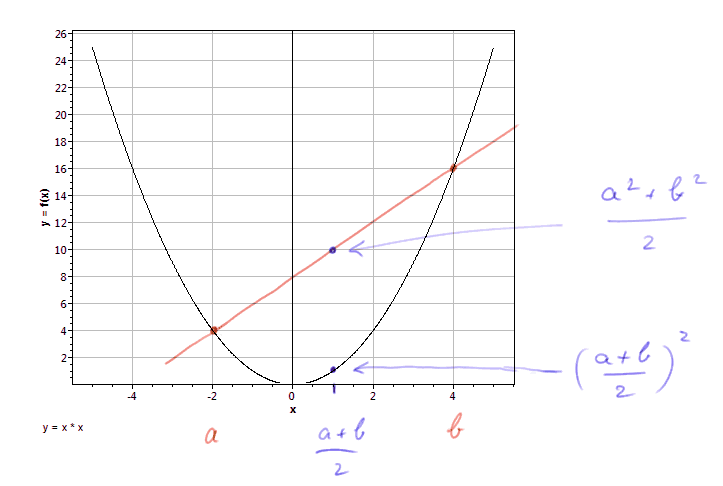
Le nombre (a + b)/2 sur l'axe des x donne le point [ (a + b)/2, (a + b)2/4 ]. Par ailleurs le point au milieu des points [ a, a2 ] et [ b, b2 ] a pour coordonnées [ (a + b)/2, a2 + b2/2 ]. Ce sont les moyennes des abscisses et des ordonnées de [ a, a2 ] et [ b, b2 ].
Comme la courbe, qui est une parabole, est convexe, le point [ (a + b)/2, a2 + b2/2 ] est au dessus du point [ (a + b)/2, (a + b)2/4 ].
Pour des raisons comparables, soit n nombres a1, a2, ... an et n coefficients c1, c2, ... c n tels que c1 + c2 + ... + c n = 1 et tous les c i sont positifs, alors
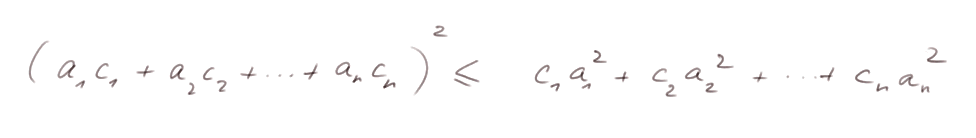
Exemple : soit a1 = 2, a2 = 3 et a3 = 5. Et c1 = 60%, c2 = 25% et c3 = 15%.
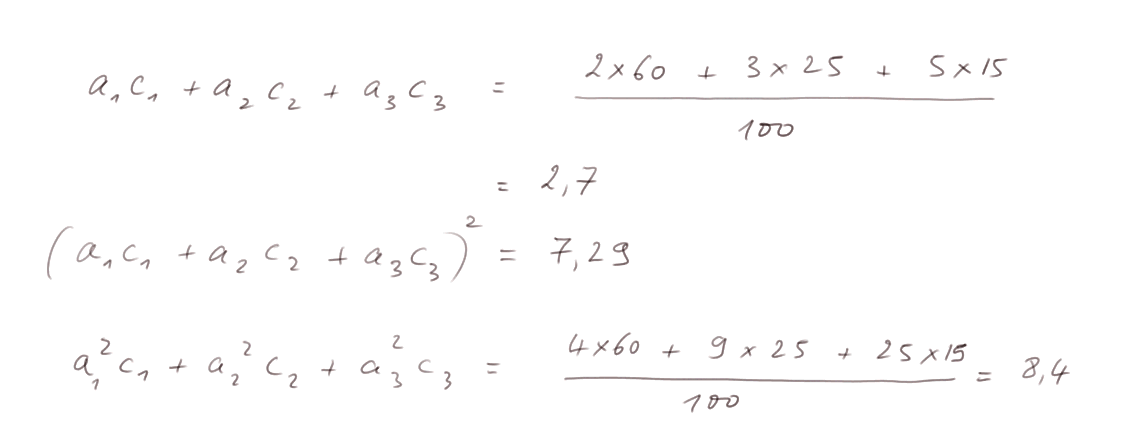
Exercices :
- Vérifier la dernière inégalité avec a1 = 10, a2 = -3 et a3 = 2. Et c1 = 25%, c2 = 40% et c3 = 35%.