Cours de mathématiques de 4eNombres entiers négatifs |
|
Video |
Texte
On a rencontré le besoin de créer des nouveaux nombres quand on a regardé des opérations comme 2 - 7 = ?
Les nombres entiers négatifs sont des nouveaux nombres qui donnent un sens à cette opération.
La création de nouveaux nombres pour donner un sens au résultat d'une opération est quelque chose que nous avons déjà rencontré. C'est ce que nous avons fait en créant les fractions pour que l'opération 2 divisé par 3 ait un résultat. Pour noter ce nouveau nombre, on ne s'est pas compliqué la vie : on l'a noté 2/3.
Les fractions avaient une représentation naturelle, y compris leur addition, soustraction, et multiplication et division.

Les nombres négatifs vont être des marques à gauche de l'origine sur la droite habituelle servant à représenter les nombres.
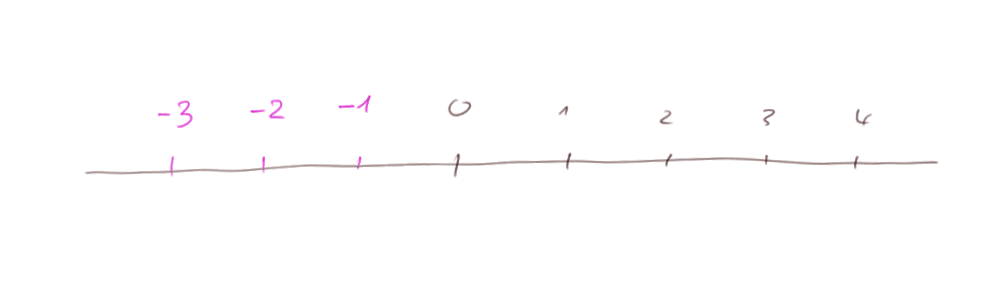
L'addition d'un entier habituel correspondait à un déplacement vers la droite. Et la soustraction correspondait à un déplacement vers la gauche (quand on soustrayait un entier habituel, qu'on appelera maintenant un "entier positif").
1 + 3 = 4
Additionner -1 consistera à se déplacer d'un cran vers la gauche.
3 + (-1) = 2, et c'est donc pareil que 3 -1
Multiplier un nombre négatif par un nombre positif (exemple 3 fois "-5") ne pose pas de problèmes : c'est l'addition de -5 trois fois.
3 fois (-5) = (-5) + (-5) + (-5) = -15.
Le problème va être de donner un sens à la multiplication par -1. Car la multiplication par un nombre négatif ne correspond plus à la notion naturelle de série d'additions.
Comme l'on veut que la distributivité de la multiplication reste vraie, on a forcément 0 = [ 1 + (-1)] x 3 = 1 x 3 + (-1) x 3. Donc (-1) x 3 = - (1 x 3) = -3.
La multiplication d'un nombre par (-1) consiste à faire une rotation de 180° autour de zéro à partir de ce nombre.
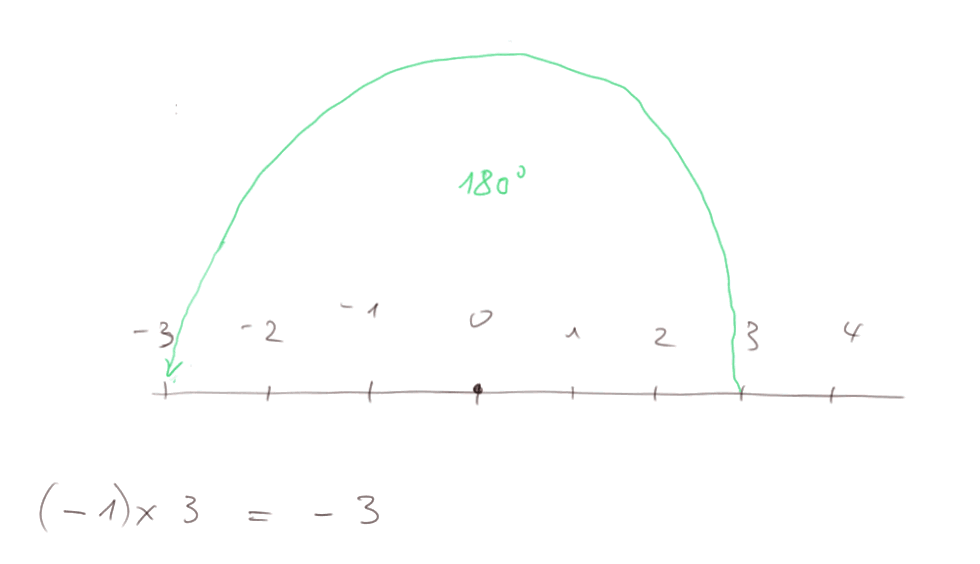
Multiplier par un nombre négatif quelconque (par exemple -7) sera toujours équivalent à multiplier d'abord pas le nombre positif correspondant (ici +7), puis multiplier par (-1).
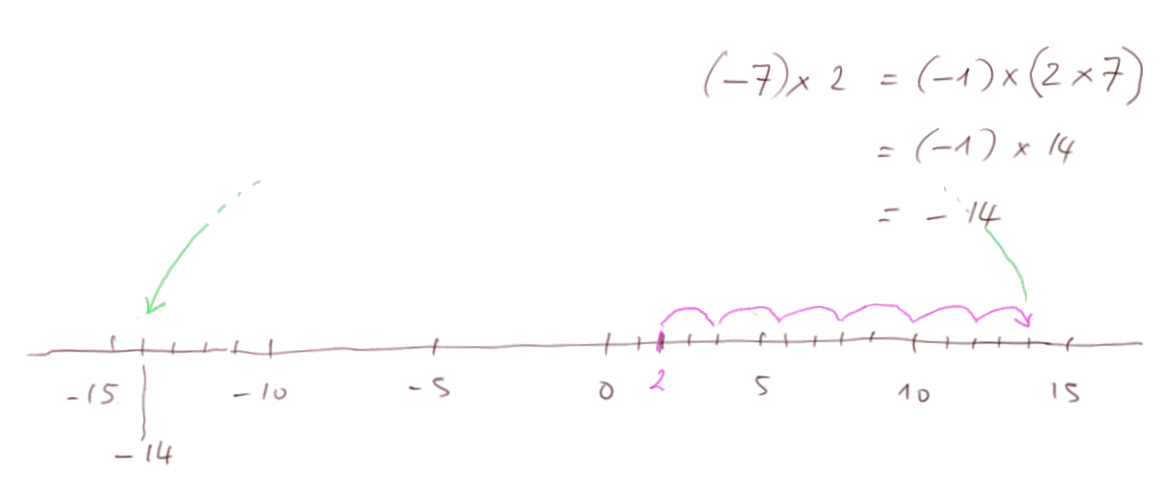
Avec cette règle, la multiplication reste commutative : (-7) x 2 = -14 = (-7) + (-7) = 2 x (-7). Et elle reste distributive par rapport à l'addition, c'est-à-dire que a x (b + c) = ab + ac.
Question : quel est le résultat de (-1) x (-1) ? Eh bien avec la règle de la rotation de 180° c'est simple. On part de (-1) et on fait une rotation de 180°. On tombe sur 1.
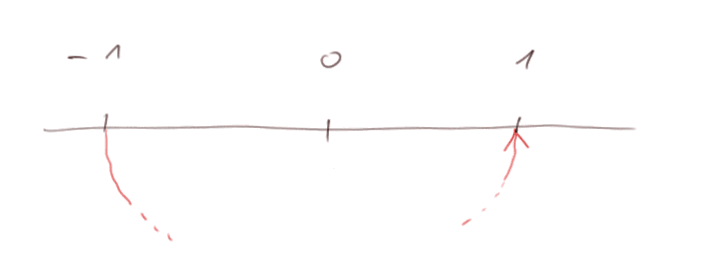
Donc (-1) x (-1) = 1.
De même (-7) x (-5) = (-1) x (7 x (-5)) = (-1) x (-35) = 35. On le note parfois +35.
Les nombres négatifs servent à beaucoup de choses dans la vie courante :
- Noter des positions par rapport à une "position zéro" sur une ligne.
- Compter les années avant J.-C.
- Donner une profondeur sous le niveau de la mer.
- Mesurer notre "position financière" quand on doit de l'argent à quelqu'un (c'est-à-dire qu'il est notre créancier, ou créditeur).
- etc.
Ce qu'il faut retenir c'est que les nombres négatifs ont été créés pour que l'opération "n - m" ait toujours un sens, quels que soient les entiers n et m.
Retenir que (-1) x 15 = -15 (c'est la règle de la rotation pour définir la multiplication par -1).
Au lycée nous introduirons encore d'autres nombres, appelés "complexes", en particulier un nombre noté "i", tel que i x i = -1. Rappelons-nous qu'on a introduit chaque fois nos nouveaux nombres pour donner des solutions à des "équations impossibles", par exemple n + 5 = 2, ou bien n x 3 = 7. Eh bien on introduira donc aussi des nombres tels que c x c = -3 ait une solution (il y en aura même deux).
La multiplication par le nombre "i", correspondra à une rotation autour du point 0 de 90° dans le sens contraire des aiguilles d'une montre, et donc enverra un point de la droite horizontale habituelle vers un point du plan en dehors de la droite. Ces nombres complexes et leur interprétation à l'aide de la géométrie des rotations ont des quantités de propriétés merveilleuses, et servent dans tous les domaines des mathématiques et de la physique.
Ils ont été appelés "complexes" ou même "imaginaires" car, comme pour les nombres irrationnels ou négatifs, ils ont d'abord beaucoup intrigué et troublé les mathématiciens. En fait nous découvrirons qu'ils rendent l'étude des fonctions et de la géométrie beaucoup plus simple qu'avec les seuls nombres réels.
Un dernier commentaire sur les nombres négatifs: c'est un premier exemple de la grande liberté qu'on a en mathématiques de créer des nouvelles "choses". Le nombre négatif "moins trois" est la "chose" qui résout l'équation 5 + x = 2.
Evidemment, quand on crée des "nouvelles choses", on ne le fait pas de manière totalement arbitraire. En fait on crée des nouveaux objets, obéissant à des règles, et ayant donc une structure, dans un but donné: en général étendre le domaine dans lequel un problème a un sens. Plus généralement, on crée une "structure" qui modélise bien des phénomènes physiques, comme par exemple un ascenseur qui permet de descendre dans une cave au troisième sous-sol, ou une dette envers quelqu'un.
Dans d'autres circonstances, on crée des structures de manière encore plus arbitraires, par exemple au jeu d'échec quand on crée le cavalier et décide de la façon dont il se déplace. On crée aussi d'autres règles de manière arbitraire, par exemple "la prise en passant".
En mathématiques, les structures et les règles qu'on crée sont moins arbitraires que dans la conception d'un nouveau jeu. Elles ont toujours pour but de modéliser des phénomènes -- lesquels peuvent être eux-mêmes plus ou moins physiques, ou au contraire plus ou moins abstraits. Mais on veut toujours "représenter quelque chose".
Dans la leçon suivante nous étudierons les fractions négatives.
Exercices
- Quel est le résultat de (-2) x 5 ?
- Quel est le résultat de (-2) x (-2) ?
- Quel est le résultat de (5 - 7) x 3 ?
Plan général du cours
Contacter le professeur
Réponses
- Quel est le résultat de (-2) x 5 ? Rép : -10
- Quel est le résultat de (-2) x (-2) ? Rép : 4
- Quel est le résultat de (5 - 7) x 3 ? Rép : -6