Cours de mathématiques de 5e Cercles et cylindres
Video

Texte

De même que du polygone dans le plan on est passé au prisme dans l'espace, on passe du cercle dans le plan au cylindre dans l'espace.

Comme un prisme, un cylindre peut être droit ou oblique.

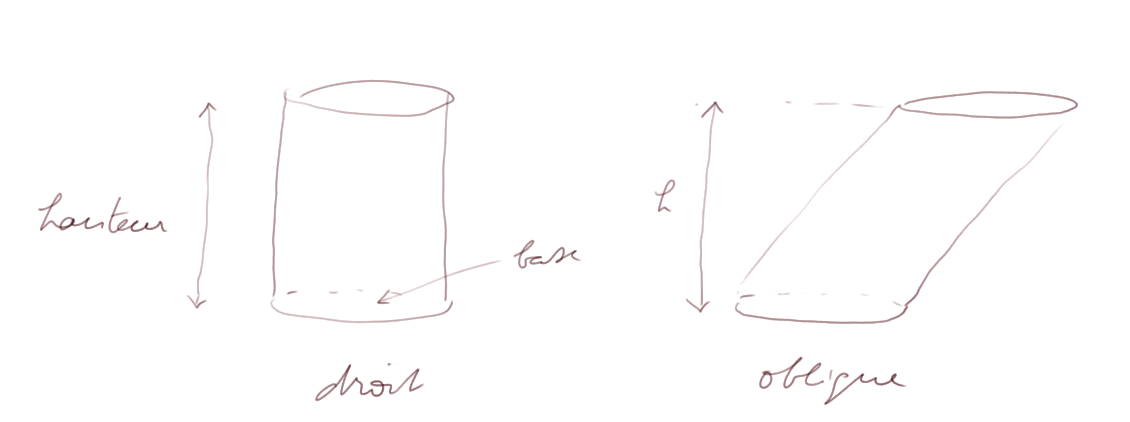
Intersections des cylindres et des plans : un cylindre (droit ou oblique) coupé par un plan parallèle à sa base découpe dans le plan d'intersection un cercle. Pour les autres plans (inclinés par rapport à la génératrice du cylindre) on obtient des ellipses.

 

 

Propriétés des cylindres droits : un cylindre droit a un axe de symétrie verticale. La surface de la paroi verticale est égale à 2 π R x h. Un cylindre est la figure limite d'un prisme dont le polygone de base se rapproche d'un cercle.

Volume d'un cylindre droit : de même que pour un prisme droit, le volume est V = S x h (où S est la surface de la base, et h la hauteur), pour un cylindre droit V = S x h.

La formule reste vraie pour un cylindre oblique. Pensez à une pile de pièces de monnaie d'abord empilées en cylindre droit, puis toutes un peu déplacées pour faire un cylindre oblique : on ne change pas la base, ni la hauteur, ni le volume. Donc

V = S x h

pour tous les cylindres.

La surface de la paroi d'un cylindre oblique est plus grande que celle du cylindre droit correspondant (i.e. de même base et même hauteur).

Exercice : On a une boîte de conserve cylindrique (droite) dont la base a un rayon de 5 cm et dont le volume est un litre. Quelle est sa hauteur ?

Solution : 1 litre = 1000 cm³. S = πR² = (approximativement) 78,54 cm². V = πR² x h.

Donc h = 1000 / 78,54 = 12,7 cm.

 

Exercices

1. Un cylindre droit a pour base un cercle de rayon 1 m, et une surface totale (2 bases + paroi) de 10 m². Quel est son volume ?
2. Considérons une collection de cylindres droits qui ont tous pour surface totale 10 m² (paroi et deux bases). Essayez différents rayons pour trouver celui qui correspond au volume maximal. (Pour les élèves qui savent, utiliser un tableur, et essayer les rayons 1 m, 90cm, 80cm, 70 cm, etc. jusqu'à 10 cm.)

Réponses

 

 

Plan général du cours

Contacter le professeur

 

Réponses

1. Un cylindre droit a pour base un cercle de rayon 1 m, et une surface totale S (2 bases + paroi) de 10 m². Quel est son volume ? Réponse : la surface totale du cylindre est 2 x πR² + 2πR x h = 2 x 3,14 + 6,28 x h = 6,28 x (1 + h). Ça doit être égal à 10. Donc 1 + h = 1,59, et h = 0,59 centimètres. Le volume est V = πR² x h = 3,14 x 0,59 = 1,86 m³.
   
   
2. Considérons une collection de cylindres droits qui ont tous pour surface totale 10 m² (paroi et deux bases). Essayez différents rayons pour trouver celui qui correspond au volume maximal.
   
   Réponse : on va resoudre le problème en essayant, comme l'énoncé le suggère, différents rayons R. (La hauteur h sera chaque fois déterminée. En effet c'est une fonction du rayon puisque la surface totale reste constante.)
   
   En essayant tous les rayons depuis 1 mètre jusqu'à 10 cm (de 10 cm en 10 cm), on obtient le tableau suivant :
   
   
   
   On voit que le volume maximal dans ce tableau est atteint pour R = 70 cm. Un calcul plus précis montrerait que le rayon qui maximise le volume, à surface totale constante 10 m², est environ 73 cm.