Cours de mathématiques de 5e Opérations avec les fractions
Video

Texte

Jusqu'à présent, nous avons travaillé avec les fractions sur la demi-droite des nombres. Elles sont aussi très utiles dans le plan et dans l'espace. Et elles servent encore à beaucoup d'autres choses.

Une fraction exprime une "proportion". 3/4 est la proportion "3 par rapport à 4". On la note aussi 0,75 car c'est un nombre décimal. Et on peut aussi la noter 75%, ça veut dire exactement la même chose.

(Les livres qui, pour dire que B est dans la proportion 75% de A, écrivent (B/A) x 100 = 75%, ont pour auteurs des demeurés. Voir l'exemple d'un célèbre livre de comptabilité au Royaume Uni.)

 

Exemple d'utilisation des fractions. Supposons que j'ai une recette de gâteau pour 4 personnes :
- 4 œufs
- 150 grammes de sucre
- 500 grammes de farine
- 125 grammes de beurre
- un peu de sel et de la levure

Comment modifier mes quantités pour faire un gâteau pour 3 personnes ?

On va prendre la proportion 3/4 de chaque quantité :

 

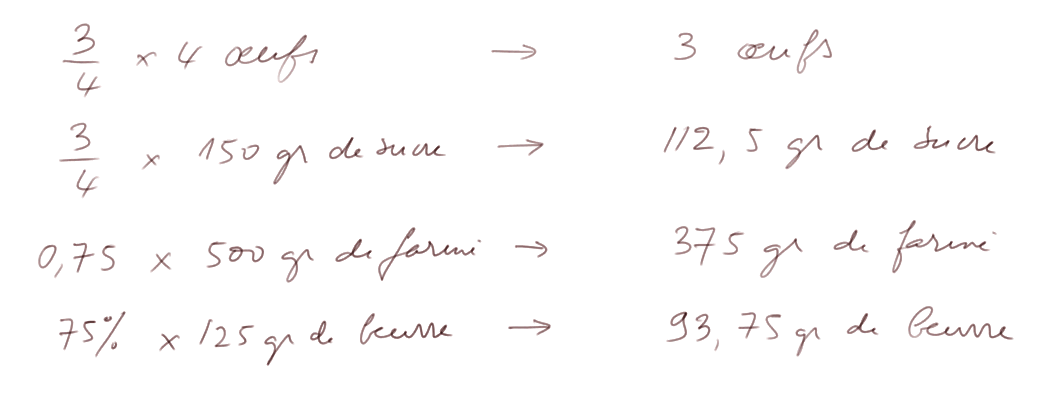
Deuxième exemple : j'ai une pièce de 3 mètres sur 5 mètres. Je veux dessiner le plan d'une autre pièce de telle sorte que
- les deux côtés restent dans la même proportion que pour la première
- le petit côté de la nouvelle pièce fasse 4 mètres.

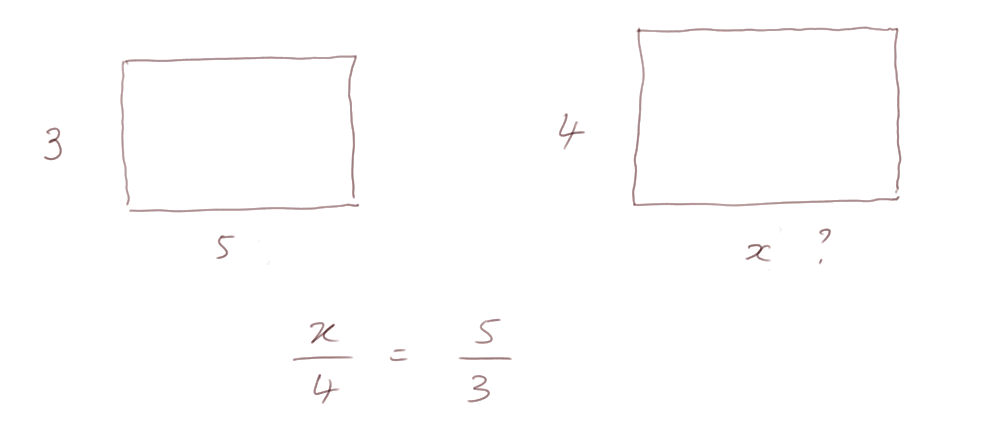
La longueur inconnue, qu'on appelle temporairement x, doit satisfaire la contrainte : x/4 = 5/3

Donc x est 4 fois 5/3. C'est-à-dire x = 4 x 5/3 = 20/3 mètres. (Ce n'est pas un nombre décimal, puisqu'elle est simplifiée au maximum et que 3 n'est pas un diviseur d'une puissance de 10.)

Autre façon de parvenir au même résultat : on veut que le petit côté passe de 3m à 4m, c'est-à-dire qu'on le multiplie par la fraction 4/3. Alors il faut multiplier le grand côté dans la même proportion : donc le nouveau grand côté devient 5 x 4/3 = 20/3.

Supposons maintenant, que je change d'avis et que je veuille que le petit côté fasse 5 mètres. On peut travailler soit avec le rectangle initial, soit avec le nouveau (celui à droite ci-dessus). Le résultat sera le même. Le nouvel x doit être dans la proportion 5/4 du précédent. Donc le nouveau grand côté doit avoir la longueur 5/4 x 20/3 = 100/12 = 50/6 = 25/3. Là non plus ce n'est pas un nombre décimal mais peu importe.

 

 

Troisième exemple. Regardons comment Thalès (c. 625, c. 547 avant J.-C.), à la demande du pharaon Ahmosis II, a mesuré la hauteur de la pyramide de Khéops.

Schématisons le problème avec le dessin ci-dessous.

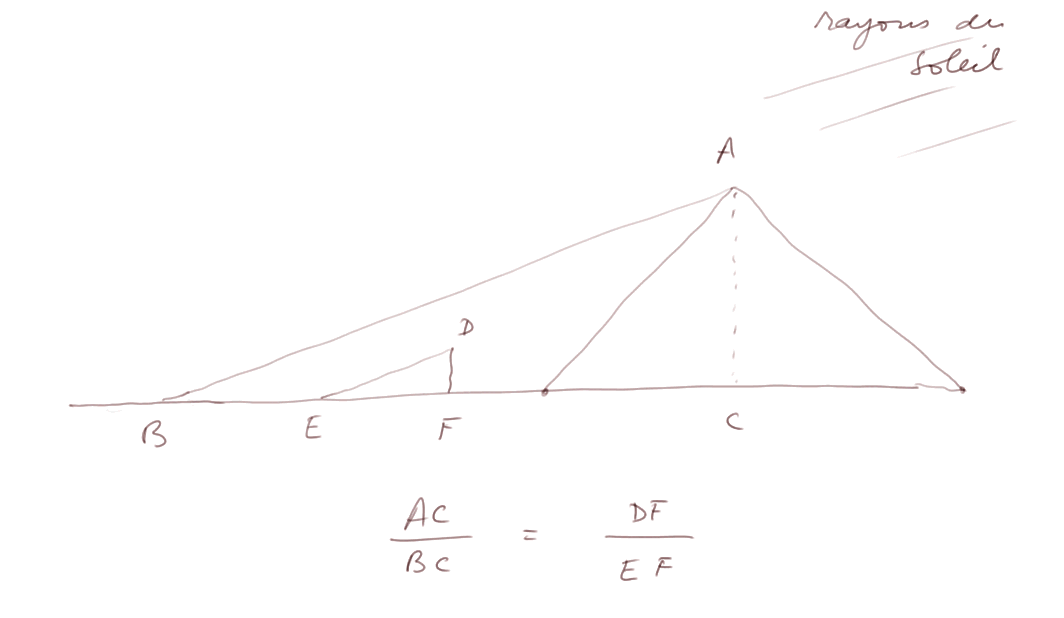
Thalès a astucieusement utilisé les ombres crées par le soleil. Le soleil étant extrêmement éloigné, on peut considérer que ses rayons arrivant sur la Terre sont tous parallèles. L'ombre du sommet de la pyramide (le point A) se projette en B. Et on a un premier triangle dans la figure : le triangle ABC.

Thalès a posé sa canne DF, de 1 mètre de long, à côté de la pyramide. Et il a demandé qu'on mesure la longueur de l'ombre EF, ainsi que la longueur BC. Le point C est facile à connaître puisque c'est le milieu des deux bords de la pyramide.

(Comme tout mathématicien, Thalès était un peu dans la lune, et il a d'abord posé sa canne à l'ombre de la pyramide ! Mais ensuite il s'est déplacé vers nous afin que sa canne soit au soleil.)

Thalès a utilisé un résultat sur les triangles : deux triangles dont tous les côtés sont parallèles deux à deux, ont des longueurs de côtés toutes dans la même proportion. Nous verrons ce résultat de géométrie plus tard. Contentons-nous pour l'instant de l'utiliser.

Les deux triangles dont tous les côtés sont parallèles deux à deux sont ABC et DEF.

Alors on a AC/BC = DF/EF. Thalès a demandé qu'on mesure la longueur de l'ombre de sa canne (EF), et la longueur de l'ombre de la pyramide à partir de son centre, c'est-à-dire BC.

On lui a dit que EF = 3 mètres, et BC = 435 mètres. (Ni les Grecs, ni les Egyptiens, à l'époque, n'utilisaient les mètres, mais je modernise un peu les choses.)

Finalement on a AC/435 = 1/3. Donc AC = 435 x 1/3 = 145 mètres.

 

Exercices

1. Trouver le nombre qui est dans la proportion 13/8 de 50.
2. Les deux fractions 13/8 et 28/17 sont-elles égales ?

Réponses

 

Plan général du cours

Contacter le professeur

 

 

Réponses

1. Trouver le nombre qui est dans la proportion 13/8 de 50. Réponse : 81,25
2. Les deux fractions 13/8 et 28/17 sont-elles égales ? Réponse : non, 13/8 < 28/17