Cours de mathématiques de 2ndeEquations à une inconnue |
|
Video |
Texte
Au sortir du collège, il est fondamental de reconnaître les problèmes de la vie courante qui se transforment en une équation à une inconnue, peut-être du 1er degré, peut-être du 2e, peut-être d'une autre forme. Il faut savoir la résoudre par l'algèbre (quand c'est possible) et par la géométrie. Nous allons faire quelques exercices.
Exercice 1. Soit une quantité inconnue telle que si je prends 2/3 de cette valeur et je rajoute 1, ou si j'en prends les 3/4 et je rajoute 2, j'obtiens le même résultat. Quelle est cette valeur ?
Mise en équation : appelons x cette valeur inconnue. Alors le problème donne la contrainte
Solution par l'algèbre :
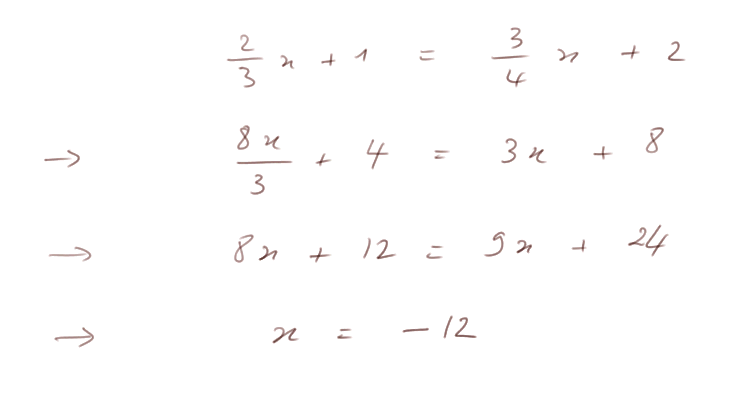
Solution par la géométrie : traçons les deux droites y = (2/3)x + 1 et y = (3/4)x + 2. Le point où elles se couperont aura une abscisse qui vérifiera nécessairement l'équation de l'exercice.
Pour tracer des points de la première droite (en rouge), on observe que pour x = 0, y = l'ordonnée à l'origine = 1. Ensuite chaque fois qu'on se déplace de 3 unités par rapport à l'axe des x, on se déplace (quand on reste sur la droite) de 2 unités par rapport à l'axe des y.
On fait le même genre de construction pour la deuxième droite (en bleu). Le dessin est le suivant
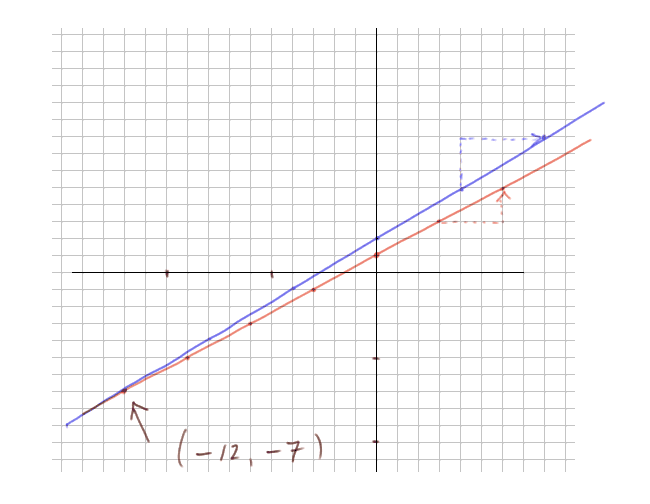
Et le point d'intersection est (-12 ; -7). Car si on se déplace sur la droite rouge, à partir du point (0 ; 1), de quatre fois trois unités vers la gauche on descend aussi de quatre fois deux unités, donc on tombe sur (-12 ; -7). Et si on se déplace sur la droite bleue, à partir du point (0 ; 2), de trois fois quatre unités vers la gauche, on descend en même temps de trois fois trois unités et on tombe encore sur (-12 ; -7).
Exercice 2. Exemple d'équation du 2nd degré se ramenant à une équation du 1er degré :
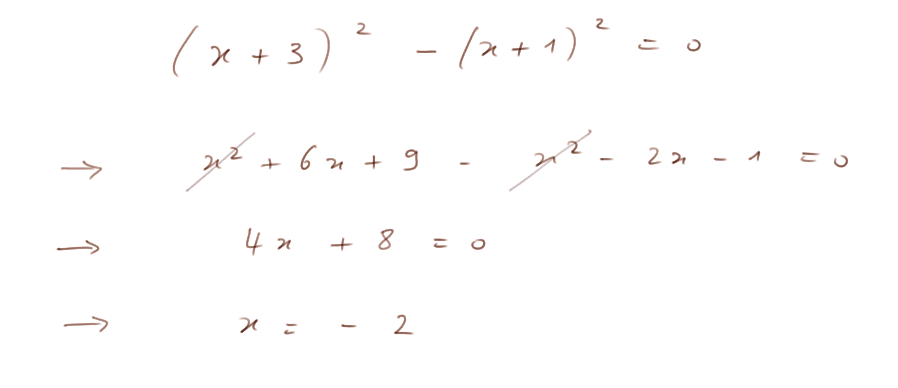
Exercice 3. Equation du 2nd degré (dans cet exemple on va utiliser une identité remarquable, voir vidéo)
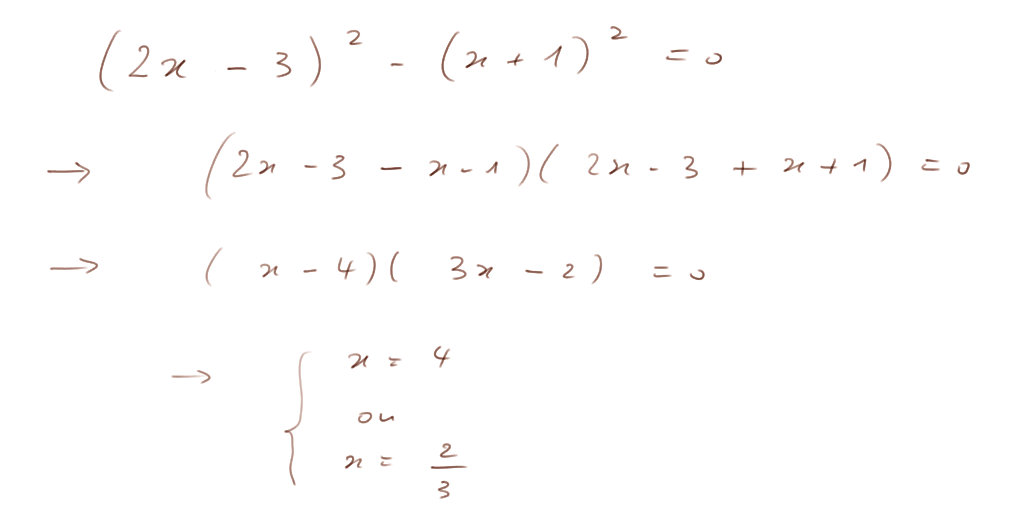
Exercice 4. Il s'agit d'un problème célèbre du Moyen Âge. J'ai un rectangle de côtés a et b
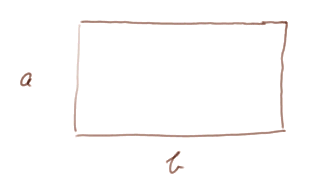
tel que si j'enlève le carré de côté a qui tient dans le rectangle à gauche, j'obtiens un nouveau rectangle (en vert ci-dessous) de même proportion que le rectangle initial.

Quelle est la proportion b/a ?
Mise en équation : on peut écrire b/a = a/(b-a) pour exprimer l'égalité des proportions.
On obtient une équation trinôme, et on la résout selon la formule algébrique qu'on a apprise (il se trouve que son discriminant est positif) :
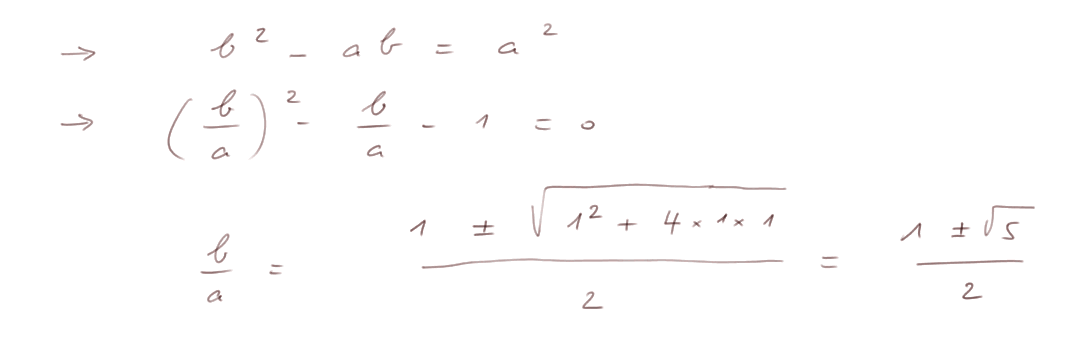
Naturellement la dernière "double égalité" (avec "plus ou moins") est une conséquence nécessaire. Mais ça ne veut pas dire que les deux solutions soient solutions du problème de départ. Il faut aussi que b/a soit positif.
Donc la solution est
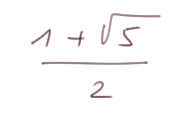
Les mathématiciens du Moyen Âge appelaient ce nombre, "le nombre d'or".
Ils trouvaient que c'était "la plus belle proportion" pour un rectangle, et beaucoup de palais italiens construits à la Renaissance ont des fenêtres avec cette proportion. Selon les goûts modernes elle est un peu trop allongée.
Suite de Fibonacci, alias Léonard de Pise (c. 1175, c. 1250)
C'est la suite de nombres obtenue en partant des deux premiers nombres 1 et 1, puis chaque nombre suivant est la somme des deux précédents :
1 1 2 3 5 8 11 etc.
D'une manière générale si on appelle un le n-ième nombre, on a un+1 = un + un-1
Alors on verra dans un cours ultérieur que le ratio un+1 / un tend vers le nombre d'or.
Exercices :
- Vérifier expérimentalement que dans la suite de Fibonacci, un+1 / un se rapproche effectivement de plus en plus de (1 + √5) / 2.