Cours de mathématiques de 2nde Fonctions usuelles, et fonctions inverses
Video

Texte

Nous avons déjà appris un certain nombre de fonctions dites "usuelles" :

1. fonction "carrée". C'est la fonction f qui a x associe f(x) = x²
2. fonction "racine carrée". A x est associé √x. Evidemment, cette fonction n'est pas définie partout. On va réviser où.
3. fonction "1 sur x". A x est associé 1/x.
4. fonction "cube". A x est associé x³.
5. fonction "valeur absolue". A x est associé |x|, c'est-à-dire, on se rappelle x, si x est positif ou nul, et -x si x est négatif.

Nous en apprendrons quelques autres dans les années qui viennent. Par exemple :

• les fonctions "trigonométriques" : sin(x), cos(x), tan(x), etc. Nous les apprendrons cette année dans quelques leçons.
• la fonction "exponentielle". A x est associé e^x. On a déjà un peu étudié les puissances d'un nombre en 4e. Ici il s'agira d'un nombre particulier "e" (= 2,718 281 828 459...) aussi important que Π (= 3,141 596 535 897...), pour des raisons qu'on verra.
• la fonction "logarithme". A x est associé log(x).

Revenons à celles que nous connaissons déjà. Dans chaque cas il est important de

• savoir sur quelle région de R elle est définie
• savoir la tracer
• et donc savoir, en particulier, là où elle croît et là où elle décroît.

 

Fonction "carrée". Le dessin de cette fonction est ce qu'on appelle une parabole.

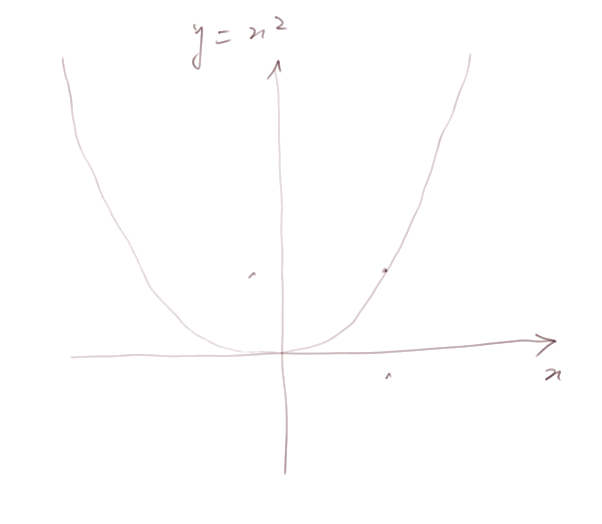
L'étude de son sens de variation est :

Quand x est entre moins l'infini et zéro, la fonction décroît, et quand x est entre zéro et plus l'infini, la fonction croît. La courbe a deux branches symétriques par rapport à l'axe vertical des y. Sur R+ la courbe (c'est-à-dire la fonction) croît de plus en plus vite.

 

Fonction "1 sur x". Elle est définie sur tout R sauf pour x = 0. Le dessin de cette fonction est ce qu'on appelle une hyperbole.

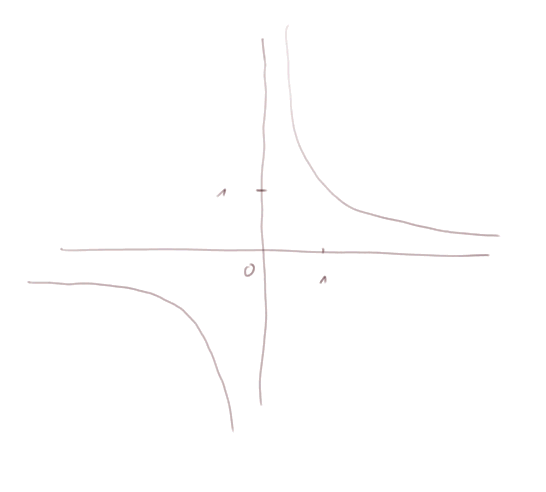
Sens de variation :

 

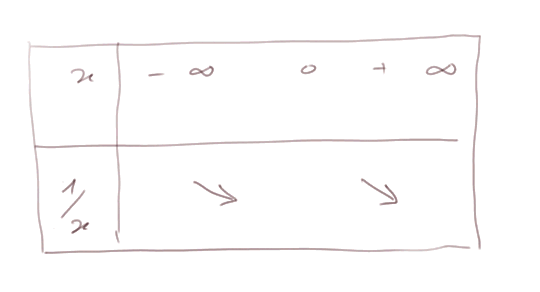
Fonction "racine carrée". Elle est définie seulement pour x ≥ 0.

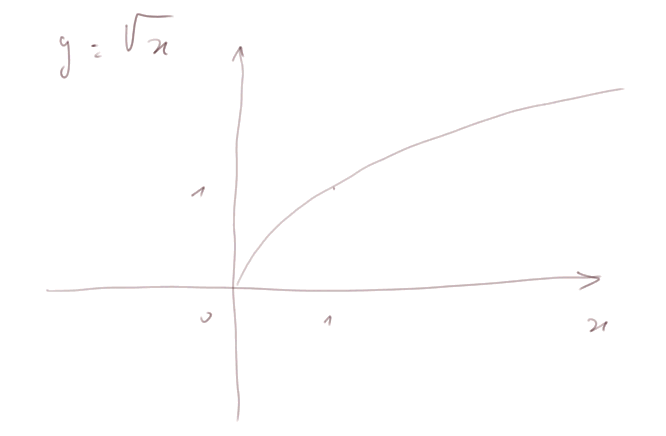
Elle est croissante, mais croît de plus en plus lentement.

 

Fonction "cube". Définie sur tout R.

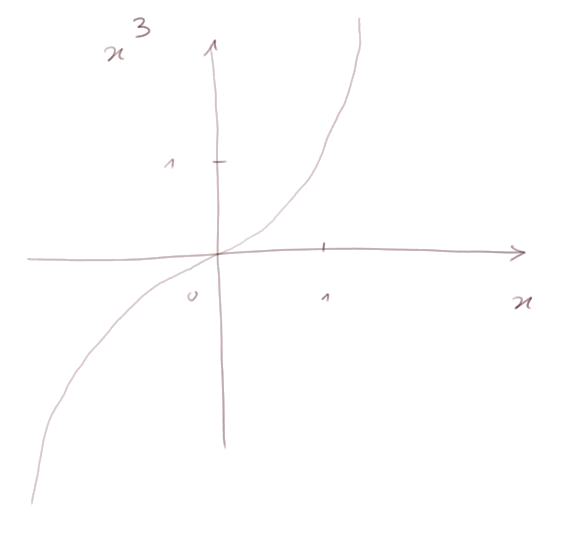
croissante.

 

Fonction "valeur absolue". Définie sur tout R.

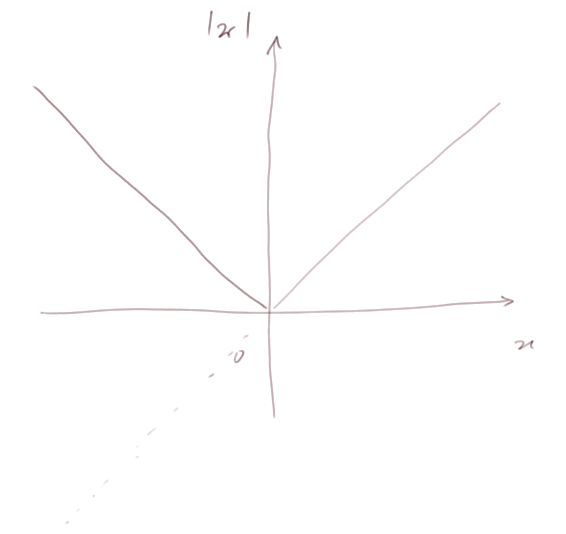
Sens de variation

 

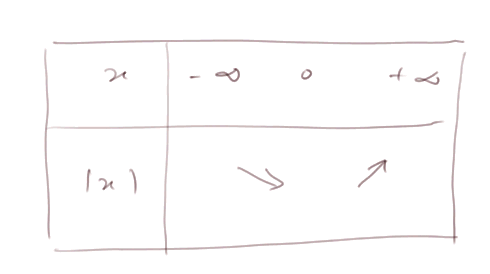
Après ces petites révisions, abordons un concept important dans les fonctions : les fonctions inverses.

Fonctions inverses.

Le terme "fonction inverse" est utilisé dans deux sens différents :

1. pour nommer la fonction qui à x associe 1/x
2. pour nommer la fonction (quand elle existe) notée f^-1 qui combinée à f redonne la valeur x initiale :
   f^-1 ○ f (x) = x
   

Dans ce cours, le terme "fonction inverse" est réservé au deuxième sens.

 

Quand f^-1 existe-t-elle ?

Soit une fonction f définie sur un segment [a, b], telle que tous les points de [a, b] soient projetés dans un segment [α, β] (où les bornes ne sont pas nécessairement projetées sur les bornes). Si à chaque y dans [α, β] correspond un seul x dans [a, b] tel que y = f(x), alors par définition la fonction f^-1 est une fonction de [α, β] vers [a, b], et

x = f^-1(y)

 

Exemple et contre-exemple (1) :

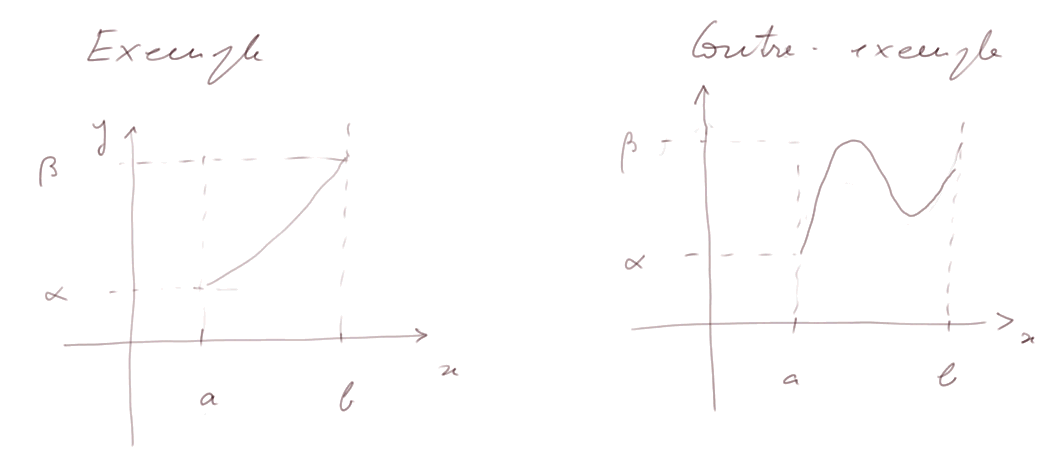
A gauche, la propriété permettant de définir f^-1 est satisfaite : à chaque y ne correspond qu'un seul x tel que y = f(x). Mais à droite ce n'est pas le cas.

 

Exemple et contre-exemple (2) :

 

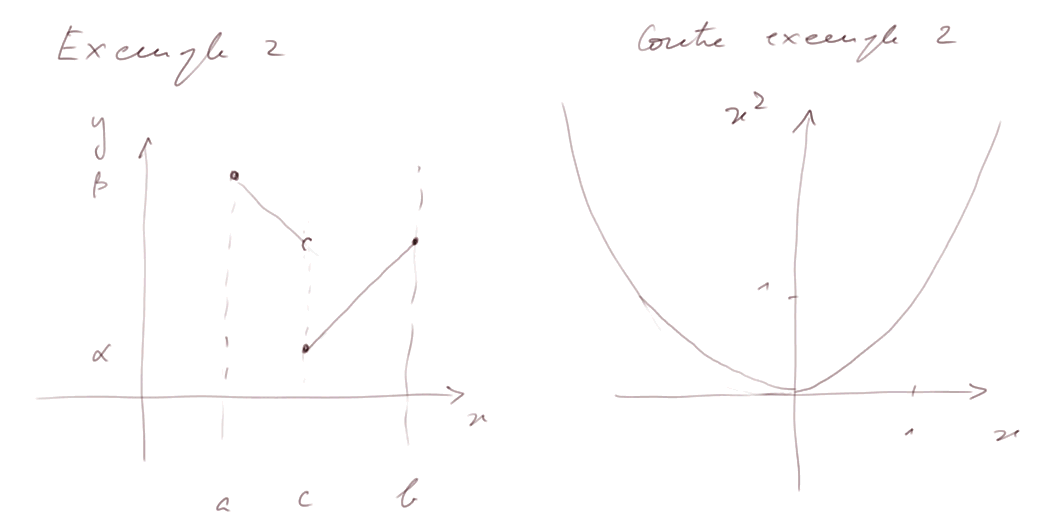
Dans l'exemple de gauche, on a pris une fonction "un peu bizarre", mais elle satisfait la condition pour que f^-1 existe. Tandis que y = x² prise sur tout R ne la satisfait pas.

 

y = x² considérée seulement sur tout R+. Dans ce cas la condition pour que f^-1 existe est satisfaite.

 

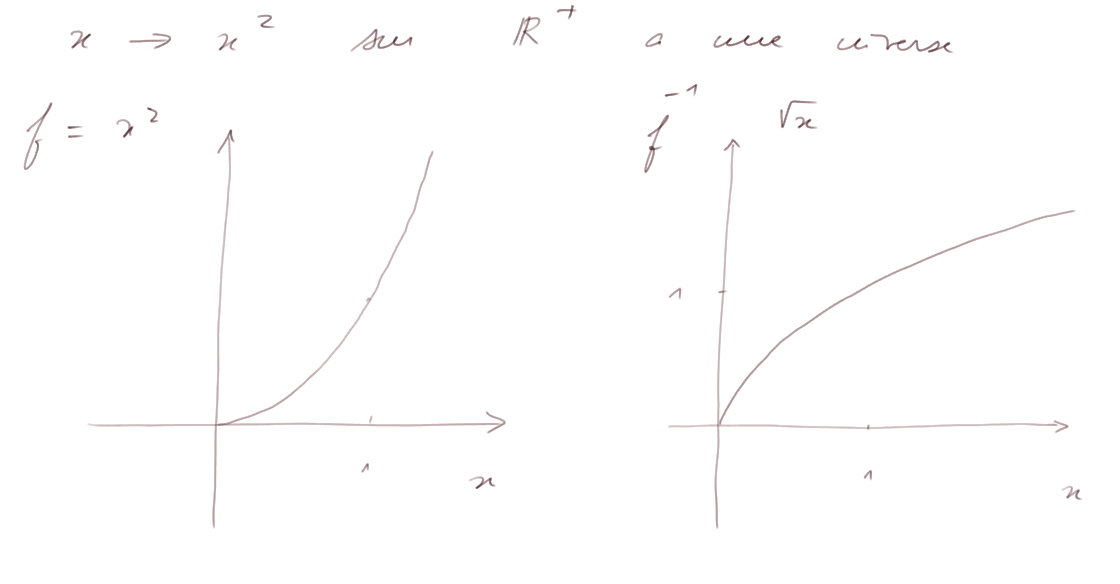
Comment obtenir la courbe de f^-1. Quand f^-1 existe, sa courbe est simplement la symétrique de la courbe de f par rapport à la droite bissectrice du premier quadrant du plan.

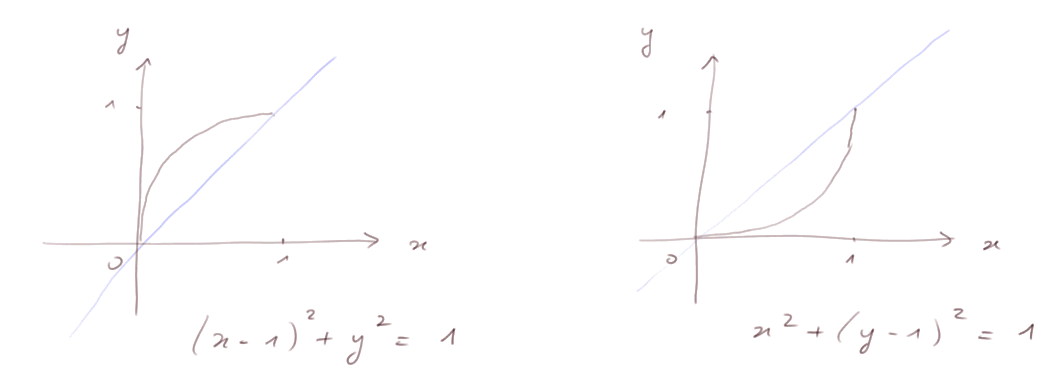
Dans l'exemple ci-dessus, nous avons pris la courbe d'un arc de cercle (centré en (1 ; 0) et de rayon 1).

 

Exercices :

1. Soit l'hyperbole y = 1/x ci-dessous, et une abscisse p quelconque sur ] 0 ; +∞ [.
   
   
   Au point P, la pente de la droite bleue (tangente à l'hyperbole) est -1/p². Montrer que la surface du triangle vert est constante quel que soit le nombre p initial.
   
   
2. Soit la parabole y = x² ci-dessous.
   
   
   En découpant la surface sous la courbe entre 0 et 1 comme sur la figure, avec un découpage de plus en plus fin, montrer que la surface sous la courbe entre 0 et 1 est 1/3.
   
   Conseil : découper [0, 1] en n parties égales. Utiliser la formule
   
   1² + 2² + 3² + 4² + 5² + ... + m² = m(m+1)(2m+1)/6
   
   avec m = n-1.
   
   
   

 

Plan général du cours

Contacter le professeur