Cours de mathématiques de 2nde Voisinages et approximations
Video

Texte

Il s'agit de la formalisation de l'idée intuitive de proximité d'un nombre ou d'un point.

Voisinage de x. Soit un nombre réel x, ou, de manière équivalente, un point quelconque sur la droite de représentation des nombres. Un voisinage de x, c'est un petit segment autour de x. Exemple : [ x - ε, x + ε ], où ε est un petit nombre (prononcer "epsilon", en faisant sonner le "...on" comme dans "sonne").

Evidemment, cette définition d'un point de vue mathématique est vague. Qu'est-ce qu'un petit nombre ? Les enfants vers 5 ans demandent parfois en écartant les mains d'une trentaine de centimètres : "Dis papa, est-ce que ça c'est grand ou petit ?" Très difficile de répondre... :-)

Mais d'un point de vue intuitif, c'est clair. Voici un exemple :

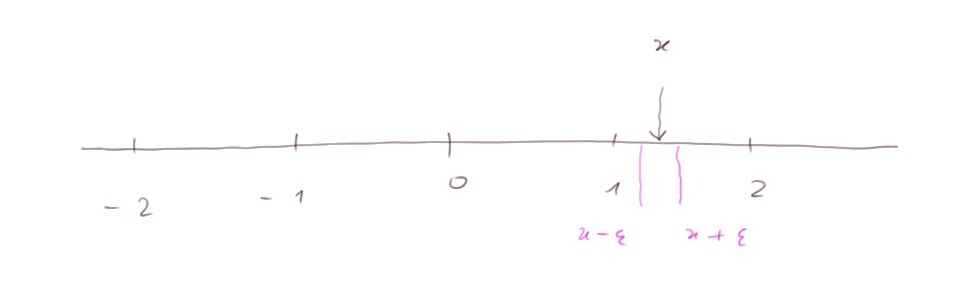
Ici x = 1,3 et ε = 0,1. Eh bien, [ 1,2 ; 1,4 ] est un voisinage de 1,3.

Les débordements à gauche et à droite n'ont pas besoin d'être égaux. ] x - ε, x + η [ où ε et η (prononcer "éta") sont "petits" est aussi un voisinage de x. J'ai pris un segment ouvert. C'est plus habituel en mathématiques avancées, pour des raisons qu'on verra plus tard.

 

Approximation de x. Une approximation de x est un nombre proche de x, c'est-à-dire un nombre dans un voisinage de x.

Exemple : 3,162 est une approximation de √10, car 3,16 < √10 < 3,17.

En effet (3,16)² = 9,9856 (exactement) et (3,17)² = 10,0489 (exactement), et la fonction f : x -> f(x) = x² est strictement croissante pour les x ≥ 0.

Par là, on veut dire que si 0 ≤ x₁ < x₂, alors f(x₁) < f(x₂) .

 

Précision d'une approximation. Soit un nombre x et une approximation x₁ de x. Si | x - x₁ | ≤ ε, on dit que x₁ est une approximation de x "à ε près".

Exemple, 3,16 est une approximation de √10 au centième près, car | 3,16 - √10 | ≤ 1/100.

3,17 est aussi une approximation au centième de √10.

3,165 aussi, etc.

 

Une propriété simple :

Si x₁ approxime x à ε près, et y₁ approxime y à η près, alors x₁ + y₁ approxime x + y à ε + η près. C'est une évidence géométrique : x₁ + y₁ est au maximum à la distance ε + η de x + y.

 

Les notions de voisinage et d'approximation peuvent apparaître comme des raffinements consistant à couper les cheveux en quatre, ce qu'on appelle aussi de "l'epsilonite". Mais il faut noter qu'avec les calculettes et les ordinateurs on travaille le plus souvent avec des approximations :

0,333 est une approximation au millième de 1/3, car | 0,333 - 1/3 | ≤ 1/(10³)

 

On se rappelle que si | a | < 1, alors

En particulier, on a l'identité exacte (pour a ≠ 1) :

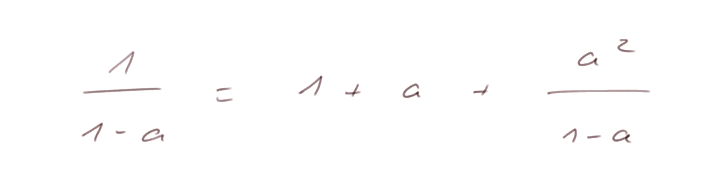
Si "a" est petit, alors a² est "très petit" (par exemple si a = 1/100, alors a²= 1/10000). Donc, si "a" est petit, (1 + a) est une bonne approximation de 1 / (1 - a).

Prenons un exemple avec | a | < 1/10. Dans ce cas,

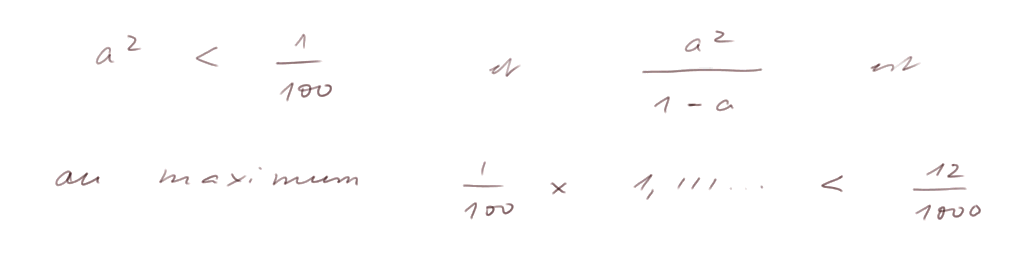
Donc

 

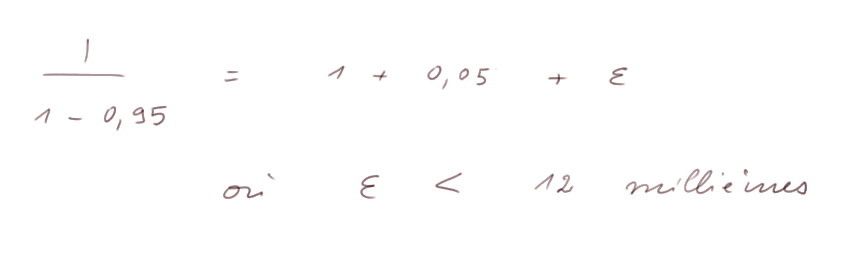
Suite de voisinages de plus en plus serrés. On sera amené à regarder une collection de voisinages autour de x, de plus en plus serrés :

v₁, v₂, v₃, ... v_n, ... tels que ∀ ε, en allant suffisamment loin avec n, tous les v_m encore plus loin ont une largeur plus petite que ε.

 

Par exemple, on s'intéressera aux fonctions f telles que si une suite de x_n sont dans des voisinages v_n de x, et la collection v₁, v₂, v₃, ... v_n, ... est de plus en plus serrée, alors les f(x_n) sont dans des voisinages w_n de y = f(x), et les w_n sont de plus en plus serrés.

C'est une façon précise d'exprimer l'idée simple suivante : pour certaines fonctions f, quand x s'approche d'un nombre "a", f(x) s'approche de f(a).

C'est le cas de toutes les fonctions qu'on a rencontrées jusqu'à présent, par exemple

• x -> 2x + 3
• x -> x²

Mais on rencontrera des fonctions naturelles où ce n'est pas le cas partout. Par exemple, quand nous étudierons un peu plus la fonction sinus, on verra que sin(1/x) ne vérifie pas cette propriété pour x = 0. "Normal, direz-vous, sin(1/0) n'est pas défini.
- Exact, mais même si on se rapproche autant qu'on veut de zéro (sans l'atteindre), sin(1/x) continue à s'agiter sans se resserer."

 

Exercices :

1. Démontrer l'identité exacte (pour a ≠ 1)
   
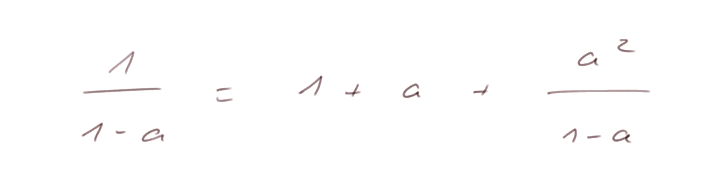
2. Pour "a" petit, pouvez-vous penser à une approximation de [ 1 / (1 - a) ] encore bien meilleure que (1 + a) ?
3. Prouver que si | a | < 1, alors
   
   où la suite infinie à droite veut seulement dire "en allant suffisamment loin avec n, on peut rendre la somme finie 1 + a + a² + a³ + ... + aⁿ aussi proche qu'on veut du terme de gauche". (Suggestion : utiliser une identité exacte du même genre que celle de l'exercice 1, mais avec 1 + a + a² + a³ + ... + aⁿ et un reste dont on trouvera la forme exacte.)
   
   
   

 

Plan général du cours

Contacter le professeur