Cours de mathématiques de 3eDéveloppements algébriques |
|
|
|
|
Video |
|
Texte
On a déjà rencontré (a + b)2 = a2 + 2ab + b2. Il s'agit d'une application de la distributivité de la multiplication sur l'addition : (a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2.
Cette identité est toujours vraie, quels que soient les nombres réels a et b. Essayons avec a = 2 et b = 7. D'une part (2 + 7)2 = 9 x 9 = 81. D'autre part, d'après l'identité ci-dessus, ça doit être égal à 22 + 2 x 2 x 7 + 72 = 4 + 28 + 49 = 31 + 50 = 81. Donc c'est vérifié.
Cette identité a une interprétation géométrique :
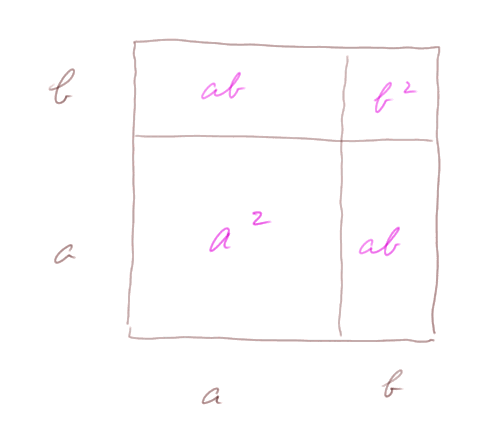
On voit que le grand carré, qui a pour surface (a + b)2, a aussi pour surface a2 + ab + ab + b2 = a2 + 2ab + b2.
De même, on a l'identité (a - b)2 = a2 - 2ab + b2. Interprétation géométrique :
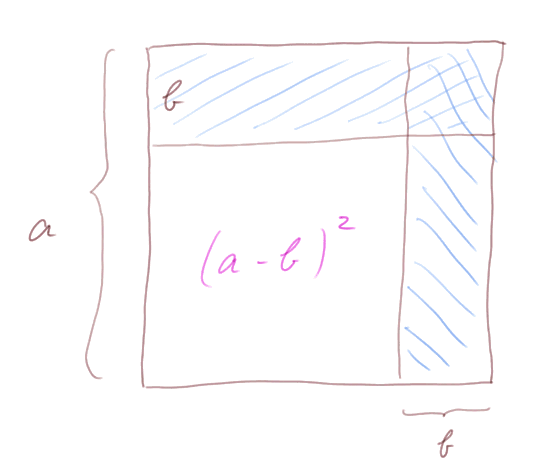
Cette fois, on part d'un grand carré de côté a, et on diminue chaque côté de la longueur b. La surface (a - b)2 peut être obtenue en partant de la surface totale a2 à laquelle on enlève deux fois les rectangles bleutés (qui ont pour surface ab), mais alors on a enlevé le petit carré (de surface b2) une fois de trop, donc il faut le rajouter. D'où (a - b)2 = a2 - 2ab + b2.
On a aussi : (a + b)(a - b) = a2 - b2. Comme dans les autres cas, il y a trente-six façons de le démontrer. Regardons une interprétation géométrique :
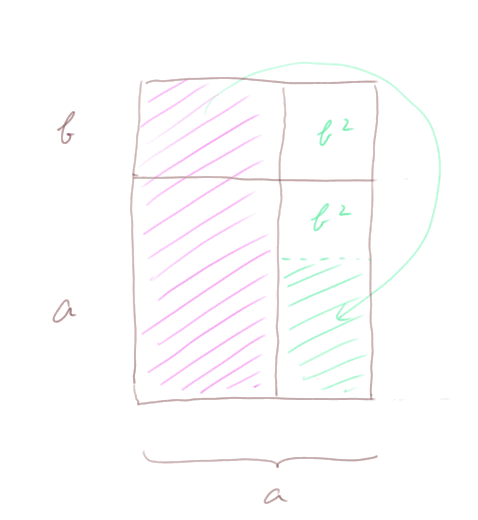
On part du rectangle de côtés a et (a + b). Le rectangle rose a pour surface (a + b)(a - b). Comme le petit rectangle rose en haut tient dans le rectangle à droite et il reste encore b2, on a donc (a + b)(a - b) = a2 - b2.
On a aussi déjà rencontré l'identité: (a - 1)(an + an-1 + an-2 + ... + a2 + a + 1) = an+1 - 1. Il suffit de développer le terme de gauche pour voir que tous les termes vont s'annuler sauf deux. Ce sont ceux qui sont notés à droite.
Par conséquent, si a est différent de 1, on a aussi : 1 + a + a2 + ... + an-1 + an = (an+1 - 1) / (a - 1) = (1 - an+1) / (1 - a).
Si on remplace a par -a, et que a est maintenant différent de -1, on obtient : 1 - a + a2 - ... + (-a)n = (1 + (-a)n+1) / (1 + a).
Pour finir, regardons une approximation aussi simple qu'utile et un peu surprenante tellement elle marche bien. On part de (1 - a)(1 + a) = 1 - a2 qui est toujours vraie. Alors si a est "petit", on a (1 - a)(1 + a) ≈ 1.
D'où, si a est "petit", (1 - a) ≈ 1 / (1 + a).
Essayons avec a = 5%.
Avec une calculette, on vérifie que 1/(1 + 5%) = 0,9523... Ce n'est pas très différent de 1 - 5%.
Exercices :
- Faire le même calcul que ci-dessus, avec a = 5%, mais en utilisant la formule 1 - a + a2 pour approximer 1 / (1 + a). Vérifier qu'elle est encore beaucoup plus précise que (1 - a).