Cours de mathématiques de 3eGéométrie analytique (1) : pratique avec les droites |
|
Video |
Texte
La géométrie analytique est la résolution de problèmes de géométrie à l'aide de l'algèbre. Parfois des problèmes de géométrie, une fois différents points de la figure repérés par leurs coordonnées, deviennent plus faciles à résoudre par l'algèbre. Nous verrons un exemple dans la leçon suivante.
Nous devons tout d'abord devenir très à l'aise avec les équations du 1er degré avec deux variables, ax + by + c = 0, et les droites correspondantes dessinées dans le plan avec un repère. Dans cette leçon nous allons apprendre deux techniques de base. Il est très important de bien les maîtriser, et pour cela il n'y a qu'une façon de faire : beaucoup d'exercices.
On a vu les équations de droites sous la forme y = ax + b, mais il est parfois préférable de travailler avec la forme ax + by + c = 0 *, car la première forme correspond à toutes les droites du plan, sauf les droites verticales.
(* attention : pour une même droite, les coefficients ne sont pas les mêmes d'une forme à l'autre)
Evidemment, si b ≠ 0, ax + by + c = 0 est équivalent à
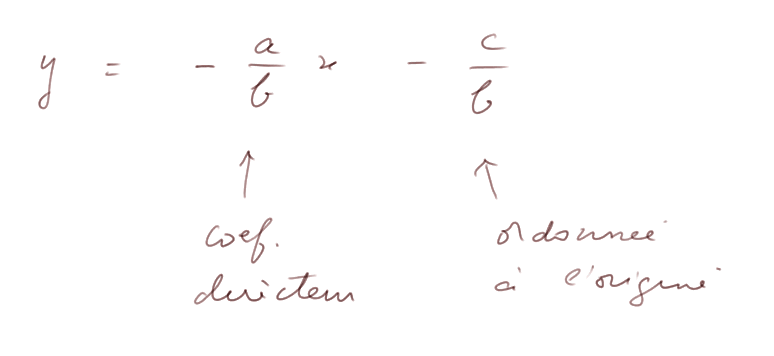
Première technique à maîtriser : Tracer une droite dont on connaît l'équation. Prenons un exemple numérique : tracer la droite formée par l'ensemble des points (x ; y) tels que 2x - 5y + 3 = 0. Ici on peut, si on préfère, revenir à la forme plus habituelle :
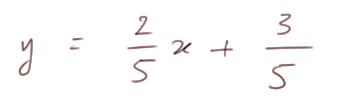
Quand x = 0, l'ordonnée du point sur la droite a pour valeur "l'ordonnée à l'origine", c'est-à-dire 3/5. Et on vérifie aussi aisément que si y = 0, alors l'abcisse du point correspondant sur la droite est x = -3/2. Nous voilà avec deux points, donc on peut tracer la droite :
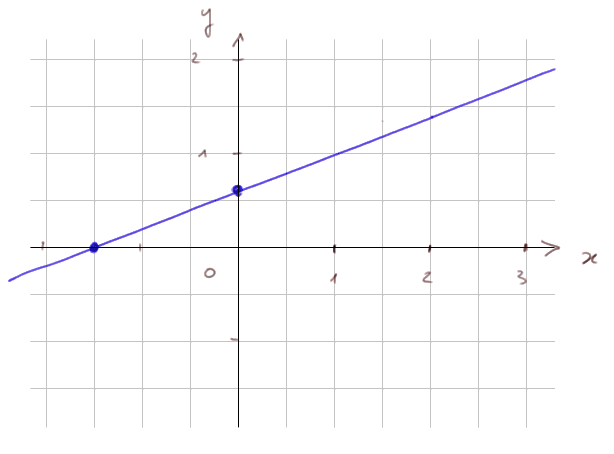
Deuxième technique à maîtriser : Trouver l'équation d'une droite quand on connaît deux points sur celle-ci. Prenons de nouveau un exemple numérique : soit les points (5 ; 2) et (-8 ; 3) dans le plan. Quelle est l'équation de la droite qui passe par ces deux points ?
On va utiliser l'équation de la forme y = ax + b, car ici la droite n'est manifestement pas verticale, et on va trouver des contraintes sur les deux coefficients a et b.
Comme la droite (appelons-la D) doit passer par (5 ; 2), ça nous donne la contrainte 2 = 5a + b. De même comme D passe par (-8 ; 3), on a aussi la contrainte 3 = -8a + b.
Ainsi, on arrive à un système de deux équations linéaires à deux inconnues. Ici les inconnues sont les coefficients a et b :
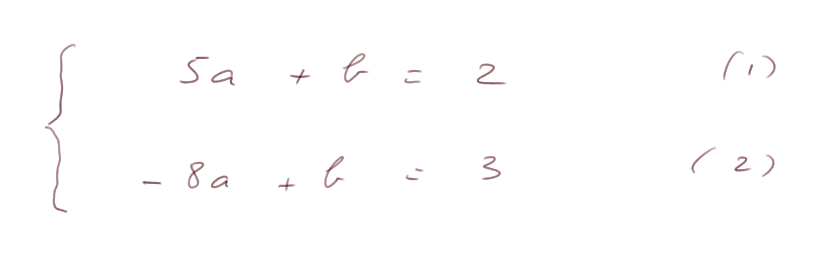
On va résoudre ce système par l'algèbre. L'équation (1) donne b = 2 - 5a. On remplace cette valeur de b dans l'équation (2), et on obtient une équation avec une seule inconnue, le paramètre "a" :
→ -8a + 2 - 5a = 3
→ -13a = 1
→ a = -1/13.
Ensuite, on termine en calculant "b", par exemple avec l'équation (1) :
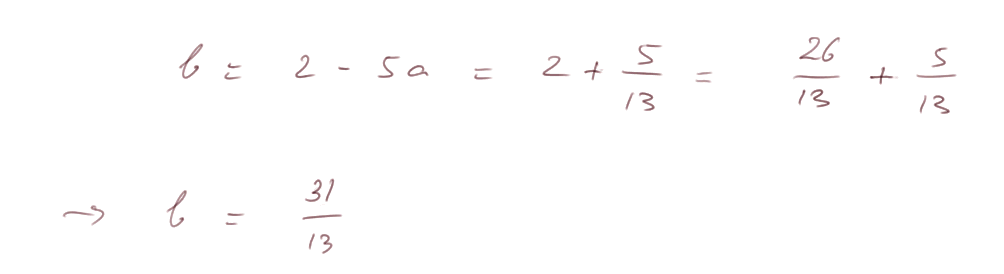
et l'équation finale est
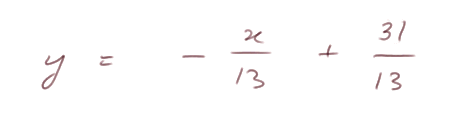
ou, si l'on préfère, x + 13y - 31 = 0.
(L'équation d'une droite peut toujours être multipliée par n'importe quel nombre non nul.)
Vérification : Soit D la droite d'équation x + 13y - 31 = 0.
Est-ce que le point (5 ; 2) est dessus ? Réponse : oui, car 5 + (2 fois 13) - 31 est bien égal à zéro.
Est-ce que le point (-8 ; 3) est dessus ? Réponse : oui car -8 + (3 fois 13) - 31 est aussi égal à zéro.
Exercices :
- Produire et résoudre beaucoup d'exercices mettant en œuvre chacune des deux techniques exposées ci-dessus.