Cours de mathématiques de 3eGéométrie analytique (2) : exemple de résolution de problème |
|
Video |
Texte
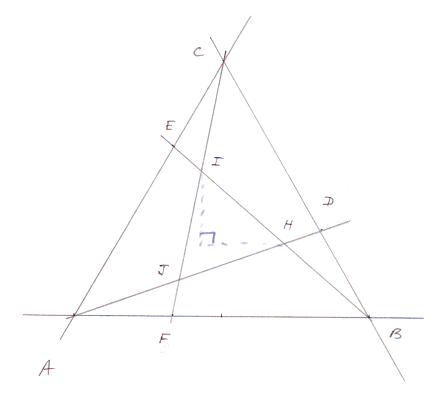
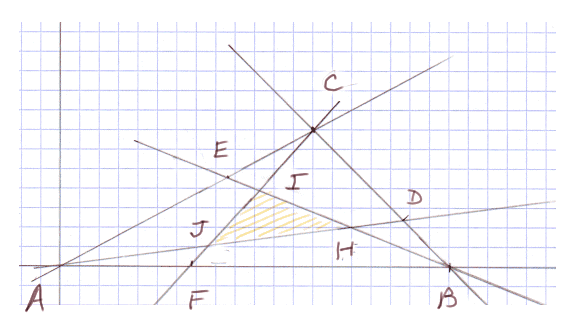
Nous allons étudier un problème de géométrie, difficile à résoudre par la géométrie pure, mais facile par la géométrie analytique. Soit un triangle équilatéral ABC, et les trois droites AD, BE et CF qui coupent les côtés opposés au tiers :
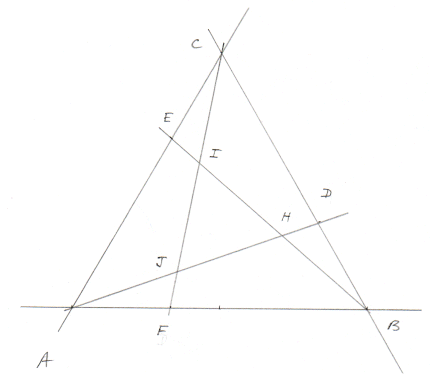
Les intersections des trois droites AD, BE et CF sont nommées H, I et J.
Théorème : le triangle HIJ a pour surface 1/7 de celle de ABC.
Nous allons démontrer ce résultat par la géométrie analytique, c'est-à-dire par l'étude des coordonnées algébriques des différents points de la figure dans un repère. Puis nous généraliserons à un triangle ABC quelconque - car ce résultat est vrai en réalité pour un triangle ABC quelconque - par de la géométrie pure.
Imaginons un repère dans le plan, dont l'origine est le point A, et l'axe des x est la droite AB. Prenons, sans perdre de généralité, la longueur AB comme étant l'unité.
1) Coordonnées de A, B et C : les coordonnées de A, B et C sont :
- A = (0 ; 0)
- B = (1 ; 0)
- C = (1/2 ; (√3)/2)
Pour ceux qui ne se rappelleraient plus la hauteur d'un triangle équilatéral, soit h cette hauteur, alors par Pythagore appliqué au triangle rectangle obtenu en coupant le triangle équilatéral verticalement en son milieu, on a h2 + (1/2)2 = 12.
→ h2 = 3/4
→ h = (√3)/2
2) Coordonnées de D, E et F : Tournons-nous maintenant vers les coordonnées de D, E et F.
Coordonnées de F = (1/3 ; 0)
Coordonnées de D : en abscisse, (par Thalès) D a reculé de 1/3 par rapport à la moitié de BA, donc abscisse = 5/6. Et en ordonnée, (toujours par Thalès) D est à un tiers de celle de C, donc ordonnée = (√3)/6
D = (5/6 ; (√3)/6)
De même E = (1/3 ; 2/3 fois (√3)/2) = (1/3 ; 1/√3)
3) Coordonnées de H, I et J :
Pour calculer les coordonnées de H, on va utiliser ce qu'on a appris dans la leçon précédente sur les droites en géométrie analytique. On va :
- calculer les équations des droites AD et BE, puis
- calculer les coordonnées de leur intersection
Droite AD : elle passe par l'origine, donc son équation est de la forme y = ax. Et elle passe par D (5/6 ; (√3)/6), donc ça nous donne une contrainte sur "a" :
(√3)/6 = a fois 5/6. D'où a = (√3)/5 et l'équation de AD est y = (√3)/5 fois x.
Droite BE : son équation est de la forme y = cx + d. Comme elle passe par B, on a 0 = c + d. Et comme elle passe par E, on a 1/(√3) = c/3 + d.
D'où 1/√3 = -(2/3)c
→ c = -(√3)/2 et d = (√3)/2
Coordonnées du point H : il est sur les deux droites
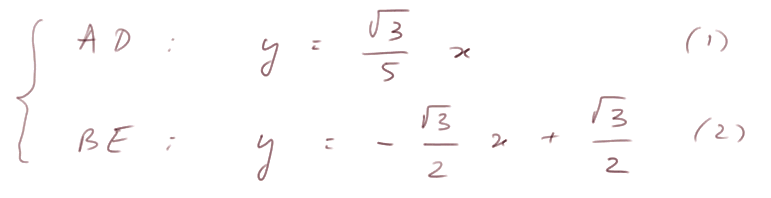
C'est un système de deux équations linéaires à deux inconnues. On le résout comme on a appris : on remplace, dans (2), y par sa valeur exprimée à l'aide de x, donnée par (1)
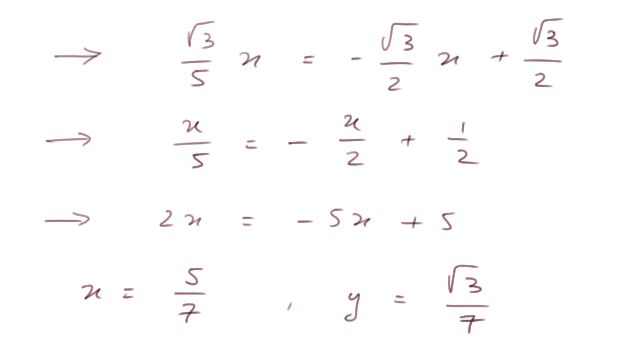
Maintenant on se tourne vers la droite CF et les points I et J.
Droite CF : on a les coordonnées des points C et F
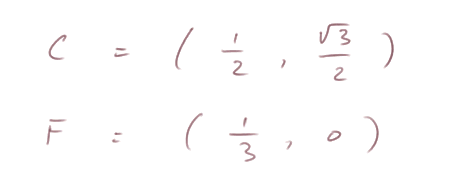
sans rentrer dans les calculs du même type que plus haut, on obtient l'équation de la droite CF : y = (3√3) x - √3.
On peut d'ailleurs vérifier que les deux points C et F sont dessus et que c'est donc forcément la bonne équation. Si x = 1/3, alors y = 0, donc F est dessus. Et si x = 1/2, alors y = (√3)/2, donc C est dessus.
Coordonnées du point J : il est à l'intersection de AD et CF. On obtient le système d'équations linéaires à deux inconnues
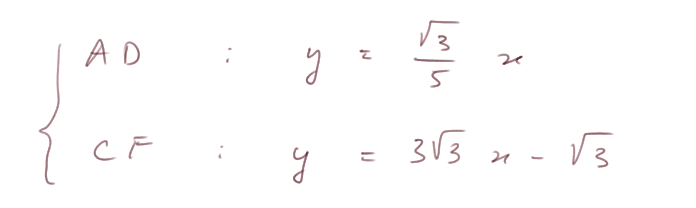
D'où l'on tire, coordonnées de J = (5/14 ; (√3)/14).
Coordonnées du point I : intersection de BE et CF →
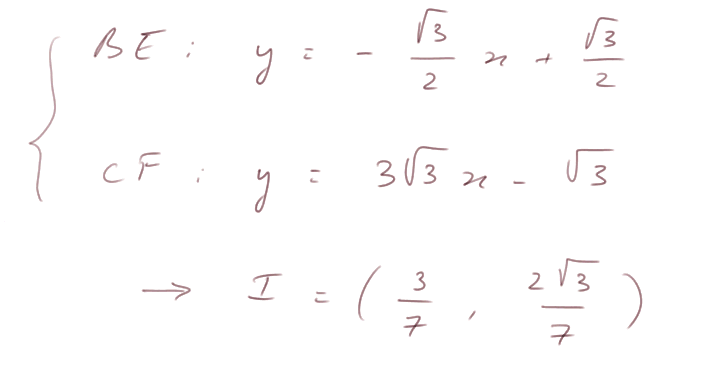
Récapitulation des coordonnées de H, I et J :
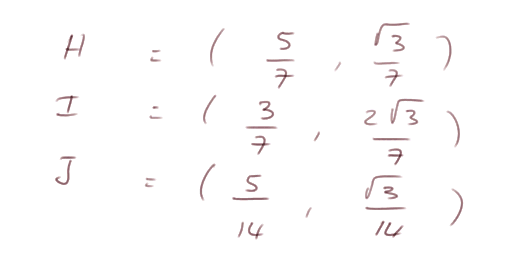
Calcul de la distance HI : d'une manière générale, à l'aide de la géométrie analytique, la distance entre deux points quelconques H et I, de coordonnées (x1 ; y1) et (x2 ; y2), est calculée en utilisant le théorème de Pythagore
(distance HI)2 = (x1 - x2)2 + (y1 - y2)2
Appliqué aux points H et I spécifiques de notre problème, cela donne
(distance HI)2 = (5/7 - 3/7)2 + ((√3)/7 - 2(√3)/7)2 = 4/49 + 3/49 = 1/7.
Donc distance HI = 1/√7.
Comme toute la figure est invariante par rotation de 120° autour du centre, c'est vrai aussi des distances IJ, et JH.
Bref, le petit triangle HIJ est obtenu en multipliant toutes ses dimensions par 1/√7 par rapport à celles de ABC.
Donc sa surface est dans le carré de ce rapport : surface de HIJ = 1/7 x surface de ABC.
Finalement, passons à un triangle quelconque : Dans un triangle ABC quelconque, le résultat est encore vrai.
On s'appuie sur un résultat de géométrie dans l'espace facile à prouver mais que nous ne prouverons pas ici : un triangle quelconque peut toujours être obtenu par projection cylindrique d'un triangle équilatéral sur un autre plan, avec un axe de projection bien choisi. Les alignements et rapport de dimensions et de surfaces sont préservés d'un triangle à l'autre.
Une autre façon de se convaincre du résultat est la suivante :
- on part du triangle ABC équilatéral et on fait glisser C horizontalement vers un point quelconque C' : toutes les surfaces restent les mêmes
- puis on abaisse le point C' verticalement vers un point quelconque C'': toutes les surfaces sont réduites dans la même proportion
- on peut ainsi produire un triangle ABC'' quelconque
- donc la surface de HIJ reste toujours dans la même proportion de celle de ABC, c'est-à-dire 1/7.
Exercices :
- Utiliser le calculateur de triangles en ligne offert par ce site https://www.analyzemath.com/Geometry_calculators/area_triangle_lines.html pour vérifier le théorème avec un triangle quelconque non équilatéral ni isocèle de votre choix.
- Nécessite un niveau 1ere ou terminale : démontrer le résultat de cette leçon en utilisant les coordonnées barycentriques (voir https://math.stackexchange.com/questions/3060573/prove-triangle-area-formula-for-barycentric-coordinates).