Cours de mathématiques de 3eSystème à base dix et système binaire |
|
Video |
Texte
On a une grande familiarité avec le système indo-arabe de notation des nombres. Ce système est dit "positionnel" et "décimal", ou "à base dix"; "positionnel" car un même chiffre signifie qqc de différent selon qu'il est le plus à droite ou dans une autre position; et "décimal" car il utilise dix signes différents, y compris le zéro, pour représenter les nombres de zéro à neuf (ce qu'on appelle les "chiffres").
Puis, pour noter un nombre quelconque fait de n unités, il "regroupe" les unités en paquets de dix, et représente par exemple douze par 12, qui veut dire "un paquet de dix unités et encore deux unités". Cent-vingt-huit est représenté par 128, car il contient dix paquets de dix unités (c'est-à-dire un paquet de cent unités) plus encore deux paquets de dix unités plus huit unités.
Le fait que le nom d'un nombre soit en général très proche de sa représentation décimale ne doit pas être source de confusion. Il faut bien se rappeler que les nombres viennent avant leur notation et leur nom, lesquels sont dans une certaine mesure arbitraire. Ainsi, par exemple "une grosse" est le nom d'un nombre précis. Savez-vous lequel ?
Encore un exemple : prenons deux-mille-cinq-cent-quarante-quatre. Pour le représenter on regarde combien de fois
- une grande puissance de dix tient dedans, mettons qu'on commence par dix-mille : ça tient zéro fois
- puis la puissance plus petite : mille tient deux fois, et il reste cinq-cent-quarante-quatre
- dans le reste, cent tient cinq fois,
- etc.
et on note ce nombre, 2 suivi d'un 5 suivi d'un 4 suivi d'un 4.
2544 veut simplement dire "le nombre qui est égal à deux fois mille plus cinq fois cent plus quatre fois dix plus quatre".
Il y a d'autres systèmes de notation des nombres, aussi malins que le système indo-arabe (c'est-à-dire plus malin que le système romain), mais qui utilisent une autre collection de chiffres élémentaires. Le plus connu est le système à base deux.
(On pourra aussi consulter la leçon apprendre à compter et reproduire les calculs à l'aide de billes dans la deuxième rangée du "boulier" à partir de la droite, qui ne valent plus dix "billes unité", mais quinze, ou sept, ou cinq, ou deux...)
Voyons comment fonctionne le système binaire. Eh bien, de la même manière que le système indo-arabe à base dix ! Mais maintenant, on va regarder dans un nombre donné combien de fois tient deuxn, puis deuxn-1, puis... puis deux, puis 1.
On n'utilisera plus le signe "2", seulement les signes "0" et "1". Dix = deuxtrois + deuxun + zéro. Donc on le notera 1010, car la position la plus à droite est le nombre de fois qu'on a deux0, celui juste à sa gauche est le nombre de fois qu'on a deux1, etc.
Les algorithmes d'addition et de multipliation sont les mêmes qu'en système à base dix (voir vidéo pour détails) :
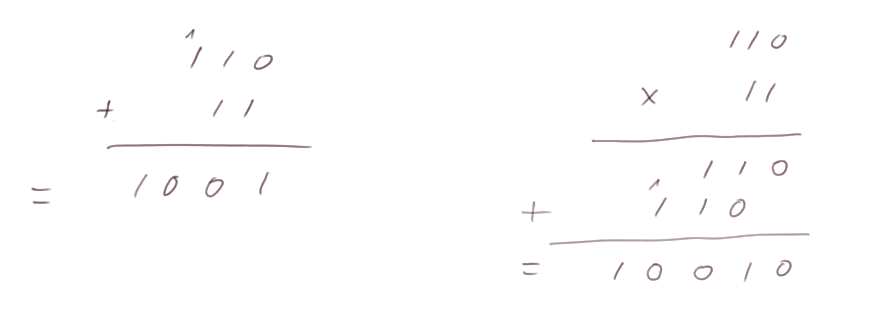
110 veut dire (1 x deux2 + 1 x deux). C'est donc six.
11 veut dire (1 x deux + 1). C'est donc trois.
six + trois égal neuf, qui est noté 1001.
trois fois six égal dix-huit, qui est noté 10010.
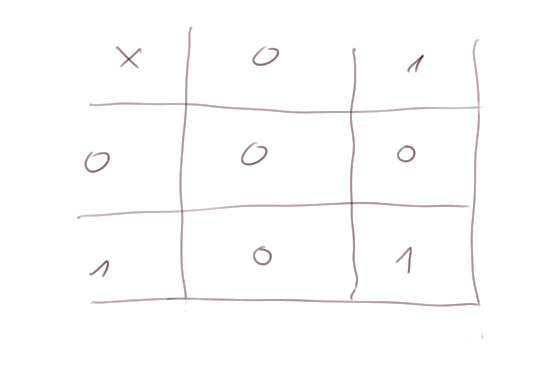
Apprendre sa table de multiplication est devenu très simple !
Question 1 : Peut-on "faire des fractions" en système à base deux ?
Réponse : Oui, tout à fait ! Les nombres et les fractions n'ont rien à voir avec leurs notations indo-arabes ou autres.
Quelle est la fraction trois-quarts ? Eh bien, comme d'habitude, on divise, sur la demi-droite de représentation des nombres, le segment [0, trois] en quatre parties égales. Le bord à droite du quart le plus à gauche est la fraction trois-quarts.
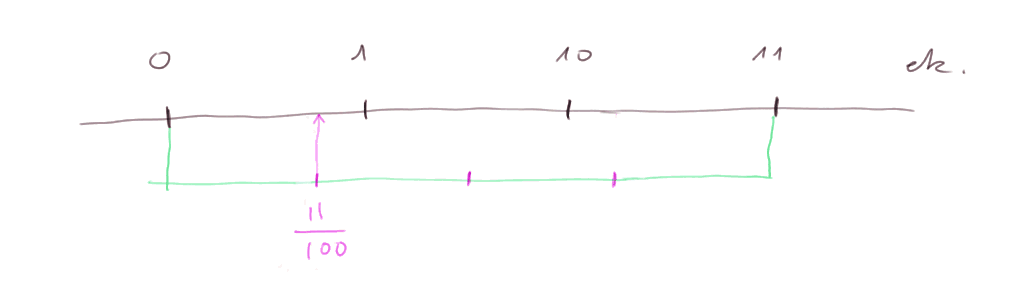
(dans le dessin ci-dessus, les nombres sont notés en système binaire)
Question 2 : Peut-on écrire des nombres avec virgule en système binaire ?
Réponse : Oui. De la même manière qu'en système décimal, les chiffres après la virgule comptent des dixièmes, des centièmes, des millièmes, etc. en système binaire, les chiffres après la virgule (qui ne peuvent être que 0 ou 1) comptent des demis, des quarts, des huitièmes, etc.
Ainsi le nombre, qui en système décimal se note 2,5 , en système binaire se note 10,1.
D'ailleurs comme pour 2,5 qui est 25/10, en système binaire 10,1 = 101/10 (c'est-à-dire "cinq" divisé par "deux").
Pour conclure : quand on pense au nombre "dix", il ne faut pas se focaliser sur la notation 10. Penser plutôt à dix petits cailloux :

Ces dix petits cailloux peuvent toujours se ranger en deux rangées de cinq (et ça n'a rien à voir avec leur notation décimale ou binaire) :

Ça montre que dix = deux fois cinq. En système à base dix, on le note 10 = 2 x 5. En système à base deux, on le note 1010 = 10 x 101.
Exercices
- En système à base deux, additionner 110011 par 101.
- En système à base deux, multiplier 110011 par 101.
- En système à base deux, à partir de la représentation d'un nombre N, comment obtient-on la représentation de son double?
Plan général du cours
Contacter le professeur
Réponses
- 111000, c'est-à-dire cinquante-six.
- 11111111, c'est-à-dire deux-cent-cinquante-cinq.
- On rajoute un zéro à droite.