Cours de mathématiques de 4e"Comment le résoudre ?"
|
|
|
|
|
Video |
|
Texte
George Polya (1887 - 1985) est un mathématicien d'origine hongroise qui enseigna d'abord en Europe, puis à partir de 1940 aux Etats-Unis.

Il a écrit, en 1945, un merveilleux petit livre intitulé "How to solve it?" pour aider les élèves en mathématiques.
Ses conseils s'organisent en 4 parties, et sont illustrés d'exemples. Les quatre parties sont :
- Comprenez le problème
- Faites un plan d'attaque du problème
- Mettez en œuvre votre plan
- Vérifiez votre solution
Comprenez le problème : ça a l'air idiot, mais trop souvent on se lance dans la recherche de la solution d'un problème, sans bien comprendre le problème lui-même d'abord. Il faut pouvoir exprimer le problème en bon français sous la forme la plus claire possible.
- Que faut-il trouver ?
- Y a-t-il une valeur inconnue ?
- Y a-t-il une contrainte sur la valeur inconnue ? (C'est ce qu'on a fréquemment rencontré avec nos équations.)
- Peut-on faire un dessin ?
- A-t-on suffisamment d'information pour résoudre le problème ? (Par exemple, si je vous dis que Cindy a deux ans de plus qu'Elodie, et je vous demande leurs âges, vous n'avez pas suffisamment d'information. Mais si je rajoute, et Cindy a une fois et demi l'âge d'Elodie, alors là vous avez assez d'information pour connaître l'âge de chacune d'entre elles. Réponse.)
Faites un plan d'attaque : voici quelques suggestions pour construire le plan d'attaque
- Tout d'abord, simplement : peut-on deviner la solution ?
- Cherchez une structure, une forme qui émerge. C'est ce qu'on a vu dans le développement décimal d'une fraction : si le développement décimal ne s'arrête pas, alors il y a une boucle dans le développement infini.
- Résolvez d'abord un problème plus simple. C'est une recommandation particulièrement importante dans la construction de logiciels informatiques : si on doit fabriquer un logiciel qui utilisera 42 objets similaires, commencez par une version qui n'en utilisera que 2.
- Partez de la solution et allez à l'envers vers les données initiales. Peut-être cela suggèrera-t-il le chemin de la démonstration.
- Raisonnez par l'absurde. C'est-à-dire supposez que ce qu'on veut démontrer soit faux, et montrez que ça conduit à une absurdité.
On peut trouver aussi de l'inspiration dans la liste de procédés heuristiques ci-dessous. Heuristique veut dire "recherche créative, intuitive, sans souci de grande rigueur logique".

source : Wikipedia, article sur "How to solve it?"
L'analogie est souvent une bonne approche. Y a-t-il un problème dans un autre domaine, qui a finalement la même forme ?
Généralisation : peut-on voir notre problème comme un cas particulier d'un problème plus général dont on connait la solution ?
Induction : peut-on logiquement étendre une solution d'un cas plus simple vers le cas qui nous concerne ?
Spécialisation : contraire de généralisation.
Décomposition du problème : travailler sur des parties du problème, et reconstituer le problème entier ensuite.
Travailler à l'envers : partir de la solution.
Mettez en œuvre votre plan : s'il ne marche pas, changez de plan.
Vérifiez votre résultat : c'est important non seulement pour éliminer les erreurs, mais aussi car ça conduit parfois à un éclairage nouveau du problème.
- Peut-on maintenant voir pourquoi c'est la solution ?
- Y a-t-il une méthode plus simple ?
Exemple 1 : soit un triangle quelconque ABC. Trouver, à l'aide seulement d'une règle graduée et d'une équerre, le carré de surface maximale, qui est le long de BC et qui tient entièrement dans le triangle.
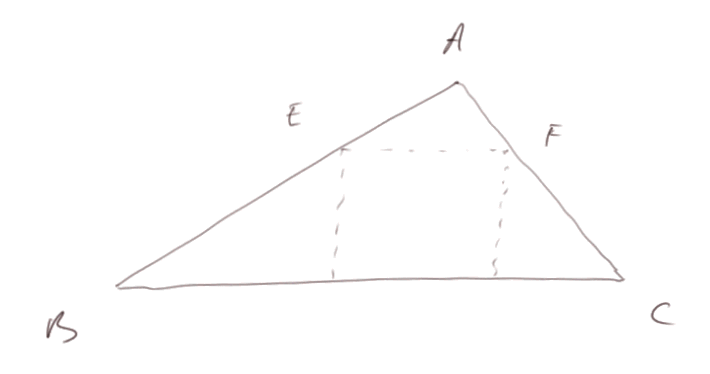
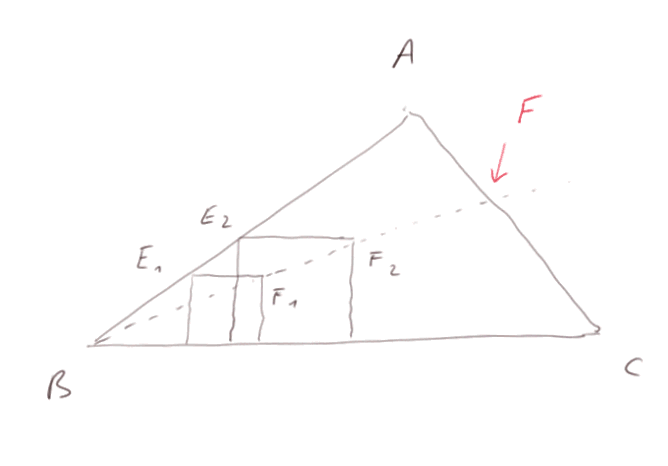
Polya suggère : "Essayez plusieurs carrés où E est sur AB, mais F est n'importe où dans le triangle." On voit tout de suite, par application du résultat général sur les proportionnalités dans des triangles de même forme (on le démontrera dans la leçon suivante), que les points F sont tous alignés avec B. Donc le point F solution du problème devient évident.
Exemple 2 : Montrer que la somme des inverses des nombres entiers jusqu'à n s'accroit indéfiniment quand n augmente.
Appelons Sn la somme jusqu'à 1/n. Donc on veut montrer que Sn augmente indéfiniment quand n augmente. On dit que Sn "tend vers l'infini".
Ici, une approche consiste à raisonner par l'absurde. Supposons que les Sn ne tendent pas vers l'infini. Alors forcément ils s'approchent d'un nombre L. On va montrer que c'est impossible.
Si Sn s'approche de plus en plus (par la gauche, sur la droite de représentation des nombres) de L, alors pour deux nombres n et m suffisamment grands (avec m > n), Sm - Sn devient aussi petit qu'on veut.
Intéressons-nous à S2n - Sn :
S2n - Sn = 1/(n+1) + 1/(n+2) + ... + 1/2n
Il y a n termes dans cette somme.
Chacun est supérieur ou égal au dernier (qui est 1/2n). Donc S2n - Sn est supérieur à n fois 1/2n = 1/2.
C'est une absurdité compte tenu de notre hypothèse.
Donc Sn ne peut pas tendre vers une limite L.
Sn diverge.
Exercices
- Dans l'exemple 1 : quellle est la surface du carré si le triangle est équilatéral ? (Rappel : la hauteur d'un triangle équilatéral est égale au côté multiplié par racine de trois sur deux, soit environ 86,6%)
- Quelle est la limite de la somme 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 etc. ?