Cours de mathématiques de 4eLe cosinus et la tangente d'un angle. Théorème d'Al-Kashi |
|
|
|
|
Video |
|
Texte
De même qu'on a défini le sinus d'un angle, on définit son cosinus et sa tangente :
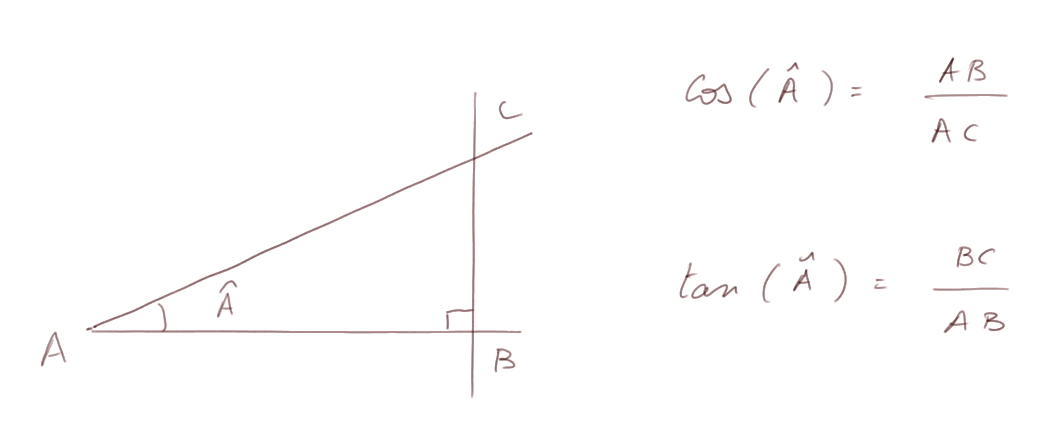
Naturellement ces trois mesures (sin, cos, et tan) associées à un angle ont des relations simples entre elles :
1) la tangente de l'angle A est le rapport du sinus au cosinus
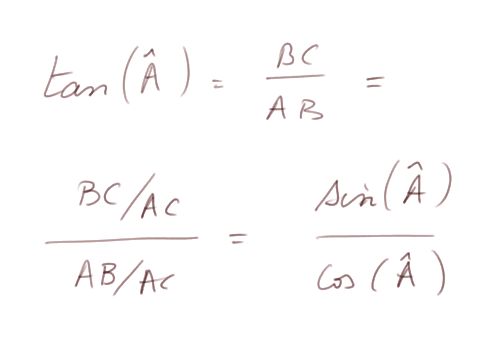
2) la relation la plus fondamentale est
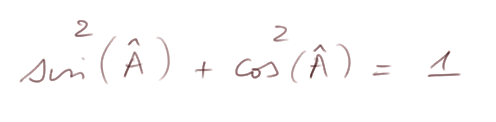
C'est une application immédiate du théorème de Pythagore.
Comme les angles A et C se complètent pour faire 90°, on voit aussi que cos(A) = sin(90 - A) et sin(A) = cos(90 - A).
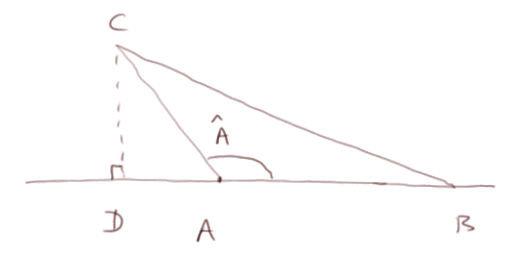
En classe de troisième nous continuerons l'étude des sinus et cosinus. En particulier nous les définirons dans notre repère habituel, où A sera l'origine et la droite AB sera l'axe des abscisses (= l'axe horizontal). Le cosinus de l'angle A, compris entre 90° et 180°, sera défini comme le rapport des longueurs AD/AC, avec le signe moins devant, car D est du côté des nombres négatifs sur l'axe horizontal.
Nous rencontrerons dans les années qui viennent de nombreuses propriétés merveilleuses des sinus, cosinus et tangentes. Pour l'instant limitons-nous à celle-ci :
Thèorème d'Al-Kashi : dans un triangle quelconque c2 = a2 + b2 - 2ab x cos(C)
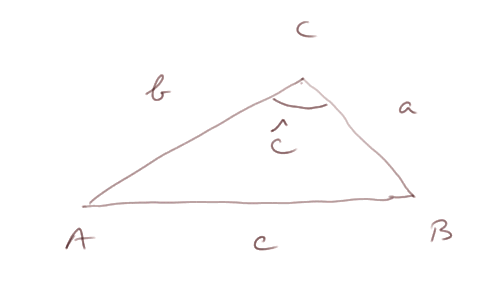
Démontrons ce résultat, dans le cas de figure où C est un peu plus grand que 90° (et donc cos(C) est un nombre négatif) :
on trace la hauteur issue de B vers le segment AC, qui l'atteint au point H. Et la longueur du segment HB est notée h.
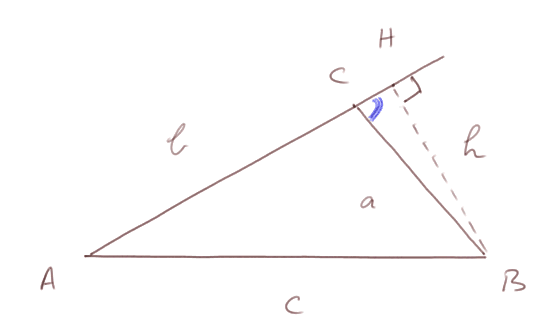
Par Pythagore appliqué dans le triangle AHB, on a c2 = h2 + AH2 = h2 + (b + CH)2
On développe le produit (b + CH)2 et on obtient c2 = h2 + b2 + 2 x b x CH + CH2 .
Notons que h2 + CH2 = a2, donc on arrive à
c2 = a2 + b2 + 2 x b x CH
Maintenant notons aussi que le rapport des deux longueurs CH/a = cosinus (angle bleu) = -cos(C) (puisqu'on va mesurer le cosinus de C avec un signe moins devant).
Finalement on aboutit à la formule à démontrer : c2 = a2 + b2 - 2ab x cos(C).
(Dans le cas de figure où l'angle C est plus petit ou égal à 90° la démonstration est encore plus simple.)
Le théorème d'Al-Kashi est une généralisation du théorème de Pythagore. (Al-Kashi était un Perse qui vécut entre 1380 et 1429.)
En effet, si l'angle C fait 90°, son cosinus est égal à zéro, et on retombre sur le théorème de Pythagore.
Exercices :
- Vérifier sur une feuille de papier, avec une règle graduée et un compas, le théorème de Al-Kashi quand C fait 120° (utiliser cos(120°) = -1/2), et les angles A et B sont de votre choix.