Cours de mathématiques de 4e Développer un produit
Video

Texte

Parmi les opérations les plus simples du calcul littéral, il y a :

1. développer un produit : (a + b)c → ac + bc,
   
   
2. et l'opération inverse, factoriser une expression :
   ac + bc → (a + b)c

De même (a + b)(c + d) = a(c +d) + b(c + d) = ac + ad + bc + bd

Souvent une des lettres représentera un nombre qu'on veut trouver. En général on le note x (c'est l'une des raisons pour lesquels on abandonne peu à peu ce signe pour signifier "multiplier"). Par exemple :
x + a = b. Trouver x.
Alors x = b - a.

Exemple : trouver x tel que x + 3 = 2. Eh bien x = 2 - 3 = -1.

Souvent encore la valeur x à trouver apparaîtra dans des formules contenant des produits comme (x + a)(x + b)(x + c). "Développons" ce produit en utilisant de manière répétée la distributivité de la multiplication sur l'addition :
-> x(x + b)(x + c) + a(x + b)(x + c)
-> x(x² + bx + cx + bc) + a(x² + bx + cx + bc)
-> x³ + bx² + cx² + bcx + ax² + abx + acx + abc

Généralement on aime bien réorganiser les termes pour mettre ensemble tout ceux avec x³ (il n'y en a qu'un), tous ceux avec x², tous ceux avec x, et tout ceux sans aucune puissance de x.
-> x³ + ax² + bx² + cx²+ abx + acx + bcx + abc

ax², bx² et cx² s'appellent "les termes en x²", et abx, acx et bcx s'appellent "les termes en x".

Parfois on refactorise partiellement pour souligner cette forme :
-> x³ + (a+ b+ c)x²+ (ab + ac + bc)x + abc

Exemple : (x + 2)(x + 1)(x + 5) = x³ + (2 + 1 + 5)x²+ (2 + 10 +5)x + 10 = x³ + 8x²+ 17x + 10

Développements particuliers :

(x + 1)² = x² + 2x + 1

(x + 1)³ = x³ + 3x² + 3x + 1

(x + 1)⁴ = x⁴ + 4x³ + 6x² + 4x + 1

D'une manière générale, dans le développement de (x + 1)ⁿ, les coefficients des puissances de x sont les nombres qui apparaissent dans le triangle de Pascal (voir video pour explication) :

 

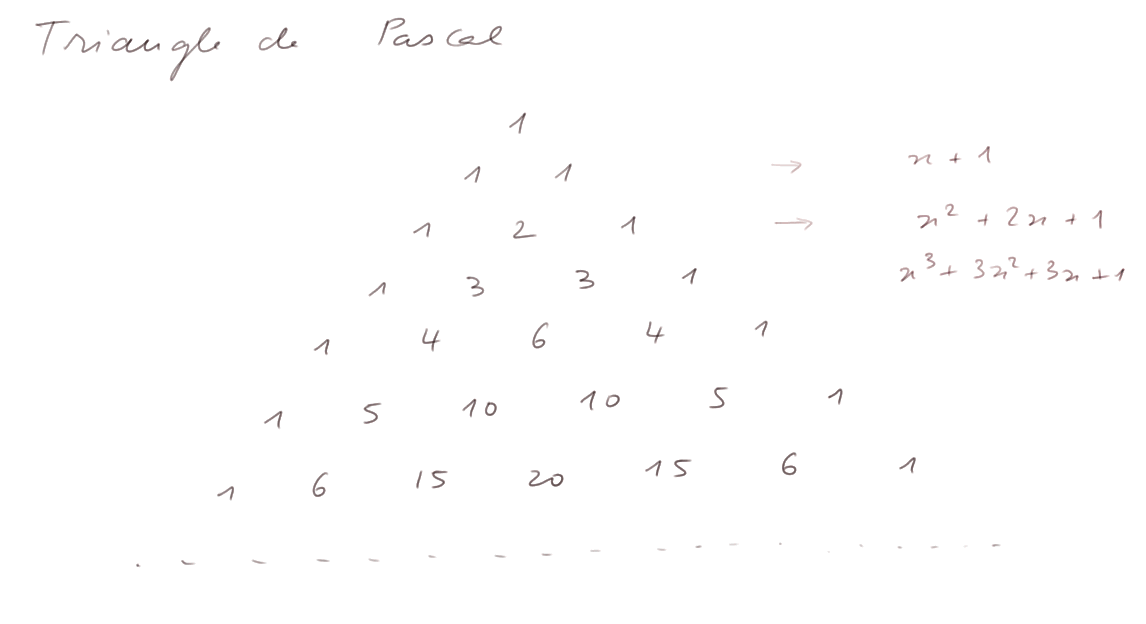
Exercices

1. Développer (x + 3)(x - 2)

Réponses

 

Un peu de maths plus avancées

Le triangle de Pascal apparaît dans de nombreuses situations mathématiques, en particulier en probabilités. Il faut savoir que Blaise Pascal (1623 - 1662) a fait beaucoup progresser la compréhension des probabilités au XVIIe siècle.

Ainsi, considérez une planche en bois dans laquelle on a planté des clous en quiconce comme ci-dessous. Les clous sont les points en grisé.

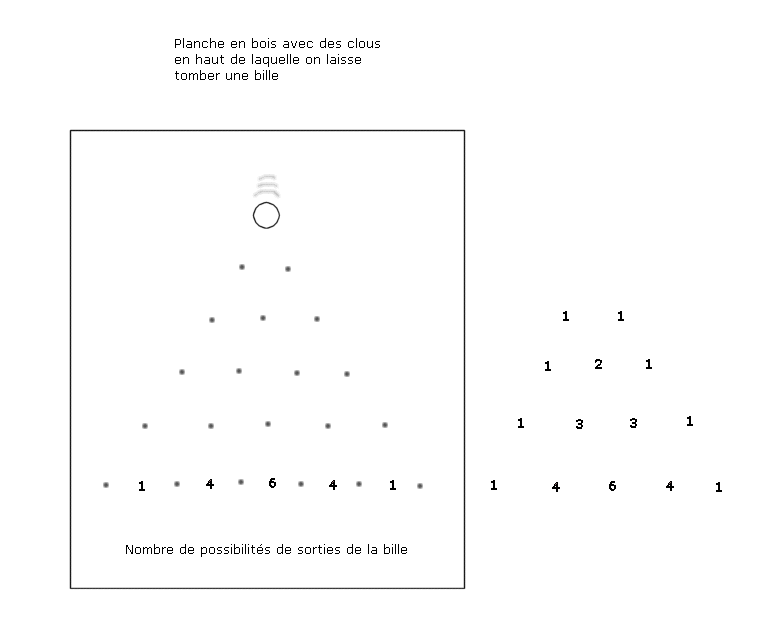
On lâche une bille en haut du quiconce de clous. Elle passe la première "porte", puis chaque fois qu'elle heurte un clou, elle peut aller soit à droite soit à gauche.

A la deuxième rangée de clous, le nombre de chemins pour aller entre les deux clous à gauche est 1, et entre les deux clous à droite est 1 aussi. C'est aussi les deux nombres de la rangée n°2 du triangle de Pascal.

A la troisième rangée, il y a trois intervalles de clous. Les chemins possibles pour y arriver sont au nombre de 1, 2 et 1.

Nous avons représenté la planchette avec cinq rangées de clous. A la cinquième rangée, le nombre de possibilités d'arriver dans chaque "porte" est 1, 4, 6, 4 et 1.

Ainsi le triangle de Pascal représente aussi des nombres de chemins possibles pour arriver à une "porte" d'une rangée donnée.

Pour finir, si on continue avec un plus grand nombre de rangées, et qu'on représente les nombres de la rangée n par des barres verticales les unes à côté des autres de hauteur proportionnelle aux nombres, on obtient un dessin qui s'approche de la forme d'une cloche.

Cette cloche a été beaucoup étudiée par le grand mathématicien Carl Friedrich Gauss (1777 - 1855). Elle joue un rôle fondamental dans de nombreuses situations mathématiques et physiques.

 

Plan général du cours

Contacter le professeur

 

 

Réponses : x² + x - 6