Cours de mathématiques de 4e Une équation : contrainte sur un nombre inconnu à trouver
Video

Texte

Nous arrivons maintenant aux équations, qui sont un des concepts centraux en mathématiques.

Une équation, c'est le résultat de la transformation d'un problème, où il faut trouver un nombre inconnu, en une expression, en partie littérale et en partie numérique, sur laquelle il y a une contrainte.

Les quatre concepts clé sont :

1. le problème (d'origine pratique, agricole, industrielle, économique, physique etc. ou déjà mathématique)
2. le nombre inconnu à trouver
3. la mise sous forme d'une expression mélangeant l'inconnue et des nombres
4. la contrainte

Voyons ce que ça veut dire.

On a déjà rencontré, en classe de 6e, des problèmes, c'est-à-dire en définitive des devinettes, que l'on a transformés en une expression littérale avec une contrainte. C'était le cas du problème : "Aujourd'hui Pépé a 63 ans et son petit-fils Jim a 3 ans. Dans combien de temps Pépé aura 4 fois l'âge de Jim ?".

On l'a transformé en : "Trouver n tel que 4(n + 3) = n + 63" (ou si l'on préfère 4(n + 3)/(n + 63) = 1, c'est-à-dire une expression littérale soumise à une contrainte, le terme de gauche devant être égal à 1). En effet dans le nombre d'années "n" à trouver, on veut avoir la relation 4(n + 3) = n + 63.

(n + 3 sera l'âge de Jim et n + 63 sera l'âge de Pépé.)

4(n + 3) = n + 63 est la contrainte sur n. On l'a transformée successivement en

• 4n +12 = n +63
• 4n = n + 51
• 3n = 51

Et on a trouvé évidemment que n doit être égal à 17.

Ici on a appelé la variable inconnue "n", on aurait pu l'appeler "x". (J'avais construit le problème de telle sorte que la solution soit un nombre entier, car on l'a étudié avant les fractions...)

On a "résolu l'équation" avec un ensemble de techniques qui s'appellent "l'algèbre", c'est-à-dire une série de modifications et remplacements dans l'expression littérale soumise à une contrainte. Algèbre est la francisation du mot arabe "Al-jabr". Il apparaît dans le titre du célèbre livre "Kitab Al-jabr" (kitab = livre ; al-jabr = remplacement, complétion) écrit par Al Khawarizmi au début du 9e siècle, entre 800 et 850, qui exposait pour la première fois ces techniques de résolution de problème.

Une équation du type ci-dessus s’appelle une équation du premier degré, car l’inconnue x (ou n) apparaît dedans avec seulement sa puissance 1.

Il faut convenir que c’est relativement élémentaire à résoudre, une fois qu’on a bien compris pourquoi le problème a été transformé en cette équation. On apprend ça aux alentours de 12 ans.

 

 

Les mathématiciens du haut Moyen Âge et même de l’Antiquité avaient aussi rencontré des problèmes qui, une fois transformés en une équation, contenaient l’inconnue à une puissance supérieure à 1, en général 2.

Parfois ça revenait quand même à une équation du premier degré. D'autres fois non. Dans certains cas où ce n'était pas équivalent à une équation du premier degré, néanmoins on arrivait encore à trouver assez facilement la solution. Dans d'autres cas c’était plus compliqué. Il fallait alors mettre en œuvre des techniques algébriques un peu plus élaborées, qui ont occupé les mathématiciens du Moyen Âge pendant quelques siècles, car des phénomènes étranges pouvaient apparaître : deux solutions, une solution, pas de solution, ou des solutions bizarres sans interprétation géométrique naturelle.

Il faut se rappeler qu'un des grands problèmes de la Science c'est : "Est-ce que la Nature vient d'abord et on la décrit à l'aide des mathématiques ensuite, ou bien les mathématiques viennent d'abord et on les utilisent pour percevoir la Nature ?" En d'autres termes, y aurait-il beaucoup de choses qu'on ne percevrait pas car nous n'aurions pas les structures mentales pour seulement en être conscients.

On étudiera la solution des équations du second degré dans les années qui viennent.

Voici un exemple :

trouver la longueur x en mètre d’un rectangle, dont la largeur est (x – 2) et la surface est 5 mètres carrés

Aujourd’hui on transforme ce problème en : trouver x tel que x(x - 2) = 5.

Ce qui est équivalent à : trouver x tel que x² – 2x - 5 = 0

Avant d’écrire l'équation de ce problème sous la forme moderne (avec un terme en x², un terme en x, un nombre, et des signes + - x  ÷ et =) les mathématiciens de l’Antiquité et du Moyen Âge l’exprimait sous les formes les plus variées et poétiques. Mais ce n’était jamais que des questions de notations, les concepts, les idées étaient toujours les mêmes.

Pour les équations de ce type (ax² + bx + c = 0) les mathématiciens du Moyen Âge ont trouvé la forme générale de la solution. Cependant avant qu’on l’étudie nous-même, regardons comment une représentation graphique des différentes valeurs prises par x² – 2x - 5 quand x varie permet de trouver géométriquement la solution, de manière approximative mais précise.

On calcule d'abord la valeur de x² – 2x - 5 pour une série de valeurs de x entre 0 et 4.

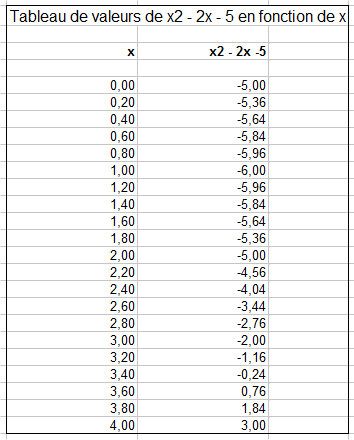
Maintenant on dessine ces couples de valeurs avec une représentation graphique dans notre repère habituel. Les différentes valeurs de x sont repérées sur l'axe horizontal, et à chaque valeur de x on met un point au-dessus, à la verticale, à la hauteur x² – 2x - 5 correspondante. (Le point est en dessous si la valeur x² – 2x - 5 correspondante est négative.)

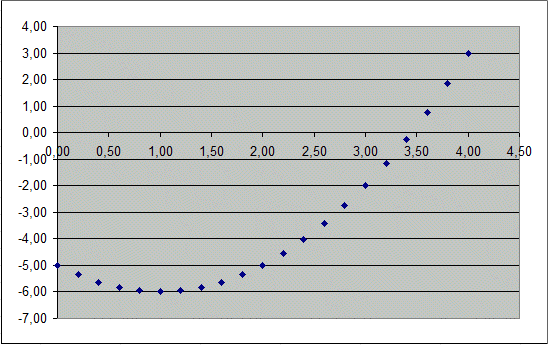
Avec ce graphe, on commence à bien voir pour quelle valeur de x, l'expression x² – 2x - 5 est égale à zéro ! C'est pour x vers 3,4 mètres.

On peut d'ailleurs vérifier, et même améliorer notre "solution géométrique" :

3,4 x (3,4 - 2) = 3,4 x 1,4 = 4,76 donc c'est un peu plus petit que 5. La solution doit être un peu plus grande que 3,4.

Essayons 3,5 :

3,5 x (3,5 - 2) = 3,5 x 1,5 = 5,25, c'est un peu trop fort.

Essayons la moyenne entre 3,4 et 3,5, c'est-à-dire 3,45 : on trouve 5,0025. Donc 3,45 mètres est une très bonne approximation de la solution exacte.

Nous apprendrons un peu plus tard à calculer, au moyen de manipulations algébriques, la solution exacte.

 

Exercice

1. Soit un rectangle de longueur x, de largeur 0,8x, et de surface 10m². Trouver sa longueur.
2. L'équation est-elle du premier ou du second degré ?
3. Soit un rectangle de longueur x, de largeur x + 3, et de surface 10m². Trouver x.

Réponses

 

 

Plan général du cours

Contacter le professeur

 

Réponses

1. Soit un rectangle de longueur x, de largeur 0,8x, et de surface 10m². Trouver sa longueur. Réponse : 3,54 mètres (approx.)
2. L'équation est-elle du premier ou du second degré ? Réponse : du second degré, mais c'est un cas où elle se ramène immédiatement à une équation du premier degré.
3. Soit un rectangle de longueur x, de largeur x + 3, et de surface 10m². Trouver x. Réponse : x = 2 mètres.