Cours de mathématiques de 4e

Le sinus d'un angle. Règle des sinus dans un triangle.

Texte

On a vu que les angles vont de 0° à 360°. En fait ils vont même plus loin car 370° est la même chose que 10°... Le sinus d'un angle est un nombre associé à l'angle. Commençons par les angles compris entre 0° et 90°.

Prenons un angle A comme sur la figure à gauche, et construisons un triangle rectangle comme sur celle de droite :

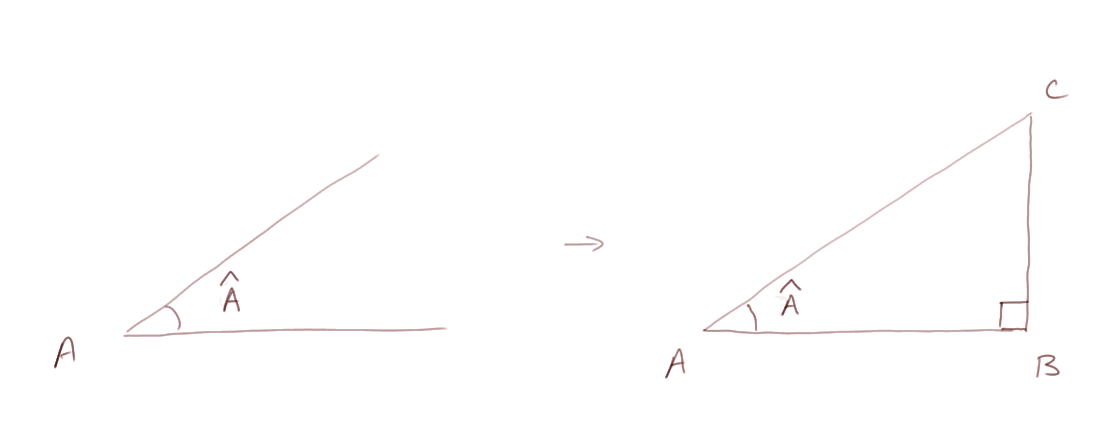
On appelle sin(A), lu "sinus de l'angle A", le rapport des longueurs BC/AC. C'est donc aussi le rapport du côté opposé à A sur l'hypoténuse.

Sinus de quelques angles particuliers :
sin(0°) = 0
sin(90°) = 1
sin(45°) = 1/(racine de 2)
sin(30°) = 1/2. Pour voir cela penser à un triangle équilatéral comme ci-dessous

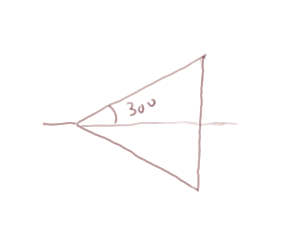
sin(60°) = (racine de 3)/2. Vérifions cela :

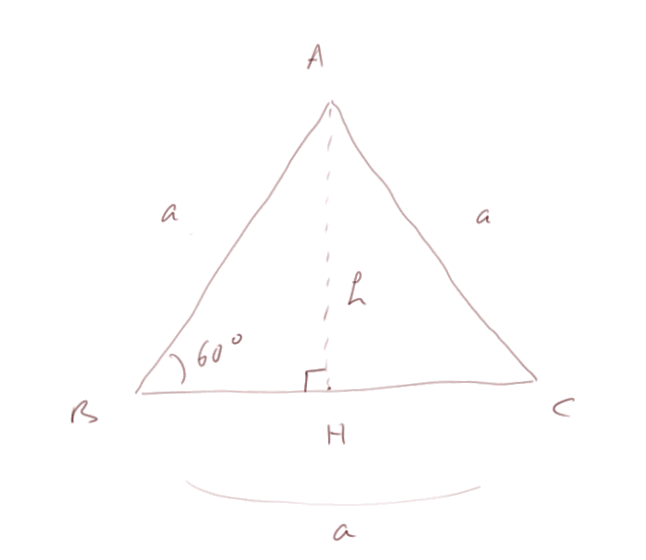
Appliquons le théorème de Pythagore dans le triangle ABH. On a h² + (a/2)² = a².

On divise de chaque côté par a², ça donne (h/a)² + 1/4 = 1. Donc (h/a)²= 3/4. Soit h/a = (racine de 3)/2. Et h/a est le sinus de l'angle B qui fait 60°.

Etendons la fonction sinus (c'est-à-dire la fonction qui à un angle quelconque fait correspondre son sinus) à des angles jusqu'à 180°.

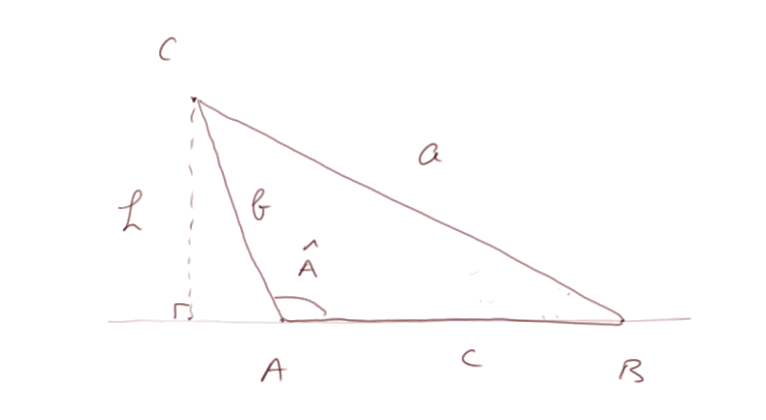
sinus de A est égal à h/b.

La règle des sinus : elle énonce une propriété remarquable des trois sinus d'un triangle quelconque.

Soit le triangle de sommets A, B et C. Notons avec un chapeau les trois angles correspondants, et a, b et c les longueurs des trois côtés opposés.

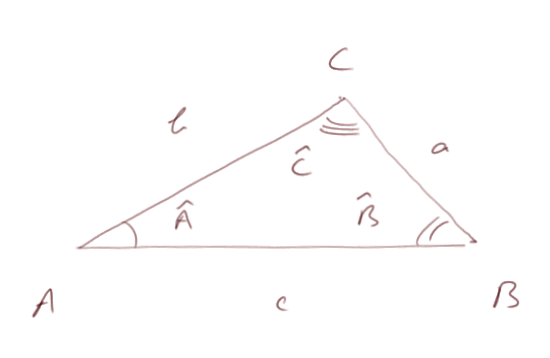
alors on a

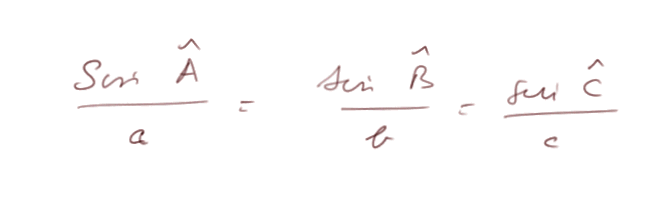
Montrons la première égalité dans le cas où les angles A et B sont plus petits que 90°.

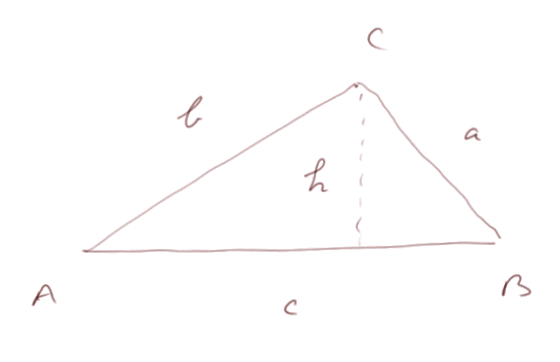
On a

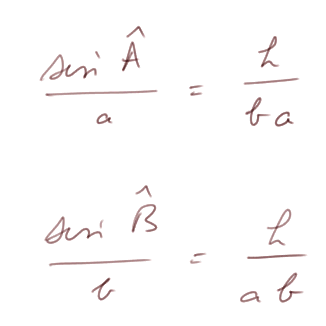
Donc les deux termes de gauche sont égaux. On le montre de la même manière pour l'angle C s'il est plus petit que 90° ; et on adapte un peu la démonstration si C est plus grand que 90°.

Cette propriété est très importante et utile en triangulation. La triangulation est la technique géométrique qui consiste à mesurer des distances (parfois de plusieurs kilomètres) à l'aide de mesures d'angles et de mesures d'autres distances. C'était très utile en cartographie avant les lasers et les satellites.

Supposons que dans le triangle ci-dessous, on connaisse l'angle A, l'angle B et la distance AB (= c). Alors on en déduit la distance CB (= a) de la manière suivante :

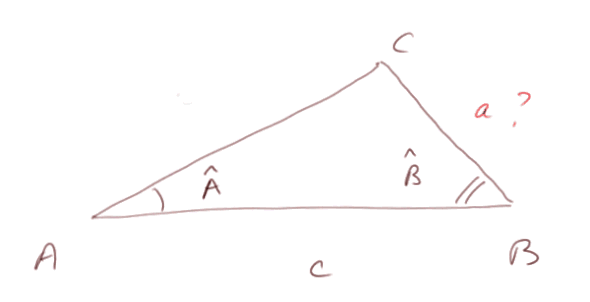
D'abord on déduit l'angle C (= 180° - angle A - angle B). Puis on a sin(A) / a = sin(C) / c. Donc

a = c x sin(A) / sin(C)

Autre propriété de sin(A) / a : c'est l'inverse du diamètre du cercle circonscrit au triangle.

Exercices

1. Démontrer que [ sin(A) / a ] est l'inverse du diamètre du cercle circonscrit au triangle.

Plan général du cours

Contacter le professeur