Cours de mathématiques de 5ePrismes droits et obliques |
|
Video |
Texte
Un prisme est un volume dans l'espace construit de la manière suivante :
- partir d'un polygone dans un plan (dans la figure ci-dessous c'est le triangle ABC)
- translater le polygone dans une direction sortant du plan
- fermer toutes les faces

La direction de la translation s'appelle la direction génératrice. Si elle est perpendiculaire au polygone initial, on parle de prisme droit. C'était le cas du prisme précédent :
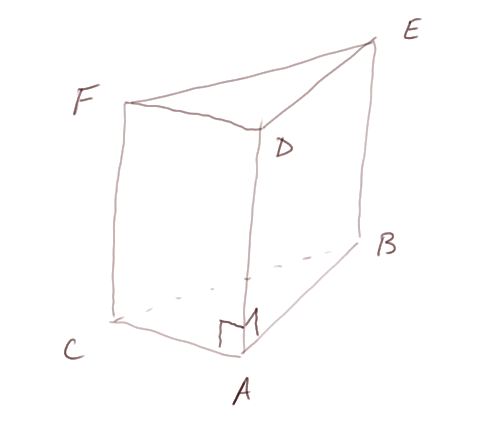
Quand la génératrice n'est pas perpendiculaire au plan de base, on parle de prisme oblique (ou de prisme quelconque).
Définition un peu plus "mathématique" : un prisme est un polyèdre formé de deux bases polygonales superposables, situées dans des plans parallèles, et dont les autres faces sont des parallélogrammes.
(Imposer que les autres faces soient des parallélogrammes empêche que le prisme soit "tordu" dans l'espace.)
Exemple simple : un parallélépipède rectangle est un prisme droit à base rectangulaire.
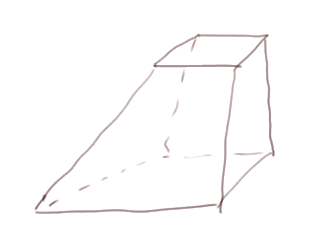
La figure ci-dessous n'est pas un prisme :
Volume d'un prisme : 1) cas d'un parallélépipède rectangle
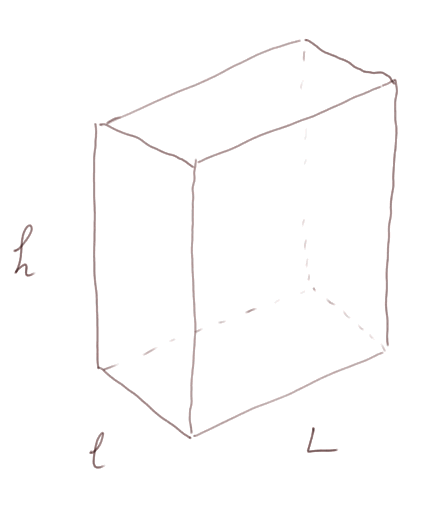
Nous avons déjà étudié ce cas en classe de sixième au début de l'étude des volumes. Pour un parallélépipède rectangle (= "une boîte de lait") c'est simplement : V = L x l x h
Volume d'un prisme : 2) cas d'un prisme droit à base un triangle rectangle
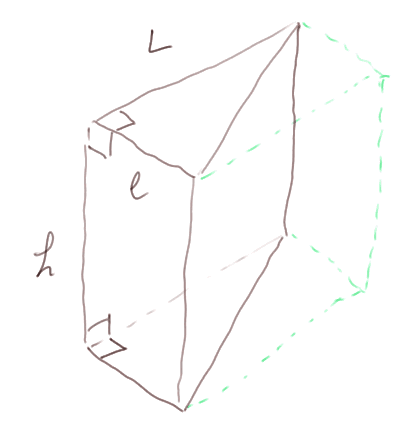
Ici le prisme est la moitié d'un parallélépipède rectangle, donc V = L x l x h / 2. C'est-à-dire V = surface de la base x hauteur.
Volume d'un prisme : 3) cas d'un prisme droit à base un triangulaire quelconque
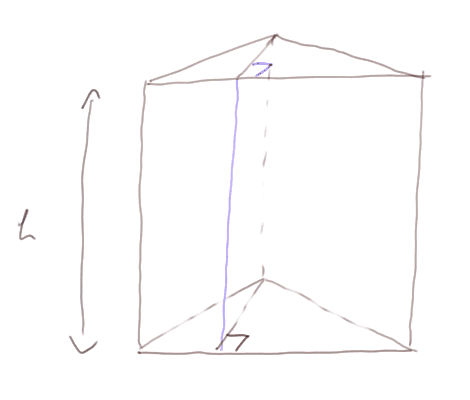
Comme on peut découper le prisme en deux prismes à base un triangle rectangle, on est ramené au cas précédent : V = surface de la base x hauteur
On note plus simplement V = S x h
Volume d'un prisme : 4) cas d'un prisme droit quelconque
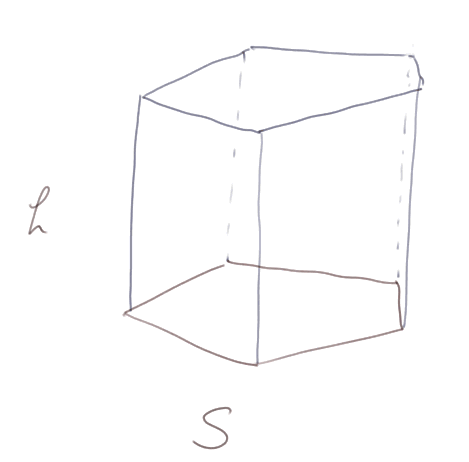
On peut découper le polygone de base en triangles et chacun d'entre eux en deux triangles rectangles, donc on est encore ramené au cas précédent :
V = S x h
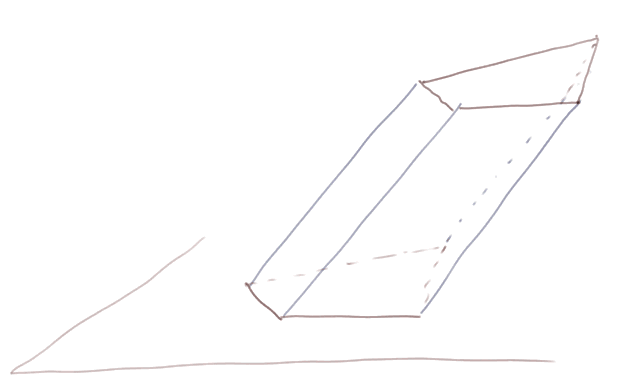
Volume d'un prisme : 5) cas d'un prisme quelconque (prisme rouge ci-dessous).
Ici, pour montrer que la formule est toujours la même, on va faire une opération audacieuse : on découpe le prisme rouge en fines tranches horizontales (tranches vertes) et on les fait glisser les unes sur les autres pour les empiler bien verticalement. On ne modifie pas les volumes en faisant ça. On arrive à un prisme droit avec les murs pas tout à fait lisses, mais comme on peut faire cette opération avec des tranches aussi fines qu'on veut, on peut s'approcher d'aussi près qu'on veut du vrai prisme droit de même base et même hauteur. Le volume du prisme droit est le produit de la surface de la base par la hauteur. C'est donc forcément vrai aussi pour le prisme oblique.
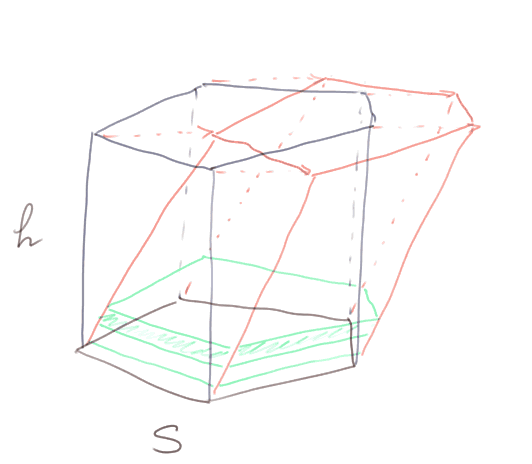
La formule V = S x h est encore vraie pour le prisme oblique.
Attention : dans le prisme oblique ci-dessus, h n'est pas la longueur d'une arête rouge inclinée, mais reste bien la hauteur du prisme, c'est-à-dire la distance entre les deux plans horizontaux qui ferment le prisme. La hauteur du prisme oblique est la même que celle du prisme droit.
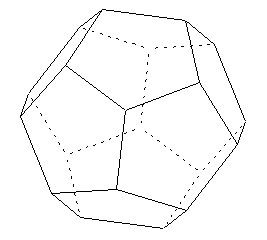
Les prismes sont un type particulier de polyèdres, c'est-à-dire de volumes dans l'espace délimités par des faces planes, et qui ont donc aussi des arêtes et des sommets. Voici un autre polyèdre (celui-ci est dit "régulier" car toutes les faces sont des polygones de la même forme) :
Nous étudierons dans la leçon suivante les pyramides. Exemples de pyramides :
Il existe une jolie formule générale, valable pour n'importe quel polyèdre (convexe, c'est-à-dire si deux points sont dans le polyèdre, tout le segment entre les deux points est aussi dedans), reliant le nombre de faces f, le nombre d'arêtes a, et le nombre de sommets s. On a toujours f + s = a + 2. Elle porte le nom de formule d'Euler pour les polyèdres, d'après le mathématicien suisse Leonhard Euler (1707 - 1783).
Vérifions-la pour les prismes à base triangulaire :

Ici f = 5, s = 6 et a = 9. On a donc bien f + s = a + 2.
Exercices :
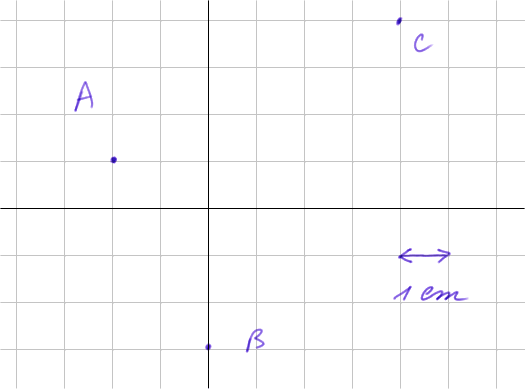
- Quel est le volume d'un prisme droit dont la base est le triangle avec les points suivants dans un repère sur le plan d'en bas, et la hauteur est 10 cm ? (Dessiner le triangle et utiliser une règle graduée pour mesurer les côtés.)
- Vérifier la formule d'Euler pour un prisme à base pentagonale (i.e. un polygone à cinq côtés)
Plan général du cours
Contacter le professeur
Réponses :
- Observer que le triangle est rectangle, AB fait 4,47 cm, et AC fait 6,71 cm. Donc le triangle a pour surface 15 cm2. Et le prisme a pour volume 150 cm3.
- f = 7, s = 10 et a = 15.