Cours de mathématiques de 5eRésoudre un problème : 2e exemple |
|
Video |
Texte
Dans la vie courante, on est souvent amené à choisir une solution parmi une collection, en prenant celle qui optimise quelque chose, c'est-à-dire qui est la meilleure selon un certain critère. Les ingénieurs rencontrent ce genre de problèmes quand ils construisent des ponts ou des moteurs. Nous allons "maximiser" une surface (= aire) à périmètre constant.
Avec un gros rouleau de grillage de 100 mètres de long nous voulons enclore un rectangle de longueur L et de largeur l. Quel est le rectangle, de périmètre 100 m, qui a la surface maximale ?
Nous allons résoudre le problème en essayant une série de longueurs L. Chaque fois, il faudra que 2L + 2l = 100m. Et pour chaque L on calculera S. Pour chaque L, la surface correspondante sera notée S(L).
Il est clair que L ne peut pas être plus que 50 m. Mais bien sûr ce ne sera pas la solution car alors l = 0, et S(50) = 0.
Faisons une série de calculs de 10 m en 10 m.

A l'aide d'un ordinateur et d'un tableur, on peut même faire des calculs plus complets. Voici les résultats de 5 m en 5 m :
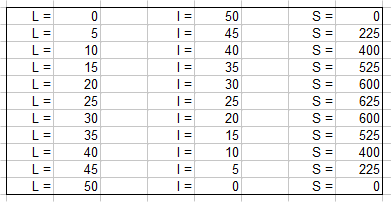
Bon, on voit déjà où est la longueur qui correspond à la surface maximale, mais commençons par représenter les surfaces en fonction de L, sur un graphique.
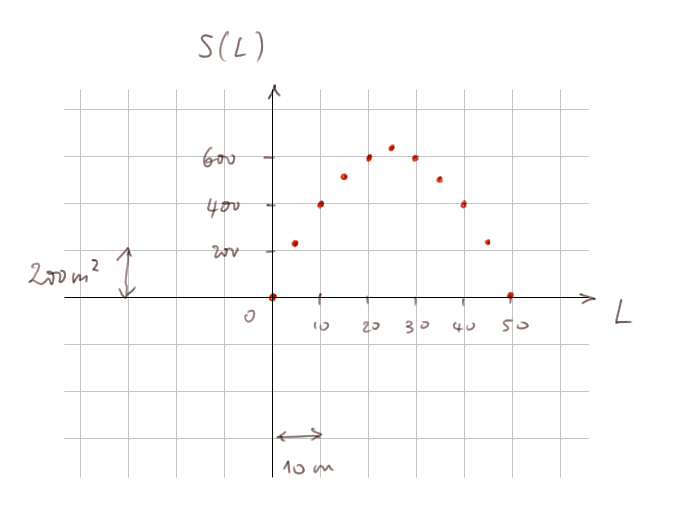
J'ai utilisé notre bon vieux repère. Sur l'axe horizontal, j'ai choisi qu'un petit segment corresponde à 10 m, et sur l'axe vertical un petit segment corresponde à 200 m2. Pour chaque longueur L, on se place sur sa position sur l'axe horizontal (appelé aussi "l'axe des abscisses") et on reporte un point au dessus à la verticale à la hauteur correspondant à S(L). On obtient la collection de points rouges ci-dessus. Si on prenait encore beaucoup plus de longueurs L, on obtiendrait une courbe.
On voit que la collection des points a un axe de symétrie vertical passant par la marque correspondant à L = 25 m sur l'axe des abscisses. La surface maximale est atteinte avec cette longueur-là, et est S(25) = 625 m2.
En d'autres termes, à périmètre donné (ici 100 m) le rectangle qui maximise la surface est un carré. Dans notre exemple il a pour côté 25 m.
Maintenant, regardons ce que donnerait un hexagone régulier de périmètre 100 m.
Un hexagone est un polygone à six côtés ("hexa" = 6, "gone" = côté). Un hexagone régulier est en fait un assemblage de 6 triangles équilatéraux.
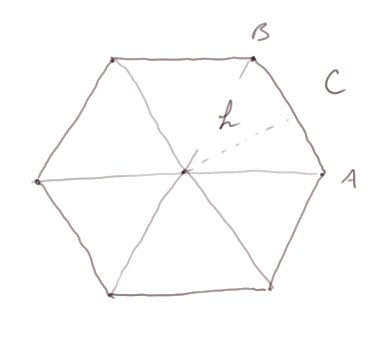
Soit C le côté de chaque triangle équilatéral dont la collection de six emboîtés forme l'hexagone. On a donc 6 x C = 100 m.
Par ailleurs, si vous dessinez très soigneusement avec une règle et un rapporteur ou un compas un triangle équilatéral, et mesurez une hauteur, vous verrez que h est approximativement égal à 86,6% x C. C'est vrai pour tous les triangles équilatéraux, car ils sont tous de la même forme : ce rapport ne change pas.
Surface de l'hexagone : S = 6 x C x h / 2 = 3 x C x 86,6% x C et C = 100 / 6.
Donc C = 16,67 m (approximativement), et S = 3 x 16,67 x 86,6% x 16,67 = 721,4 m2. (Maintenant qu'on connaît bien les calculs et comprend ce qu'ils signifient on peut utiliser notre calculette.)
On voit que c'est encore plus grand que 625 m2 !
En fait la surface maximale à périmètre constant est atteinte avec le cercle.
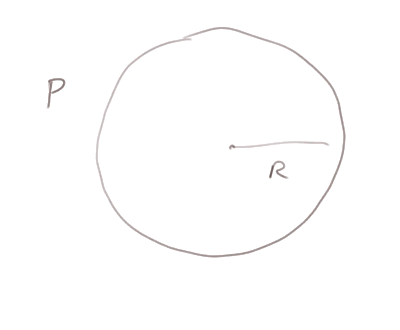
Soit P le périmètre (= 100 m). On a P = 2πR donc R = 100 / 6,28 (approx.) = 15,92 m.
Et S = πR2 = 796,6 m2. On ne peut pas faire plus grand.
Exercice :
- Des cultivateurs égyptiens au troisième millénaire avant J.-C. qui avaient les champs suivants (un côté de carreau fait 10 mètres)
les ont vu être effacés par la crue annuelle du Nil (qui apportait aussi de l'engrais). Maintenant le Nil s'est retiré, et ils décident de simplifier la forme de leurs champs, en trois rectangles tous avec un côté de 50 mètres. Quelles doivent être les longueurs des autres côtés des champs A, B et C redessinés ? (Aide : le segment noir au milieu du champ B, avant la crue, avait pour longueur 24 mètres.)