Cours de mathématiques de 6e5. L'addition |
|
|
|
|
Video |
L’addition ne présente pas de difficulté particulière. Si j’ai une collection de n objets, par exemple n = 75, et une autre collection de m objets, par exemple m = 27, et que je rassemble les deux collections d’objet en une seule, combien ai-je d’objets dans l'ensemble qu'elles forment ?
On peut le calculer de tête, on peut aussi le résoudre avec une calculette (surtout quand les nombres sont plus grands, ou qu’il y en a plus que deux). Mais il est important de bien comprendre comment s’effectue une addition. Les chiffres arabes, une fois de plus, opèrent des merveilles, alors qu’avec les chiffres romains c’est plus compliqué. Comprendre comment on effectue une grosse addition est utile pour comprendre les maths.
Pour commencer, il faut connaître sa « table d’addition ».
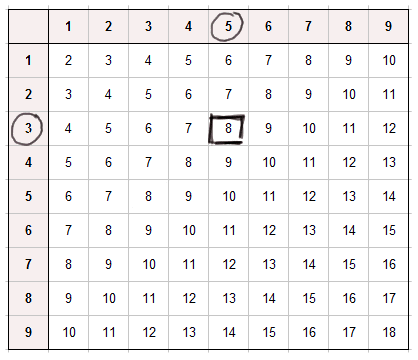
table d'addition
Dans l'exemple ci-dessus, on voit que 3 plus 5 égale 8.
Cette table a une structure simple. En particulier elle est symétrique par rapport à la diagonale qui va d'en haut à gauche à en bas à droite. Cela veut simplement dire que 3 + 5 donne la même chose que 5 + 3. Il faut néanmoins la connaître sans hésitation : 7 + 8 = ?
Ensuite, pour effectuer une grosse addition, le système des chiffres arabes permet de procéder de manière plus ou moins mécanique.
Exemple 1 (visionner la vidéo) : 75 + 27 = 102
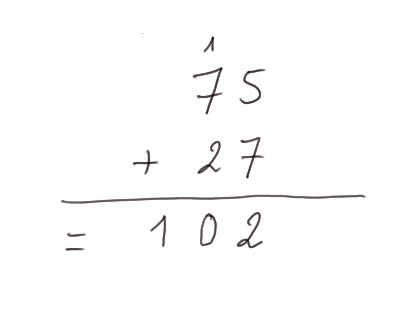
Deuxième exemple : 865 + 456 = 1321
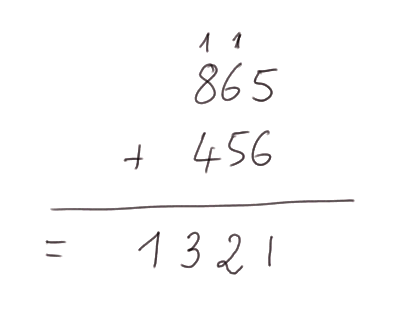
Troisième exemple : 865 + 456 + 28 + 183 = 1532
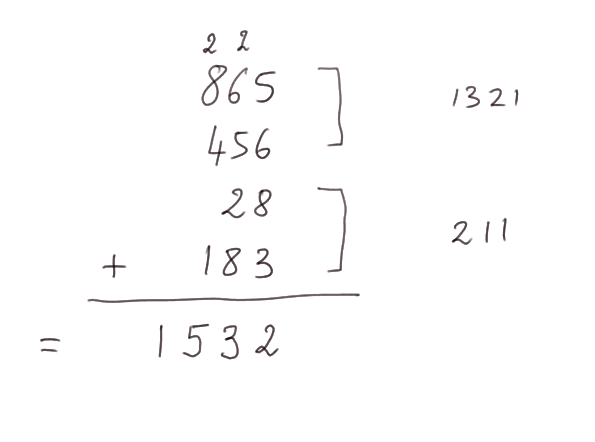
Autre façon de procéder dans le troisième exemple : on peut commencer par additionner des parties des quatre nombres.
Additionnons les deux derniers : 28 + 183 = 211
Par ailleurs on a vu que 865 + 456 = 1321
Enfin 1321 + 211 = 1532
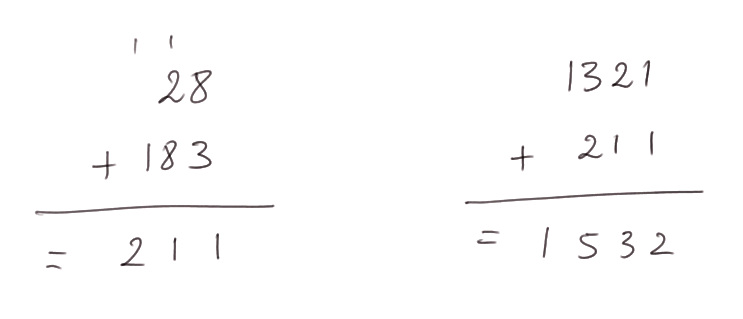
D’une manière générale, quand on a une collection de nombres à additionner, on peut faire des additions intermédiaires. On peut aussi changer l’ordre des nombres. Ça ne change rien au résultat.
Pour pratiquer les additions, faire celles présentées dans les pages suivantes :
Pour aller plus loin :
On a donc vu comment additionner deux nombres entiers. C'est une opération que chacun comprend intuitivement et qu'il est difficile d'expliquer plus qu'en en faisant un certain nombre.
À l'école primaire on a appris à bien maîtriser les notations avec les chiffres arabes (unités, dizaines, centaines, etc.) et à poser et effectuer les additions. On a appris à utiliser les retenues qui font partie des mécanismes à la fois simples et astucieux de la notation positionnelle à dix symboles.
Un point mérite d'être souligné : l'addition est une opération qui à deux nombres en fait correspondre un troisième.
Les mathématiques utilisent beaucoup les "opérations". L'addition est la plus simple d'entre elles. La deuxième plus simple est la multiplication. Elle est aussi intuitive que l'addition, et nous la verrons dans quelques leçons. Ensuite, en terme de caractère intuitif, viennent la soustraction et la division. Nous considérons la soustraction comme moins intuitive que la multiplication parce qu'on peut toujours multiplier deux nombres entre eux (c'est-à-dire additionner un certain nombre de fois le premier nombre, le "nombre de fois" étant le second nombre), alors qu'on ne peut pas soustraire à un nombre plus que lui-même.
Dans tous les cas, avec l'addition, à deux nombres on en fait correspondre un troisième. Ainsi cinq plus sept égale douze, ce que l'on note avec les chiffres arabes : 5 + 7 = 12.
Voir l'addition comme une "opération" (qui à deux nombres en fait correspondre un troisième) est une façon de voir importante, car le concept d'opération est très vaste et très riche, et quand on le voit bien on comprend mieux beaucoup d'autres activités mathématiques moins intuitives que l'addition de nombres entiers.