Cours de mathématiques de 6e29. Constructions symétriques |
|
|
|
|
Video |
|
Texte
Les figures géométriques habituelles que nous connaissons ont des propriétés de symétrie.
Un triangle isocèle quelconque a un axe de symétrie et pas de centre de symétrie.
Un triangle équilatéral a trois axes de symétrie. Il n'a pas de centre de symétrie. Rappelons-nous qu'une symétrie centrale est aussi une rotation de 180 °. Et aucune rotation de 180° ne laisse le triangle inchangé. En revanche, il se superpose à lui-même si on le fait tourner de 120° autour de son centre.
Un rectangle a deux axes de symétrie et un centre de symétrie.
Un parallélogramme quelconque n'a pas d'axe de symétrie mais a un centre de symétrie.
Un repère dans le plan permet de construire facilement des figures symétriques.
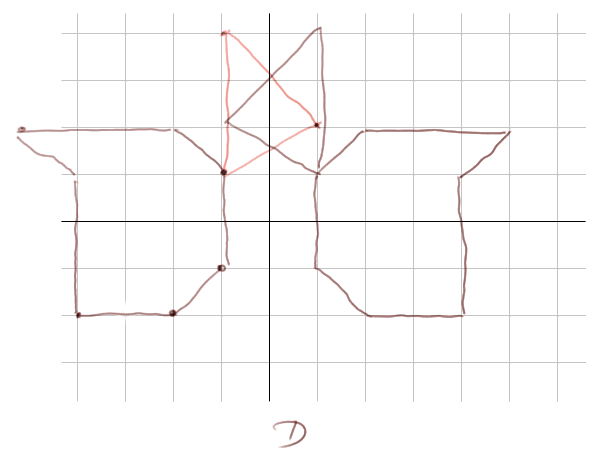
Symétrie axiale (c'est-à-dire par rapport à une droite) :
Symétrie centrale (c'est-à-dire par rapport à un centre, dite parfois symétrie radiale) :
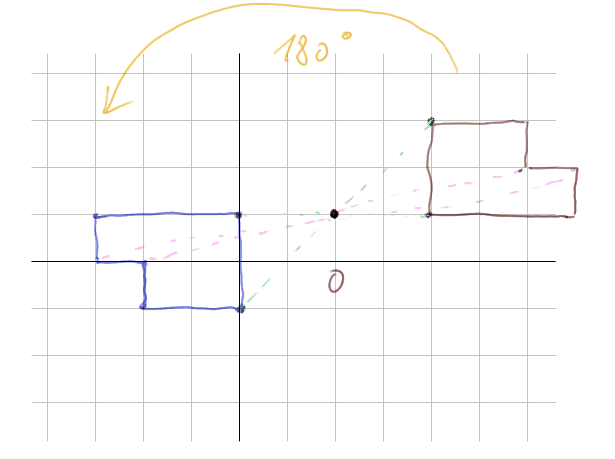
Une symétrie centrale est exactement la même chose qu'une rotation de 180° par rapport au centre de symétrie.
Dans une symétrie centrale une figure et sa transformée restent donc superposables. Tandis que dans une symétrie axiale (qui correspond à un retournement de la feuille, par pliage le long de l'axe de symétrie) une figure et sa transformée ne sont en général pas superposables.
Exercices
- Combien d'axes de symétrie a un cercle ?
Plan général du cours
Contacter le professeur
Réponses : une infinité. Tous les diamètres sont des axes de symétrie.