Cours de mathématiques de 6e31. Géométrie dans l'espace |
|
|
|
|
Video |
|
Texte
Nous allons étudier les formes, non plus dans le plan, mais dans l'espace : cubes, parallélépipèdes (par exemple, une maison avec quatre murs et un plancher et un toit horizontaux), sphères, plans dans l'espace (soit parallèles comme les étages d'un immeuble, soit qui se coupent comme deux murs d'une maison), surfaces non planes (comme un paysage vallonné, un tremplin de saut à ski, une selle de cheval).
Un premier problème se pose tout de suite : comment représenter nos formes et figures sur une feuille de papier ? On pourra aussi parfois utiliser du carton et de la colle pour construire nos formes, ou même du bois.
La perspective cavalière est le mode de représentation le plus courant d'une figure dans l'espace sur une feuille de papier (ou un écran d'ordinateur).
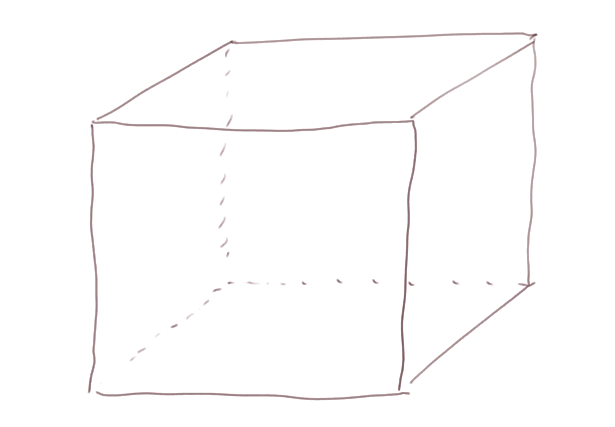
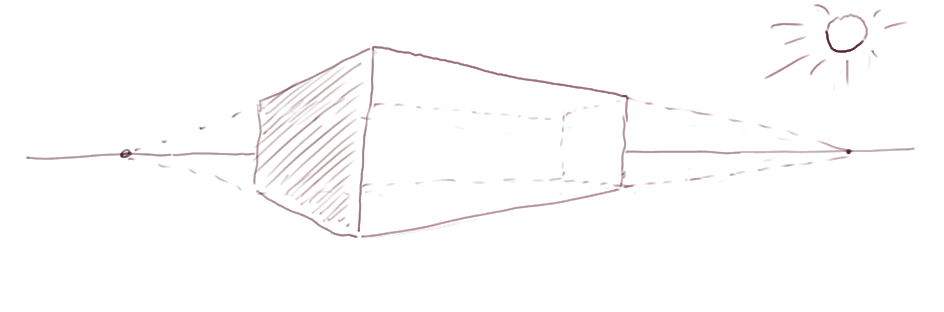
Les Italiens ont inventé au XVe siècle la perspective avec points de fuite. Alberti (1404 - 1472) a écrit un livre fondateur sur la perspective.
Nous représenterons les sphères (= un ballon de foot, la terre), les "sphères oblongues" (= un ballon de rugby), les plans qui se coupent,
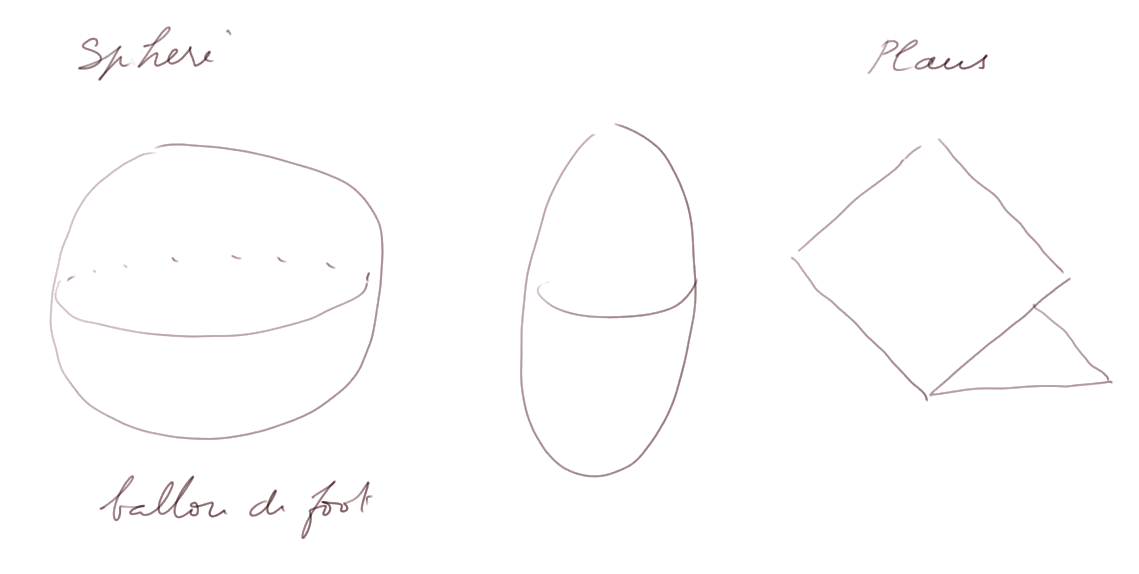
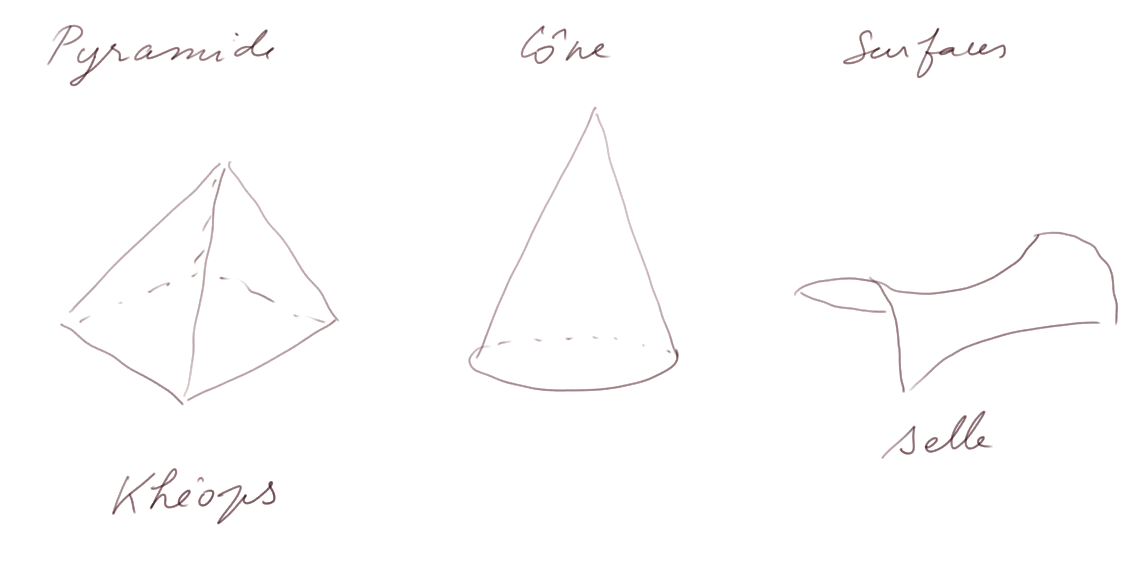
les pyramides (pensez à celle de Khéops, à côté du Caire en Egypte), les cônes (= cornets de glace, ou chapeaux de magicien), des surfaces non planes.
Tout ce petit monde se coupe et produit des courbes intéressantes. L'intersection de deux plans est toujours une ligne droite (penser à l'angle de deux murs ou à une arête de toiture).

l'intersection de deux plans est toujours une droite
L'intersection d'une sphère et d'un plan est toujours un cercle.
L'intersection d'un cône et d'un plan peut donner un cercle, une ellipse, une parabole, ou encore d'autres choses.
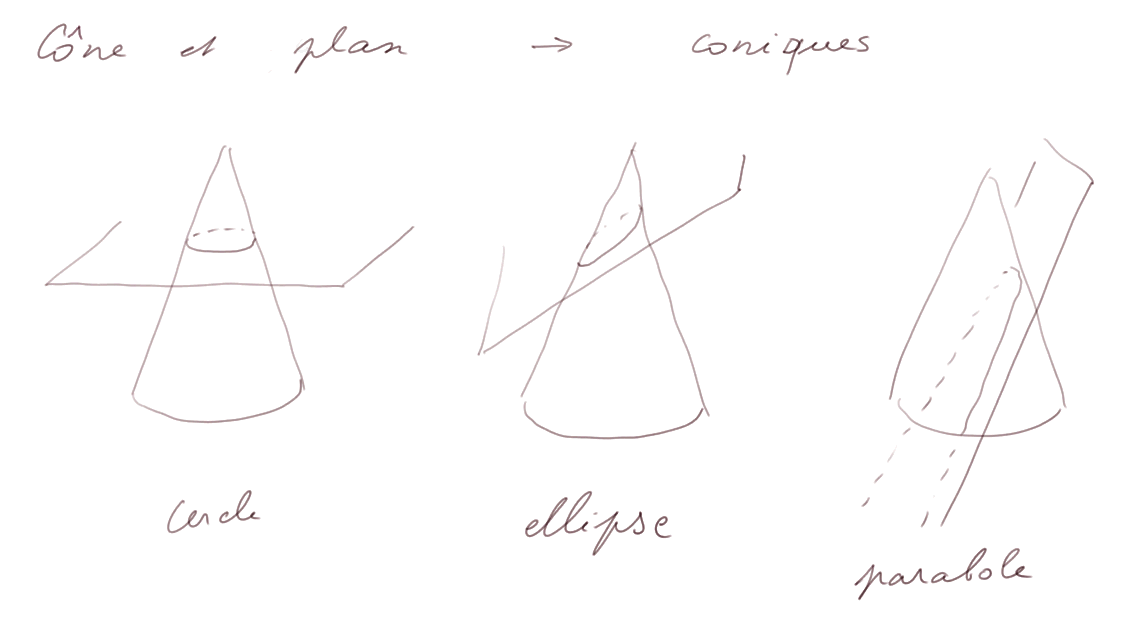
Ces courbes s'appellent les "coniques". On les étudiait beaucoup à l'école jusqu'au milieu du XXe siècle. Leur étude strictement géométrique est maintenant passée de mode. Elles servent en physique : un caillou jeté en l'air décrit une parabole ; les miroirs de téléscope sont taillés en paraboloïdes (en fait comme c'est difficile, on leur donne la forme de calotte sphérique qui est une approximation satisfaisante pour un paraboloïde assez plat).
Nous étudierons des transformations dans l'espace. On a déjà rencontré deux transformations dans le plan (symétrie axiale, et symétrie centrale). D'une manière générale, une "transformation" c'est une façon à chaque point d'un ensemble (plan, espace) de faire lui correspondre un autre point.
Dans l'espace, l'une des plus simples est la symétrie par rapport à un plan. (La plus simple de toute est la "translation" : à tout point de l'espace on fait correspondre un autre point par un déplacement, toujours de la même distance et dans la même direction.)
Les miroirs :
quand vous vous regardez dans un miroir, vous voyez en face de vous votre symétrique, comme si vous étiez aussi de l'autre côté du miroir. Mais dans le miroir, vous êtes "retourné" : si votre chemise a une poche à gauche, dans le miroir c'est une chemise avec poche à droite. Si vous vous coiffez avec une raie sur le côté, mettons à gauche, vous avez l'habitude dans le miroir de vous voir avec la raie à droite, cependant sur les photos vous portez la raie à gauche.
Les webcams :
quand on se "regarde avec une webcam", c'est-à-dire quand on se met devant un écran d'ordinateur en haut duquel est branchée une webcam, le logiciel qui affiche votre visage sur l'écran fait un choix : soit il vous montre comme quelqu'un d'autre vous voit, soit il vous montre comme vous vous voyez vous-même dans un miroir. Par exemple, le logiciel "paper camera" pour tablettes android fait le choix de vous montrer comme dans un miroir, puis, quand vous avez pris la photo, il la retourne pour l'afficher comme vous voit quelqu'un d'autre.
Une belle transformation dans l'espace est la projection à partir d'un point de tous les points d'un plan vers un autre plan. Pensez à une lampe qui éclaire une figure en fil de fer placée sur le plan incliné et qui projette son ombre sur le plan horizontal.
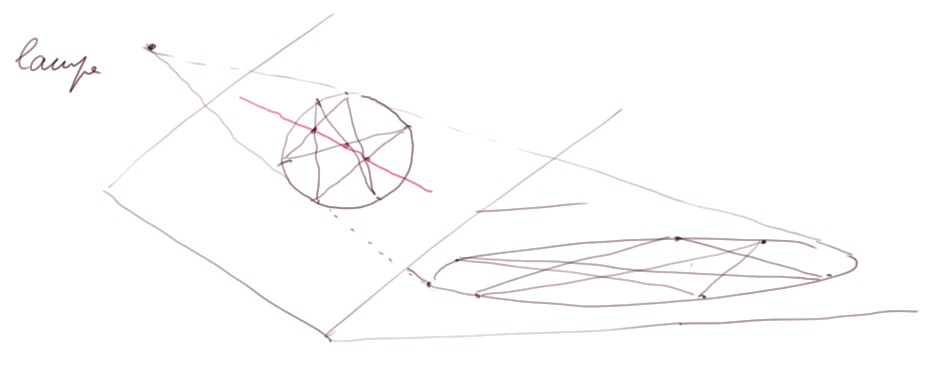
Les cercles deviennent des coniques, les droites restent des droites.
Il y a une merveilleuse propriété des cercles, démontrée par Pascal, au XVIIe siècle : prenez un cercle et six points quelconques sur le cercle, tracez les six segments AE, AF, BD, BF, CD et CE qui relient les points deux à deux comme sur la figure ci-dessous. Alors les trois points d'intersection, deux à deux, sont alignés (droite rouge).
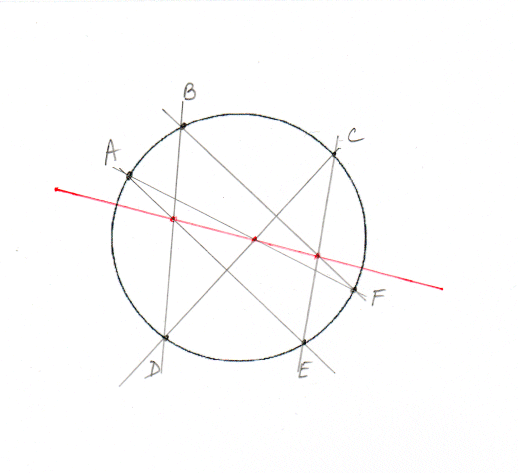 |
Et comme les projections dans l'espace à partir d'un point, depuis un plan vers un autre, conservent les droites et transforment les cercles en coniques, cette propriété est vraie pour toute conique. Elle est même vraie pour une conique très particulière : deux droites qui se coupent. Si on prend trois points A, B et C sur l'une des droites, trois points D, E et F sur l'autre, et qu'on trace les segments AE, AF, BD, BF, CD et CE, alors les trois points d'intersection montrés ci-dessous sont alignés. Je vous engage à prendre une feuille de papier, un règle et un crayon, et à vérifier par vous-même avec un exemple.
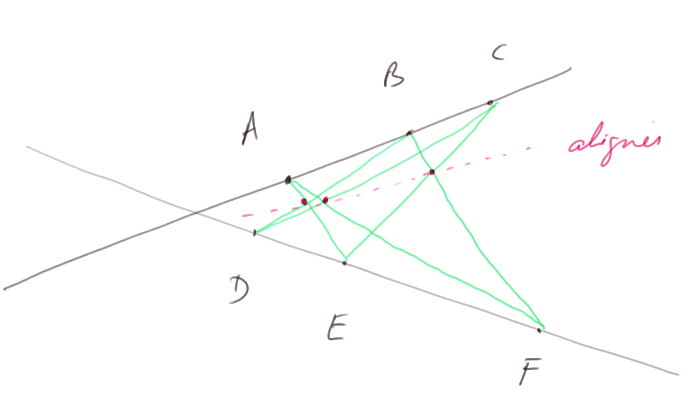
Ce théorème était déjà connu des Grecs au quatrième siècle avant J.-C.
A vrai dire, nous voilà revenus à de la géométrie dans le plan. Mais la géométrie dans le plan et la géométrie dans l'espace sont très liées.
Enfin, comme on a étudié les longueurs sur la droite, et les surfaces dans le plan, nous étudierons les volumes dans l'espace, et aussi les surfaces extérieures de formes dans l'espace (par exemple le volume et la surface d'une sphère).
Exercices
- Combien de cubes de 1 mètre de côté, je peux mettre dans un cube de 2 mètres de côté ?
- Quelle est la surface extérieure complète d'un cube de 2 mètres de côté ?
Plan général du cours
Contacter le professeur
Réponses :
- Combien de cubes de 1 mètre de côté, je peux mettre dans un cube de 2 mètres de côté ? Réponse : 8
- Quelle est la surface extérieure complète d'un cube de 2 mètres de côté ? Réponse : 24 m2