Cours de mathématiques de 6e24. La géométrie dans le plan |
|
|
|
|
Video |
|
Texte
Un plan c'est la surface d'une table, d'un parquet, d'un mur, d'une feuille de papier, de cet écran que vous regardez. Le plan a une propriété intéressante : c'est la forme que prend l'interface entre deux objets quand on les frotte l'un contre l'autre dans tous les sens.
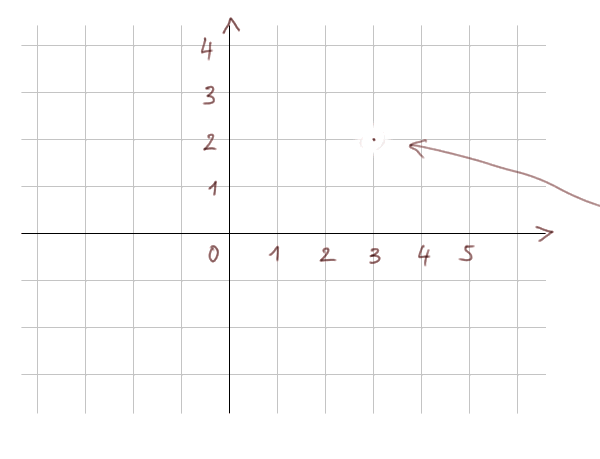
Parfois on regardera ce plan nu, parfois on le regardera équipé d'un repère (comme ci-dessous).

Un repère, comme son nom l'indique, permet de repérer des points du plan. Les 2 droites plus noires s'appellent les axes. Leur intersection s'appelle l'origine. Le point (3 ; 2) est le point qui abaissé sur l'axe horizontal est à la marque 3, et glissé vers l'axe vertical est à la marque 2.
Dans le plan nu, ou avec un repère, on étudiera les droites : droites qui se coupent, droites parallèles (voir vidéo pour toutes les figures).
Les triangles : figures formées par trois points et les segments qui les relient.
Types de triangles : quelconque, isocèle, équilatéral, rectangle.
Les quadrilatères : figures formées par quatre points et les segments qui les relient pour faire une figure fermée. En général on se cantonne à celles non croisées. Attention : un quadrilatère dans l'espace peut ne pas être dans un plan, comme un "cadre faussé". Alors qu'un triangle est toujours dans un plan.
Types de quadrilatères : parallélogramme, rectangle, carré, losange, autres.
Et encore : les cercles, les angles, les surfaces, etc.
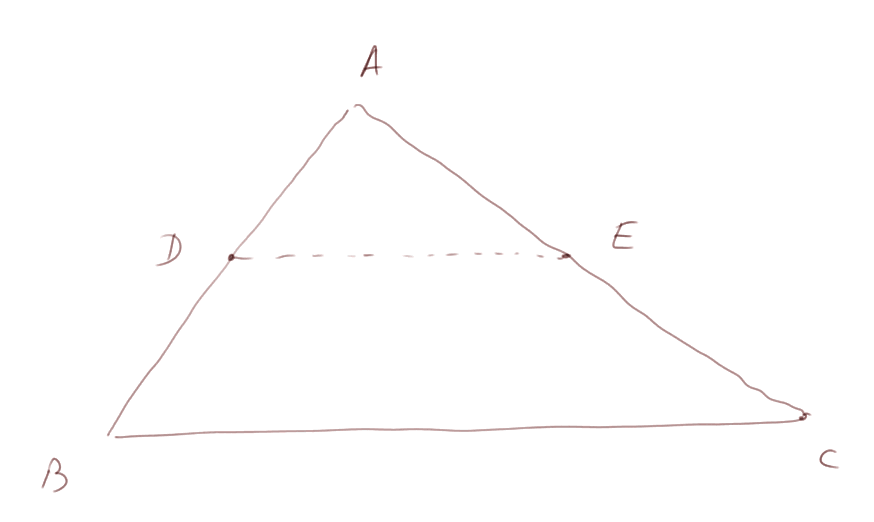
Nous rencontrerons beaucoup de propriétés intéressantes. Exemple 1 : dans un triangle quelconque, ABC, si D est le point au milieu de AB, et E le point au milieu de AC, alors le segment DE est parallèle à BC, et il est de longueur exactement moitié.
Exemple 2 : un triangle peut toujours être inscrit dans un cercle (ce n'est pas le cas d'un quadrilatère, qui peut l'être ou pas). Si l'un des côtés du triangle est un diamètre du cercle, alors le triangle est forcément rectangle. La réciproque est vraie aussi : si le triangle est rectangle, alors un de ses côtés est un diamètre du cercle dans lequel le triangle est inscrit.
Exercice
- Si, dans le triangle ABC ci-dessus, je recoupe AB en deux avec un point M milieu de AD, et je recoupe AC en deux avec un point N milieu de AE, quelle sera la longueur de MN ?
Plan général du cours
Contacter le professeur
Réponse : un quart de la longueur BC.