Cours de mathématiques de 6e17. Les nombres premiers |
|
|
|
|
Video |
Tout nombre entier n est évidemment égal à n x 1. Donc tout nombre entier n est un multiple de 1 et de lui-même.
Les nombres qui ne sont multiples d'aucun autre nombre que 1 et eux-mêmes s'appellent les nombres premiers.
12 n'est pas premier, car il est multiple de 3 (et de plusieurs autres nombres). 7 est premier.
Si l'on assimile les nombres à des collections de petits cailloux (comme le mot "calcul" nous le rappelle), les nombres premiers sont ceux qu'on ne peut pas ranger en rectangle de plusieurs rangées identiques.

est premier : pas moyen de ranger ces sept petits cailloux en plusieurs rangées identiques.
Le nombre ci-dessous

en dépit des apparences n'est pas premier, car c'est aussi

En d'autre termes 21 = 3 x 7.
Le début de la liste des nombres premiers est
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
etc. |
(il est d'usage de ne pas compter le nombre 1 dans les nombres premiers).
Les nombres premiers jouent un rôle étonnamment important en mathématiques. On verra que ce sont en quelque sorte les "briques élémentaires" de tous les nombres. Certains résultats concernant les nombres premiers sont faciles à prouver, d'autres sont difficiles, et d'autres ne sont pas encore résolus.
Par exemple : il y a une infinité de nombres premiers. C'est un résultat relativement facile à démontrer. Nous y reviendrons en classe de seconde.
Deuxième exemple : dans la suite des nombres premiers, il y a vraisemblablement une infinité de paires de nombres séparés par 2, comme 3 et 5, 5 et 7, 11 et 13, 17 et 19, 29 et 31, 41 et 43, 59 et 61 etc. Les mathématiciens pensent que c'est vrai mais ne savent pas le démontrer. Ce n'est donc qu'une conjecture.
Digression : Ça veut dire quoi "démontrer" ? Ça veut dire construire un raisonnement suivant des règles strictes de déduction au terme duquel on parvient à la véracité de la conjecture sur laquelle on travaille. Ainsi pour démontrer que Socrate est mortel, on part de l'axiome que tout homme est mortel, puis on considère le fait que Socrate est un homme, alors on en déduit que Socrate est mortel. Une démonstration doit être une chaîne finie de signes. Une chaîne infinie ne convient pas.
Il existe en arithmétique des conjectures, dont la formulation est relativement simple, pour lesquelles on a démontré en 1970 qu'il n'y avait pas de démonstration ! Ce sera peut-être le cas de la conjecture sur les paires de nombres premiers séparés par deux. C'est-à-dire qu'il est possible que la série des paires de nombres premiers séparés par deux ne s'arrête jamais, mais qu'il n'existe pas de démonstration (de raisonnement avec un nombre fini d'étapes) qui l'établisse. Bref, quelque chose de vrai mais indémontrable.
Avant qu'on ne finisse par démontrer, au terme de 350 ans d'efforts, le grand théorème de Fermat (pour n quelconque plus grand que 2, il n'existe pas de triplets d'entiers [x, y, z], où aucun n'est nul, satisfaisant xn + yn = zn), certains mathématiciens avaient commencé à supputer que c'était peut-être un de ces énoncés arithmétiques indémontrables. Finalement, il a été démontré en 1995 que cette conjecture-là était vraie. Depuis on a aussi démontré que la plupart des énoncés arithmétiques n'étaient pas démontrables.
Pour aller plus loin : les paires de nombres premiers séparés par 2, dixième problème de Hilbert, et le théorème de Green et Tao.
Les nombres premiers sont de plus en plus espacés en moyenne quand on avance vers les grands nombres.
Ils sont désarçonnants, car ce sont les nombres qui sont "un peu étranges", qui ne sont pas réguliers comme un rectangle, qui sont "spéciaux".
Par définition ils n'apparaissent pas dans la table de multiplication (à part dans la première ligne et la première colonne à fond blanc) :
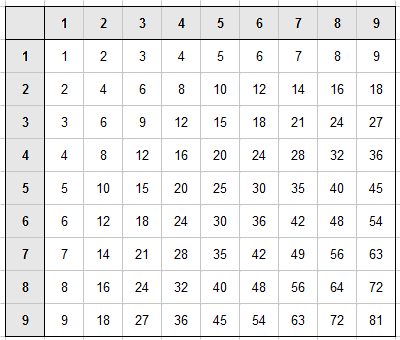
Et pourtant ils présentent d'autres formes de régularité : par exemple leur densité moyenne entre 0 et n'importe quel nombre N est connue, même si eux-mêmes ne le sont pas bien !
Spirale d'Ulam : Les nombres premiers ont donc beaucoup de propriétés étranges. Il faudrait des volumes pour parler de toutes celles intéressantes, alors citons seulement la spirale d'Ulam.
Disposer tous les nombres dans une spirale comme ceci :

disposition initiale de tous les nombres dans la spirale d'Ulam
(source : wikipedia)
Puis effacer tous les nombres non premiers, et replacer les nombres premiers par des points de taille fixe.
Quand on réalise ce dessin avec un grand nombre de nombres (par exemple jusqu'à n = 100 000) on obtient une figure qui montre d'étranges "lignes de forces" horizontales, verticales et à 45° suggérant une structure qui devrait être facile à expliquer.

mystérieuses lignes horizontale, verticales et à 45°
(cliquer sur l'image pour la voir en plus grand)
Jusqu'à présent (juin 2016) l'explication de ces lignes défie les mathématiciens.
Exercices
- Est-ce que 100 est premier ?
- Est-ce que 101 est premier ? (Suggestion : si 101 n'est pas premier, alors 101 = p x q, où p ou q est inférieur ou égal à 10, donc essayer seulement de diviser par les nombres de 2 à 10. Ce n'est pas la peine d'aller plus loin.)
- Dans l'exercice précédent, est-ce nécessaire d'essayer de diviser par 4, par 6, par 8, par 9, par 10 ?

Plan général du cours
Contacter le professeur
Réponses
- Est-ce que 100 est premier ? Réponse : non, c'est divisible par 2 et par 5, et par d'autres nombres.
- Est-ce que 101 est premier ? Réponse : oui.
- Si on a déjà essayé de diviser par 2 et que ça ne marchait pas, ce n'est pas la peine d'essayer de diviser par 4, car si 101 était divisible par 4 il le serait aussi par deux. Même raisonnement avec 6, 8, 9 et 10. Si 101 était divisible par 10, il le serait aussi par 2 et par 5.