Cours de mathématiques de 6e33. Patrons et volumes |
|
Video |
Texte
Pour développer notre perception dans l'espace, nous allons faire quelques pliages. Un cube peut être fabriqué, avec du carton et de la colle, par pliage.
Le dessin initial s'appelle un patron. Plusieurs patrons différents mènent au même cube (écran 3).
Certains patrons ne marchent pas. Avec le patron ci-dessous, en repliant, la face 6 va aller sur la face 2. Et le cube aura une face vide.
On peut faire le patron d'un parallélépipède rectangle (écran 5).
Il y a quelques contraintes sur les côtés du patron : les segments marqués avec deux petites barres doivent être égaux.
On peut faire le patron d'une pyramide (écran 6).
On ne peut pas faire par pliage d'une feuille de papier une sphère.
Ce n'est pas la "rondeur" de la sphère qui est le problème. On peut faire par pliage des formes qui ont des "rondeurs", par exemple un cône (écran 8).
On peut faire le patron d'un cylindre (écran 9).
On peut faire des polyèdres. Polyèdre = forme dans l'espace avec plusieurs faces. Un cube est un polyèdre régulier à 6 faces. On peut faire un dodécaèdre (= polyèdre régulier à 12 faces).
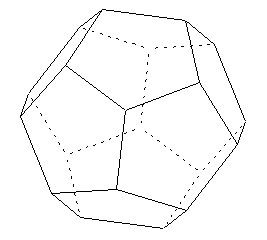
(Source : www.bibmath.net)
Chaque face est un pentagone, c'est-à-dire un dessin dans le plan avec 5 côtés.
Exercice
-
Combien y a-t-il de faces sur le ballon de football ci-dessous ?

- Voyez-vous que ce ballon de foot est un icosaèdre (un polygone régulier à 20 faces triangulaires) dont tous les sommets ont été tronqués ?