Cours de mathématiques de 6e35. Représentations graphiques |
|
|
|
|
Video |
|
Texte
"Une image vaut mille mots." (proverbe chinois).
On peut aussi dire que souvent une représentation graphique d'une série de nombres aide à mieux les percevoir et à les comprendre.
En 2007 la population mondiale par continent était : Asie 4,03 milliards, Afrique 965 millions, Europe 731 millions, Amérique latine 572 millions, Amérique du Nord 339 millions et Océanie 34 millions.
En ayant seulement lu ces nombres, on peut ne pas avoir pris la mesure réelle de l'importance prépondérante de l'Asie dans la population mondiale.
Pour rendre ces nombres plus "parlants", les voici représentés avec des barres verticales.
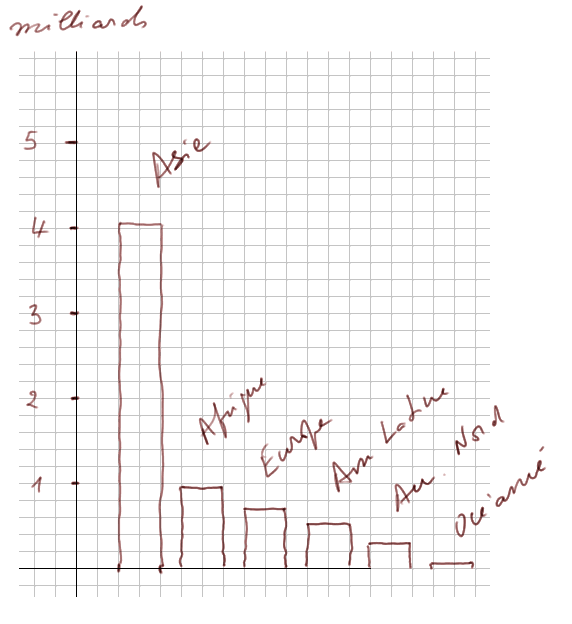
Force est de reconnaître que ce dessin parle plus que les seuls nombres des populations par continent.
Une autre représentation courante est "en camembert". On représente la population de chaque continent comme une portion de camembert qui lui est proportionnelle. Pour cela on calcule d'abord les pourcentages. La population totale était 6671 millions. Donc l'Asie représentait 60,4%, l'Afrique 14,5%, l'Europe 11,0%, l'Amérique latine 8,6%, l'Amérique du Nord 5,1% et l'Océanie 0,5%.
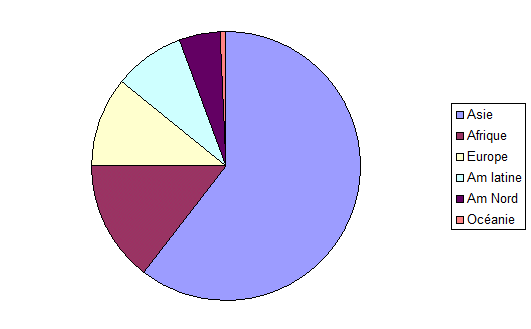
Etudions maintenant un randonneur qui marche entre 8 heures du matin et 14 heures, et sa vitesse moyenne chaque heure. Première heure : 6 km/h. Deuxième heure : 6. Troisième heure : 5. Quatrième : 0. Cinquième : 4. Et sixième : 5 km/h.
On peut représenter graphiquement sa vitesse moyenne en fonction de l'heure.
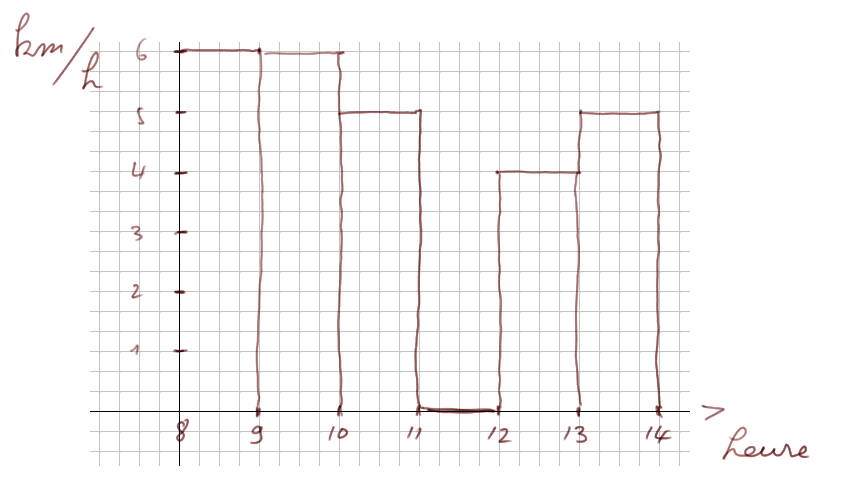
C'est Nicolas Oresme (c. 1325, 1382) qui au XIVe siècle a le premier utilisé cette représentation d'une série de nombres (ici une vitesse moyenne chaque heure) en fonction d'une autre série de nombres (ici les heures).
Il a d'ailleurs fait une remarque fort intéressante : la surface de l'ensemble des barres représente la distance totale parcourue. Ici : 26 kilomètres.
Si une voiture roule à 50 km/h, on peut regarder le trajet parcouru pour différentes durées. Et on peut représenter le trajet en fonction de la durée.
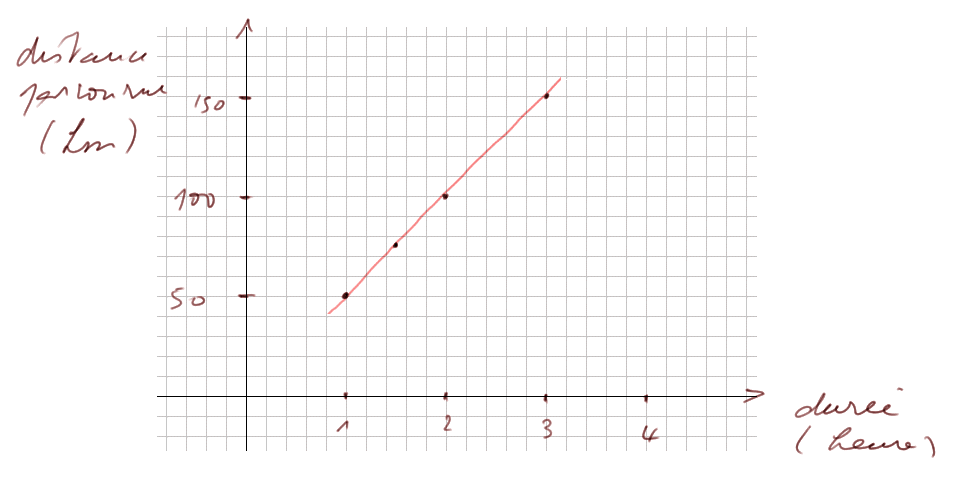
On voit que les points sont alignés sur une droite.
Enfin, intéressons-nous à la relation entre la surface d'un carré et la longueur de son côté.
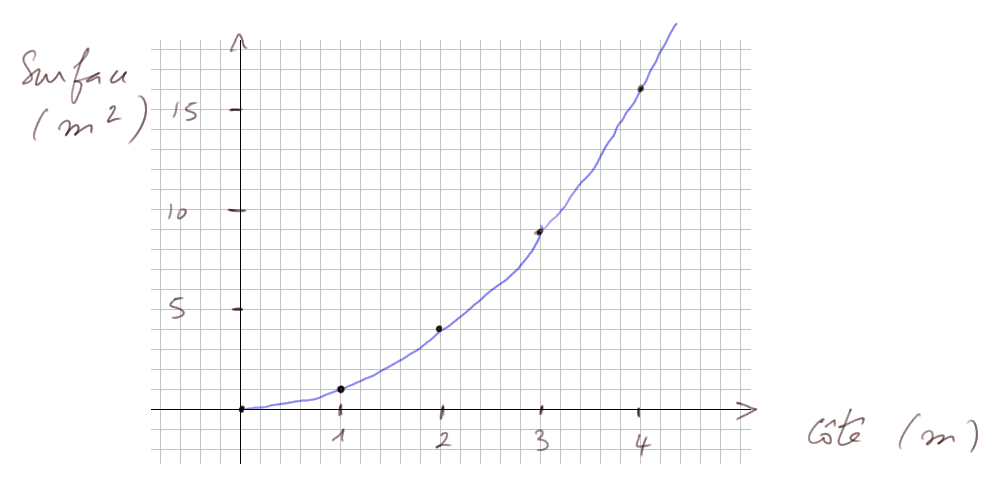
Ici les points ne sont pas sur une droite. Ils sont sur une parabole. (On a déjà rencontré brièvement les paraboles quand on a étudié l'intersection entre un plan et un cône.)
Exercice
- Quelle est la surface d'un carré de 1,5 mètre de côté ?
- Positionner le point correspondant sur le graphique ci-dessus.
Plan général du cours
Contacter le professeur
Réponses :
2,25 m2.
Le point est sur la courbe bleue, entre les points correspondants aux marques horizontales 1m et 2m.