Cours de mathématiques de 6e6. La soustraction |
|
|
|
|
Video |
La soustraction est comparable à l'addition en terme d'absence de difficulté particulière. Elle ne présente qu'une différence : on ne peut pas soustraire plus que le nombre initial.
Soustraire 27 de 75, consiste à partir d'une collection de 75 objets, en enlever 27, et compter combien il en reste. On peut le calculer de tête de différentes manières, par exemple : 75 - 27 = 75 - 25 - 2 = 50 - 2 = 48.
Nous allons étudier le procédé général de la soustraction comme nous avons étudié celui de l'addition. De même que pour l'addition , le système de notation des nombres avec les chiffres arabes permet d'effectuer les soustractions de manière mécanique.
Il faut connaître sa table des soustractions élémentaires. Elle est un petit peu plus compliquée que celle des additions.
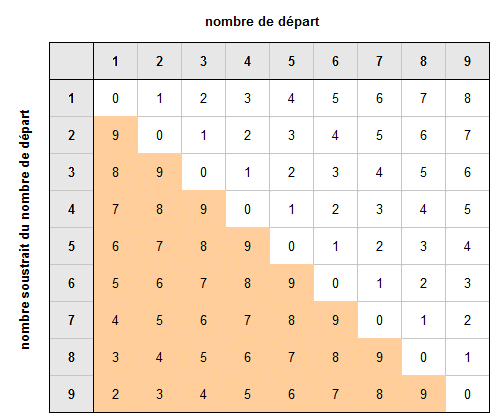
table de soustraction
Dans la zone orangée on doit retirer un chiffre plus grand que le chiffre de départ. Pour contourner cette difficulté on procédera de la manière suivante : on ajoute 10 au chiffre auquel on va soustraire un autre chiffre, et on "retiendra" 10 à ajouter au chiffre qui est soustrait, c'est-à-dire 1 au chiffre qui est à sa gauche (pour se conformer à la représentation des nombres selon le système arabo-hindou).
Pour bien comprendre cette petite astuce, la vidéo illustre par un exemple comment on procède pour calculer par exemple 782 - 164 = 618
Le mécanisme consiste à ajouter 10 au 2 de 782 pour pouvoir retirer 4, puis à rajouter 10 en bas à 164, c'est-à-dire 1 au 6. Ainsi la soustraction reste correcte.
Une autre différence : c'est naturel d'additionner d'un seul coup plusieurs nombres, mais ça ne l'est pas de soustraire d'un seul coup plusieurs nombres d'un nombre donné : poser la soustraction n - p - q - r n'est pas naturel. On commencera plutôt par faire la somme de tous les nombres qu'on veut soustraire : m = p + q + r, et puis on soustraira leur somme m du nombre initial n. En d'autres termes, les soustractions manuelles sont seulement l'opération n - m, où m est plus petit ou égal à n.
Nous avons vu que l'addition de deux nombres n et m peut se représenter sur une demi-droite comme le déplacement, à partir de la position n, de m pas vers la droite. La marque sur laquelle on arrive est le résultat de n + m. Dans le cas de la soustraction n - m, on part de la marque n, et on se déplace de m pas vers la gauche, on arrive sur la marque correspondant à n - m.
Comme l'addition, la soustraction est une opération qui à une paire ordonnée de nombres en fait correspondre un troisième. Mais on ne peut pas soustraire à un nombre entier plus que lui-même. Donc la soustraction ne marche pas sur toutes les paires ordonnées de nombres entiers, alors que c'était le cas avec l'addition. Et avec l'addition l'ordre dans la paire n'était pas important : 5 + 7 et 7 + 5 donnent la même chose.
On verra plus tard que la soustraction est en fait considérée comme la même opération que l'addition : 7 - 3 est simplement 7 + (-3) où -3 est un nouveau nombre décrit plus bas.
Dans la représentation avec une demi-droite, on voit que si on cherchait à soustraire de n un nombre m plus grand que n, on serait conduit à dépasser l'origine. Dans un cours ultérieur on verra qu'on peut prolonger la demi-droite vers la gauche après l'origine et en faire une droite complète sur laquelle on rajoutera aussi des marques. Elles correspondront à des nouveaux nombres, qui ne font pas partie de la collection 0 1 2 3 4 5 6 7 8 9 10 11 12 etc. Ces nouveaux nombres ne serviront pas à compter des œufs dans un panier. Mais ils auront d'autres usages : repérer des positions géographiques sur une ligne, mesurer une profondeur sous l'eau, exprimer des dettes vis-à-vis de quelqu'un d'autre, et d'autres choses encore.
Par exemple, vous avez prêté 3 euros à un ami, et le lendemain il vous rembourse, mais comme il n'a pas de monnaie, il vous donne un billet de 5 euros. Si les 3 euros correspondaient à la position 3 sur la demi-droite vers la droite, où sommes-nous quand on doit maintenant 2 euros à l'ami ? (Vous étiez créancier de 3 euros, vous êtes maintenant débiteur de 2 euros.)
En bleu : évolution de ma "position financière" quand je prête 3. En rouge : évolution de ma "position financière" quand on me rembourse 5.
Pour vous entraîner, faites quelques soustractions avec la page suivante :
Ces nombres à la gauche du zéro s'appellent les nombres négatifs. Si on cherche à les "sentir" comme on peut sentir trois ou vingt-sept, on n'arrive à rien. Ce ne sont plus des nombres représentant des quantités matérielles concrètes comme deux maisons ou une portée de cinq chats. Quelque chose de translucide ou retourné comme un gant est une mauvaise image. Mieux vaut encore y penser comme à des notations obéissant à des règles.
Encore une fois, une bonne représentation des nombres négatifs sont des dettes comparées à des avoirs (qui eux correspondent à des nombres ordinaires, dits aussi positifs).
En fait ce sont des toutes premières "créatures mathématiques" un peu abstraites. On verra cependant qu'on devient très vite à l'aise avec les nombres négatifs, comme avec les boutons de l'ascenseur dans une tour qui a un rez-de-chaussée (correspondant au nombre zéro) trente étages et cinq sous-sols.
Si les nombres négatifs vous effraient, sachez qu'ils ont perturbé les mathématiciens – pas les plus grands néanmoins – pendant plusieurs siècles (de 1100 à 1500 environ).
Plus tard, d'autres "créatures mathématiques" plus abstraites, les nombres complexes (appelés aussi nombres imaginaires), ont aussi perturbé les mathématiciens pendant plusieurs siècles (de 1550 à 1850 environ). Une des façons de se familiariser avec les nombres complexes était de se rappeler que les nombres négatifs avaient longtemps paru très étranges eux aussi. Finalement tous les mathématiciens et tous les utilisateurs des mathématiques sont devenus très à l'aise avec les nombres complexes. Ils servent énormément dans de nombreuses branches des mathématiques, de la physique, de l'électricité et du magnétisme, etc.
Les mathématiciens et les physiciens se sentent libres d'inventer toutes sortes d'objets pour décrire des situations de la vie quotidienne. Ils ne sont pas limités à ce qui est "évident".
Parfois les nouveaux concepts sont introduits par les mathématiciens et utilisés plus tard par les physiciens et les ingénieurs, par exemple les nombres imaginaires ou les structures de groupe. Parfois ils sont introduits par les physiciens ou les ingénieurs et ajoutés plus tard par les mathématiciens dans la boîte à outil officielle, par exemple les distributions ou les ondelettes.
Comment peser son chat ? Cédric veut peser son chat sur le pèse-personne de la salle de bain, mais son chat ne veut pas rester sur la balance. Alors Cédric a l'idée de se peser avec son chat dans les bras. La balance indique 31 kilogrammes. Puis il se pèse sans son chat. La balance indique 26 kilogrammes. Quel est le poids de son chat ?
Plan général du cours
Contacter le professeur
Réponse : 31 - 26 = 5 kg