Cours de mathématiques de 6e26. Surfaces et aires |
|
Video |
Texte
IntroductionDans le plan, on appelle "surface" une partie du plan :
- un rectangle et son intérieur (pensez à un champ à la campagne)
- un cercle et son intérieur (appelé parfois un disque)
- une forme quelconque et son intérieur.
On appelle "aire" la dimension d'une surface. Evidemment, qu'est-ce qu'on veut dire par "dimension" ?
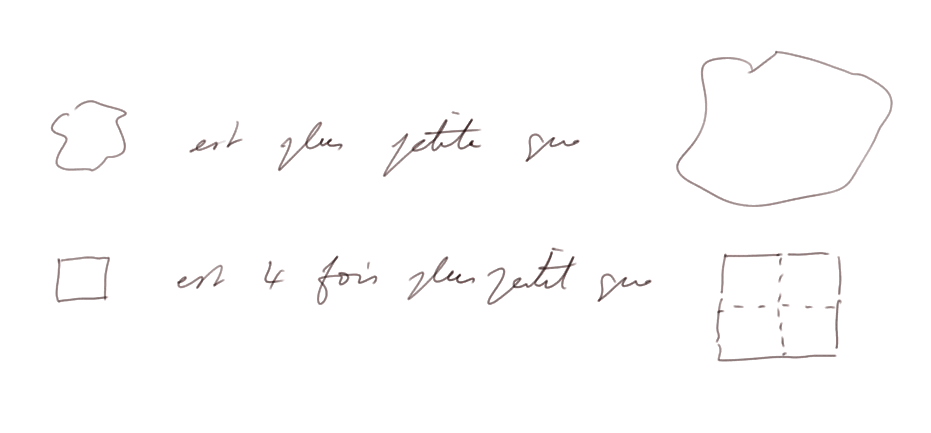
Elle remonte au moins aux paysans égyptiens du troisième millénaire avant J.-C. Ils exploitaient des champs le long du Nil pour faire pousser des céréales et d'autres plantes. Chacun avait le sien, balisé par des piquets et des barrières. Eudème de Rhodes, un disciple d'Aristote, a rapporté le problème qu'ils rencontraient : chaque année la crue du Nil, qui apportait le précieux limon fertilisant, effaçait aussi tous les repères des champs, et après la crue il fallait redessiner le champ de chacun. Les arpenteurs (appelés du joli nom d'harpédonaptes) et les paysans avaient bien compris qu'il n'était pas très important que chaque nouveau champ ait exactement la même forme au même emplacement que l'année précédente, pourvu qu'une certaine mesure du champ reste la même qu'avant. Car la quantité de leur récolte était proportionnelle à cette mesure qu'ils percevaient confusément.
Quelle mesure ? La longueur du pourtour ? Les plus perspicaces avaient compris que ce n'est pas parce qu'un champ avait un pourtour plus grand qu'il était préférable. Par exemple un rectangle de 100m par 30m a un pourtour plus long qu'un carré de 60m par 60m, néanmoins ils savaient que le carré était "mieux". Pourquoi ? Quel était donc ce nombre (cette "mesure") attaché au carré, qui était supérieur au nombre attaché au rectangle ?
C'est ainsi qu'ils ont compris que c'était quelque chose qu'on appelle en français l'aire (en anglais "surface area"). Et la définition de l'aire est l'objet de notre leçon.
L'aire d'un carré de 1 mètre de côté est appelée "un mètre carré" et est notée 1 m2. L'aire d'un carré de 1 centimètre de côté est appelée "un centimètre carré" et est notée 1 cm2. Il y a 10 000 cm2 dans 1 m2.
On appelle aire d'un rectangle (en m2) le nombre de fois qu'on peut y faire tenir un carré de 1 m2 complet, éventuellement découpé.
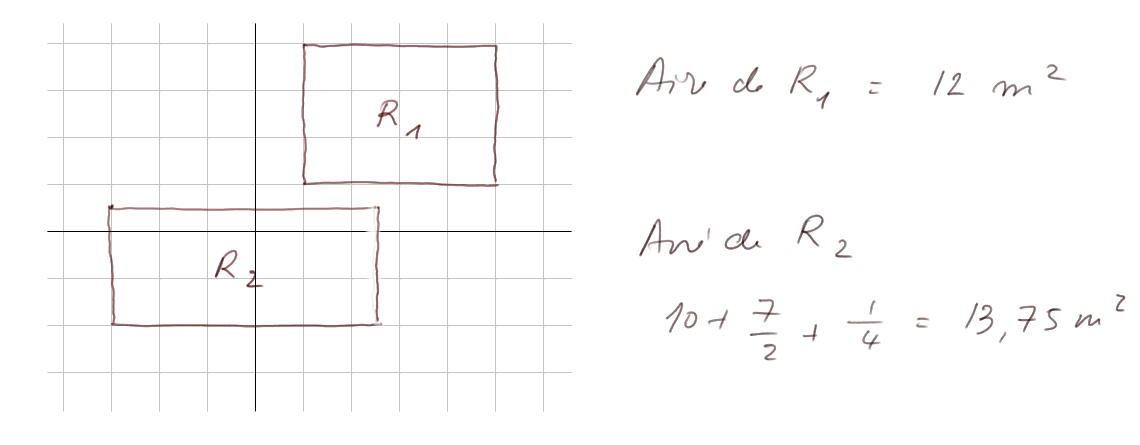
L'aire d'un rectangle (en m2) est le produit de sa longueur (en mètre) par sa largeur (en mètre). Un rectangle de 5,5 m par 2,5 m a une aire de 13,75 m2.
Pour se convaincre que la longueur (en mètre) multipliée par la largeur (en mètre) d'un rectangle donne bien "le nombre de fois qu'on peut mettre un carré complet de 1 m2 dedans", observons que si la longueur et la largeur sont des nombres entiers de mètre, c'est juste la représentation de la multiplication avec du carrelage comme nous l'avons déjà rencontrée dans la leçon "Les nombres et leurs représentations (2) : rectangles de petits cailloux et carrelages".
Dans le cas où la longueur et la largeur sont des fractions, par exemple longueur = 5, 5 = 5 + 1/2, et largeur = 2,5 = 2 +1/2. Alors (5 + 1/2) x (2 + 1/2) = 10 carrés complets + 5 demi carrés + 2 demi carrés + 1 quart de carré. C'est donc bien encore le nombre de carrés complets ou équivalents, plus une portion de carré, qu'on peut mettre dans le rectangle. Le même raisonnement s'étend aisément à deux fractions quelconques.
Si une surface S est la somme de deux surfaces plus petites, qui ne se chevauchent pas, alors l'aire de S est la somme des aires des deux petites surfaces.
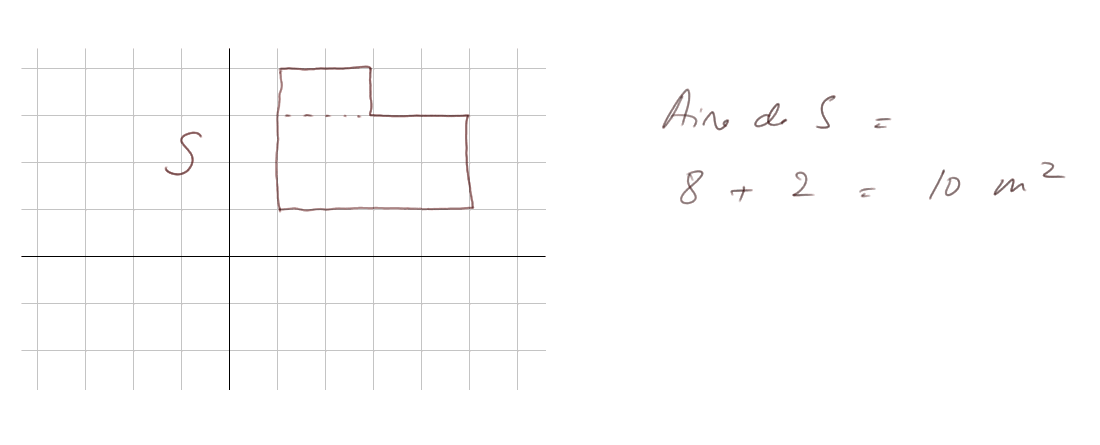
Triangles
Cela nous conduit naturellement à l'aire d'un triangle. On commence par un triangle rectangle. On voit qu'il est la moitié d'un rectangle. Donc son aire est la moitié de l'aire du rectangle dans lequel tient le triangle.

Pour un triangle quelconque, on commence par tracer le point H tel que AH est perpendiculaire à BC.
AH s'appelle la "hauteur" du triangle correspondante à BC. Alors on voit que le triangle ABC est constitué de deux triangles rectangles : ABH et AHC. Chacun a pour aire la moitié du rectangle dans lequel il tient. Ces deux rectangles, DAHB et AHCE, forment le rectangle DBCE. Donc le triangle ABC a pour aire la moitié du rectangle. Aire de ABC = (1/2) x BC x AH.
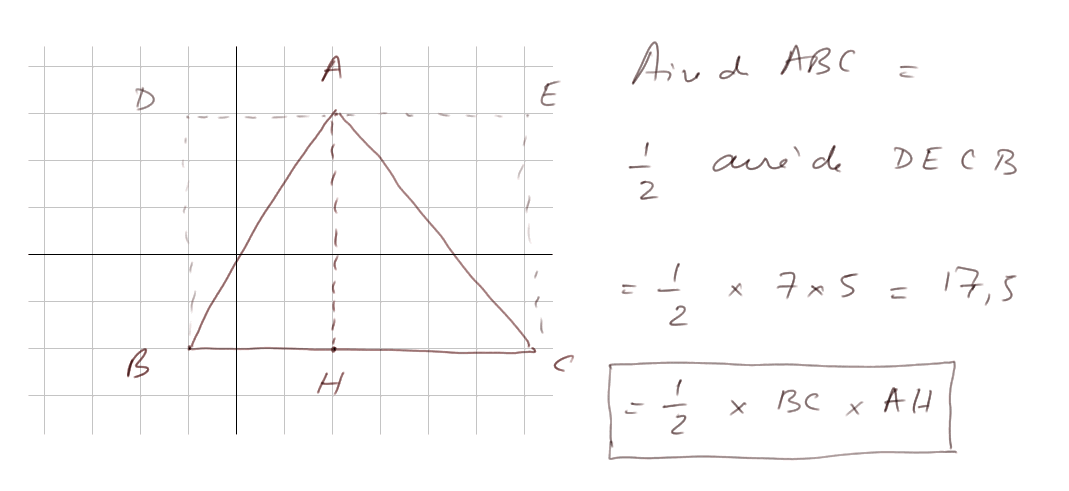
Formule à retenir : l'aire d'un triangle est la longueur de sa base multipliée par sa hauteur divisée par 2.
Comme on peut faire ce calcul avec n'importe lequel des trois côtés du triangle et sa hauteur correspondante, et qu'on tombe forcément sur la même aire, ça devient une propriété des triangles : les 3 produits, côté x hauteur correspondante, sont égaux.
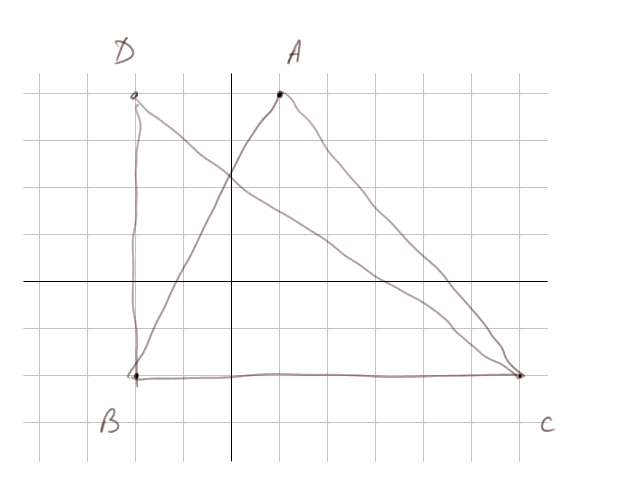
Terminons par une façon amusante de voir l'aire d'un triangle. Prenons un triangle quelconque ABC et le triangle rectangle DBC obtenu en faisant glisser A parallèlement à BC afin qu'il se positionne juste au dessus de B
 .
.
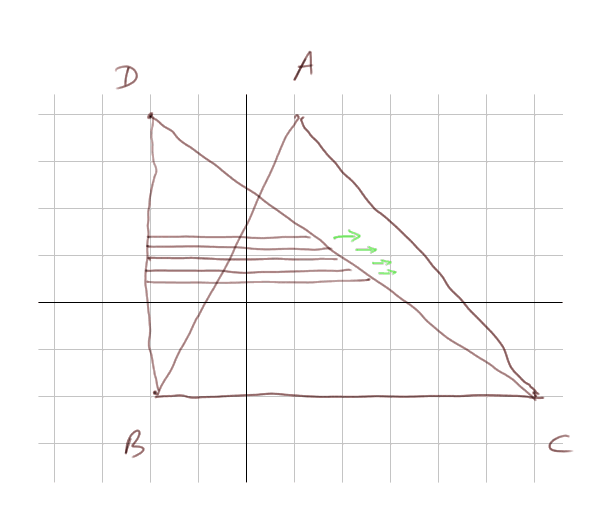
L'aire de DBC est (8 x 6) / 2 = 24 m2. On peut découper DBC en fines tranches horizontales qui sont presque des rectangles très allongés et très minces. L'aire de DBC est la somme des aires de ces fines tranches.
On peut faire glisser ces fines tranches vers la droite pour recréer le triangle ABC. Comme la somme des aires des fines tranches ne change pas, l'aire de ABC est égale à l'aire de DBC. Nous rendrons cette "démonstration" indiscutable pour tard.
- Sur une feuille de papier quadrillée à petits carreaux, tracez un repère avec l'unité 1 cm.
- Tracer le rectangle formé des quatres points A = (1 ; 2), B = (8 ; 2), C = (8 ; 5) et D = (1 ; 5).
- Quelle est l'aire du rectangle ? (Rappel : un point A = (n ; m) se positionne, dans un repère, sur la verticale qui coupe l'axe horizontal en n, et sur l'horizontale qui coupe l'axe vertical en m.
- Montrer que l'aire du triangle ci-dessous est 9 cm² ? (On fera l'hypothèse que chaque petit carreau fait 1 cm² ; le dessin les représente avec une taille réduite.)
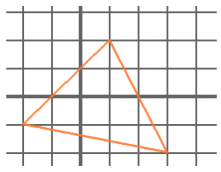
- Considérons un triangle quelconque dont les trois sommets ont chacun des coordonnées entières (c'est-à-dire sont sur les croisements du quadrillage ci-dessus). Montrer que le double de son aire est forcément un multiple entier de la surface d'un petit carré. (En d'autres termes, si les carrés ont par exemple l'aire 1 cm², le double de la surface du triangle est toujours un nombre entier de cm².)
Plan général du cours
Contacter le professeur
Réponse à la question 3 : 21 cm2
Pour la question 4 : regarder l'aire du rectangle à côtés horizontaux et verticaux dans lequel est inscrit le triangle, et enlever l'aire des 3 triangles rectangles qui bordent le triangle orangé.