Cours de mathématiques de 6e28. Symétries |
|
Video |
Texte
On distingue deux sortes de symétries dans le plan : la symétrie par rapport à une droite, et la symétrie par rapport à un point.
La symétrie par rapport à une droite D, c'est une transformation qui à tout point P du plan fait correspondre un point Q, de l'autre côté de la droite D, tel que la droite coupe le segment PQ en son milieu, et soit perpendiculaire à PQ.

Alors à toute figure correspond une autre figure.
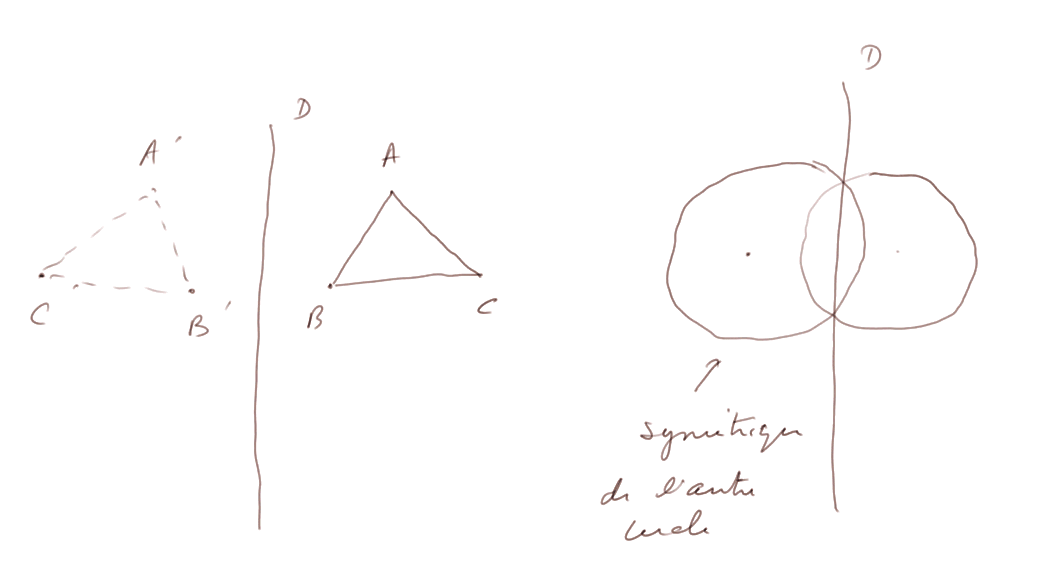
La symétrie par rapport à une droite ne change aucune longueur. Par cela on veut dire que, si A' est le symétrique de A, et B' est le symétrique de B, alors la longueur du segment A'B' est la même que la longueur du segment AB.
On ne va pas se préoccuper de "démontrer" cela. Contentons-nous d'observer qu'on peut voir la symétrie en "repliant" le demi-plan à droite sur le demi-plan à gauche, le pli étant le long de la droite D. Alors on peut voir "en transparence" à gauche la symétrique d'une figure qui était dessinée à droite.
"Démontrer" veut dire "déduire logiquement" à partir de résultats précédents, eux-mêmes déduits de résultats encore précédents... Au départ, il y a juste quelques "objets mathématiques fondamentaux" et des règles. C'est une discipline particulière des mathématiques, qui cherche à se dégager des représentations pour se concentrer sur la logique. (Ainsi aux échecs, il y a des pièces et des règles de déplacement sur des cases, et peu importe si les cavaliers ressemblent à des chevaux, si la reine a une couronne, etc. On peut même jouer dans sa tête sans la représentation traditionnelle d'un échiquier.) On n'étudiera pas cela.
Les joueurs de billards utilisent beaucoup la symétrie par rapport à une droite. Avec une bille bleue, pour viser une bille rouge, après rebond sur un bord, ils visualisent dans leur tête la symétrique de la rouge par rapport au bord, et visent cette bille virtuelle. Grâce au rebond qui produit la symétrique de ce qu'aurait été la trajectoire de la bille bleue s'il n'y avait pas eu de bord, la bille bleue arrive à la vraie bille rouge.
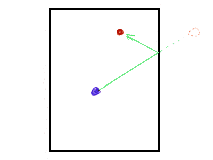
Comment les joueurs de billard utilisent la symétrie par rapport à une droite
La symétrie par rapport à une droite ne change qu'une chose : le sens de parcours d'un périmètre. Si pour parcourir ABC on tourne dans le sens des aiguilles d'une montre, alors pour parcourir A'B'C' on tourne dans le sens inverse.
(La symétrie par rapport à une droite ne change pas les angles, mais change leur sens de parcours pour aller d'un côté à l'autre.)
Symétrie par rapport à un point. On a un point central O, qui sera le "centre de symétrie". Alors à chaque point A on fait correspondre un point A' tel que O soit le milieu de AA'.

La symétrie par rapport à un point ne change pas les distances, et même pas les sens de parcours des figures. En fait c'est tout simplement comme faire tourner sa feuille de 180° par rapport au centre de symétrie.
Exercices
- Est-ce que le symétrique d'un triangle par rapport à une droite peut être un rectangle ?
- Est-ce que la symétrie par rapport à une droite change les aires ?
Plan général du cours
Contacter le professeur
Réponses
- Est-ce que le symétrique d'un triangle par rapport à une droite peut être un rectangle ? Rép : non.
- Est-ce que la symétrie par rapport à une droite change les aires ? Rép : non.