Cours de mathématiques de 6e30. Triangles et quadrilatères |
|
VideoNote : dans cette leçon (à part dans l'introduction) on se limite aux quadrilatères dans le plan. |
Texte
Un triangle est une figure formée de trois sommets et des segments qui les joignent. Un triangle tient toujours dans un plan.
Un quadrilatère dans le plan est une figure formée de quatre sommets et des segments extérieurs qui les joignent. On appelle "côtés" les segments extérieurs, et "diagonales" les deux autres segments.
Faisons une sortie dans l'espace. Contrairement au triangle, un quadrilatère peut ne pas être dans un plan. Il peut être "tordu", comme un cadre en métal qui aurait été faussé.
Définition : un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
Note: : dans la suite de la leçon, on se limite aux quadrilatères dans le plan.
Propriété des parallélogrammes :
- Si un quadrilatère est un parallélogramme, alors il a un centre de symétrie.
- Si un quadrilatère a un centre de symétrie, alors c'est un parallélogramme.
Un peu de logique :
- Les parallélogrammes font donc partie de l'ensemble des quadrilatères qui ont un centre de symétrie.
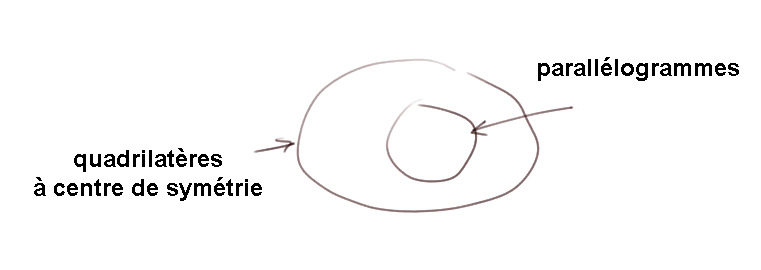
- Mais aussi, les quadrilatères à centre de symétrie font partie des parallélogrammes.
Donc les quadrilatères à centre de symétrie et les parallélogrammes (c'est-à-dire les quadrilatères à côtés opposés parallèles) forment une seule et même collection d'objets mathématiques. En d'autres termes, dans le plan un quadrilatère est un parallélogramme si et seulement si il a un centre de symétrie. (On en déduit par exemple que les côtés opposés d'un parallélogramme ont la même longueur, car la symétrie, qu'elle soit centrale ou axiale, préserve les longueurs.)
On ne "démontrera" pas la propriété en gras ci-dessus, se contentant de constater que géométriquement on la voit bien. La raison pour laquelle on ne la démontrera pas est que "démontrer", en mathématiques, veut dire "revenir à des résultats plus élémentaires déjà établis auparavant", et en déduire logiquement le résultat sur lequel on travaille. Et les résultats plus élémentaires découlent eux-mêmes de résultats encore plus élémentaires. A l'origine on a juste des "objets mathématiques fondamentaux" et des règles.
Le premier mathématicien à avoir traité la géométrie comme cela (objets et règles de base, puis déduction -> nouveaux résultats, puis encore déduction -> nouveaux résultats, etc.) est Euclide (325 avant J.-C, 265 avant J.-C.). Il est célèbre pour avoir vainement essayé de démontrer, avec ses principes de base et ses règles, que, dans un plan, si on a une droite D et un point P en dehors de la droite, il n'existe qu'une seule droite passant par P et parallèle à D. Finalement, il l'a rajouté comme principe de base. On l'appelle "le postulat d'Euclide".
Cette discipline des "démonstrations" à partir de principes ou résultats plus en amont n'est pas inintéressante. Elle est cependant un peu aride. Et en géométrie élémentaire, elle tend à créer plus de confusion qu'autre chose dans l'esprit des élèves, car on ne distingue pas toujours très bien ce qui a été démontré de ce qui est un principe de base. Quand nous irons plus loin en géométrie, nous démontrerons plus souvent des résultats.
Un peu de logique (suite). Considérons l'ensemble des êtres vivants :
- Si un être vivant est un homme, alors il est mortel*.
- Mais tous les êtres vivants mortels ne sont pas des hommes.
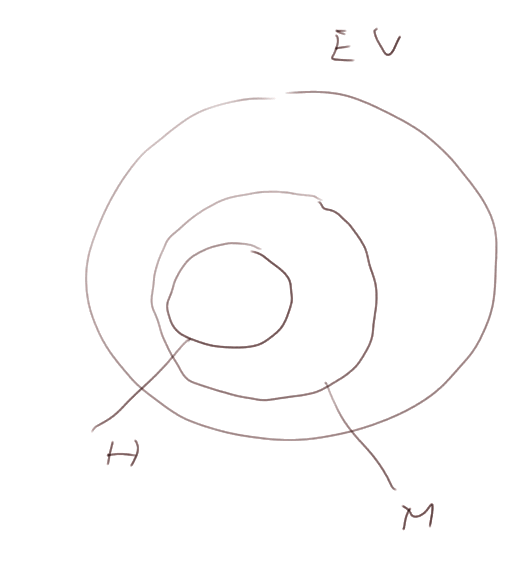
Là les deux sous-ensembles, Hommes et Mortels, des êtres vivants ne sont pas les mêmes : les hommes sont une partie, et seulement une partie, des êtres vivants mortels. Tandis que les parallélogrammes et les quadrilatères à centre de symétrie sont exactement la même sous collection des quadrilatères.
(* noter que les amibes ne sont pas mortelles.)
Aire des parallélogrammes : Aire = Longueur x hauteur.
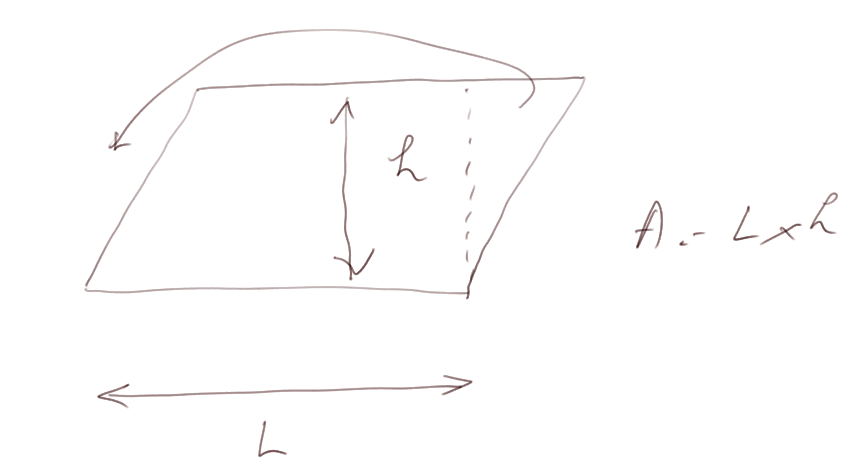
On le voit en déplaçant le triangle de droite vers la gauche, et revenant ainsi au cas du rectangle.
Aire des quadrilatères quelconques : il y a beaucoup de façons géométriques de calculer l'aire d'un quadrilatère quelconque, mais il n'y a pas de formule générale simple. En pratique, l'une des façons est de découper le quadrilatère en plusieurs triangles et on calcule les aires de chacun d'entre eux. (Une autre façon est présentée en exercice plus bas.)
Voyons un exemple où le quadrilatère est dessiné dans le plan avec un répère.
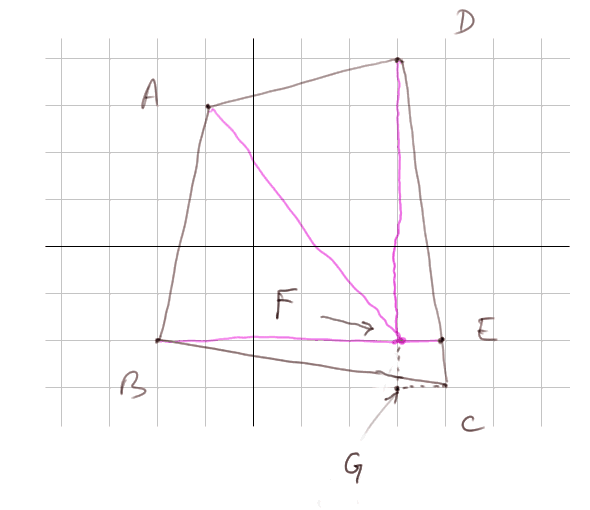
|
Le quadrilatère quelconque est ABCD. Pour calculer son aire on le découpe avec les deux droites BE et DF, et enfin avec AF. La seule difficulté est de connaître la longueur du segment BE, ou, ce qui revient au même, du segment FE.
FE = 6/7 cm. Pourquoi ? On verra ça précisément plus tard. Pour l'instant, observons que les droites horizontales du quadrillage découpent le triangle DGC en échelons de longueur dégressive régulièrement depuis GC (= 1 cm), jusqu'au point unique D (longueur de DD = 0). Le premier échelon intermédiaire, FE, fait 6/7, le deuxième 5/7, le troisième 4/7, etc. jusqu'à la pointe du triangle (le point D) qui fait 0/7.
Alors l'aire de DFE est 6 x 6/7 x 1/2 = 36/14
Aire de BEC = BE x hauteur x 1/2 = (5 + 6/7) x 1 x 1/2 = 41/14
Aire de ABF = 25/2 et aire de ADF = 24/2.
Donc l'aire du quadrilatère complet ABCD est 36/14 + 41/14 + 25/2 + 24/2. On ramène tout au dénominateur 14.
Aire de ABCD = 36/14 + 41/14 + 175/14 + 168/14 = (36 + 41 + 175 + 168) / 14 = 420/14 = 30 centimètres carrés (si l'unité du quadrillage est le centimètre).
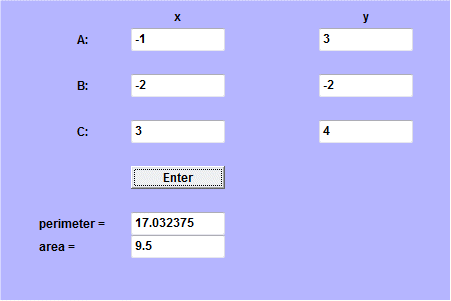
Le calcul peut être vérifié à l'aide de ce logiciel de calcul de l'aire d'un triangle. Par exemple, on calcule l'aire du triangle ABD en entrant les coordonnées des trois sommets (dans le logiciel les trois points s'appellent toujours A, B et C...).
Le logiciel calcule que ça fait 9,5.
De même l'aire de BCD fait 20,5.
Donc l'aire du quadrilatère ABCD est bien 30.
Calculer l'aire de ABFD en observant que le quadrilatère est inscrit dans un rectangle, aux côtés horizontaux et verticaux, et en calculant alors la surface du rectangle ainsi que la surface des éléments en dehors du quadrilatère.