FINANCIAL ANALYSIS

Financial Analysis

FINAL EXAMINATION with answers

2nd semester

Write your answers in the blank space below each question.

Question 1: Explain the difference between Accounting and Finance.

The main difference concerns the role of time. Accounting is a technique of recording transactions on an on-going basis. When a sale is paid with an IOU, the IOU is recorded at its face value, even though it corresponds to cash which will arrive at a future date.

In finance a promise, signed at time t, to pay a sum of money M at a future date T, has a value today (at time t) which is less than M. To calculate the present value of the promise, one must take into account external market conditions, the risk of the promise not to be paid, etc.

See course for more explanations.

Question 2: Suppose agent A is considering making an investment. The investment would be the purchase of an activity. If A does not buy the activity, the future cash flows of A will be

today	in 1 year	in 2 years	in 3 years	in 4 years	etc.

	50	60	70	80	etc.

And if the activity is not bought by A, it will have, as a standalone, the following cash flows:

etc.

(that is, the activity will have only two non zero future cash flows)

Suppose if A buys the activity, the future cash flows of A will become

etc.

(that is, in year 3 and after, the cash flows will be the same as without the purchase).

Would it be a physical investment or a financial investment? Explain.

We observe that the cash flows for A, in the case A buys the activity, will be higher than the sum of [the cash flows of A without the activity] + [the cash flows of the activity as a standalone].

We explained in class that this is the characteristic of physical investments. That is, there is a synergy between A and the purchased activity which creates extra cash flows for A, higher than those of the activity if it staid a standalone.

Question 3: Explain why in financial investments NPV is zero.

On the other hand, when the cash flows for [A + the activity] are simply the sum of [the cash flows of A without the activity] + [the cash flows of the activity as a standalone] we are talking of a financial investment.

In that case the seller to A of the activity will sell it at a price equal to [the present value of the future cash flows of the activity as a standalone,] therefore for A it will be a purchase with NPV = 0.

Question 4: A security S will have a unique expected cash flow in one year of 250€. Its price today is 185€.

If you buy it, what is your expected profitability?

(250 – 185) / 185 = 35,1%

Question 5: Consider this wheel of chance n°1

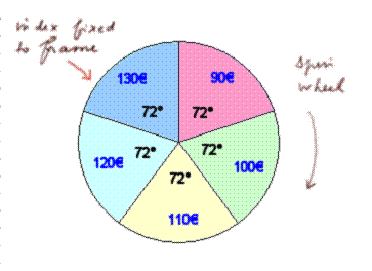
What is the expected payoff?

Each of the five sectors, paying a sum of money between 90€ and 130€, has the same probability 72°/360°, that is 1/5. So the calculation of the expected payoff is

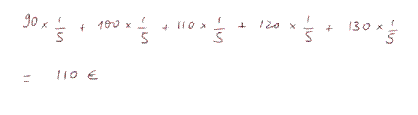
What is the standard deviation of the payoff?

If we call X the random payoff, the standard deviation of X is the square root of the variance of X. And the variance of X is given by the formula

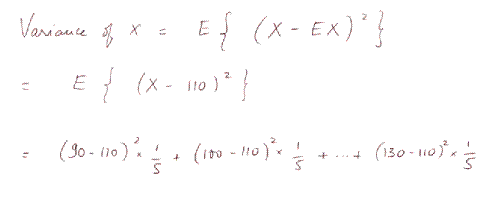
This yields var(X) = 200, and standard deviation of X = 14,1€

Question 6: Suppose you play the following game:

You pay 95€ to play
We spin the wheel n°1
You win the payoff which comes out

What is your expected profitability?

Our expected payoff is 110€.

So our expected profitability is (110 – 95) / 95 = 15,8%

Question 7: Consider the wheel of chance n°2

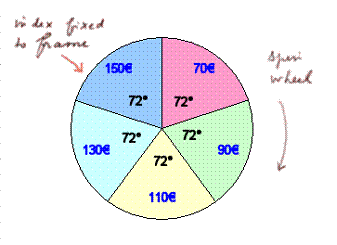
What is the expected payoff?

The payoffs have changed, but the probabilities are the same. The new calculation is

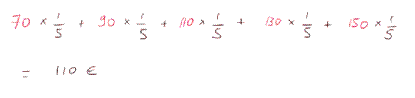
So as we see the mean hasn’t changed.

What is the standard deviation of the payoff?

The new variance is 800, and the new standard deviation 28,3€.

Question 8: Suppose the game with wheel n°2 also has an entry ticket of 95€. Between the two games, n°1 and n°2, what would an investor prefer? Explain.

The two games offer the same expected payoff, but with different risk.

As we explained in class, investors are risk averse (for reasons linked to the Saint-Petersburg paradox, explained in 1738 by Daniel Bernoulli), so they will prefer game n°1.

Question 9: Explain why a gambler would not necessarily have the same attitude as the investor.

The St Petersburg paradox explains that if you have a certain sum of money, say 1000€, in your pocket, in normal circumstances the utility of the last 50€ (that is, going from 950 to 1000) is a bit higher than the utility of an extra 50€ (that is, going from 1000 to 1050€).

For this reason, you’d normally prefer to have 1000€ for sure, than the result of a game where you’ll win 950€ with probability 50% and 1050€ with probability 50%.

But there are situations where the extra 50€, which you may win on top of the 1000€, have more utility than the other 50€ which you may lose from 1000€.

It is the situation of gamblers, which you see in gambling spots every morning scratching lotos, rapidos, and other astros. They prefer the situation where they will lose most certainly their 10€ of bets but may have the remote possibility of winning 1 000 000 € (yet their net expected gain is close to -10€), to just keeping their 10€.

Question 10: Consider the following investment (figures in millions of euros)

	year 0	year 1	year 2	year 3

cash flows	-100	50	50	50

What is the NPV if the opportunity cost of capital is 10%?

We have to compute the present value of each future cash flow C_n, using the formula

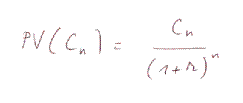
where r is the discounting rate (here 10%).

	year 0	year 1	year 2	year 3

cash flows	-100	50	50	50

present values	-100	45,45	41,32	37,57

sum	24,34
(including -100)

So the NPV is 24,34 million of euros.

Question 11: What is the IRR of the investment of question 10? (display your calculations)

One way to solve for the IRR is to try various discounting rates

For r = 10%, the NPV is 24,24

For r = 20%, the NPV is 5,32

For r = 30%, the NPV is -9,19

So the IRR is between 20% and 30%.

Some further trials and errors (or a linear interpolation) gives

IRR equals (approximately) 23,4%.

Question 12: Consider the following two investments (figures in millions of euros)

Investment 1	year 0	year 1	year 2	year 3

cash flows	-100	50	50	50

and

Investment 2	year 0	year 1	year 2	year 3

cash flows	-100	0	150	0

Compare them using two different methods of evaluation of investments.

With the payback period, investment 2 is the preferred one, because you get your money back faster.

But with the standard discounting method, computing the NPV, investment 1 is always the best (no matter which discounting rate you use) because the 50 gotten year 1 more than counterbalance the 50 gotten only year 3.