Review of CAPM

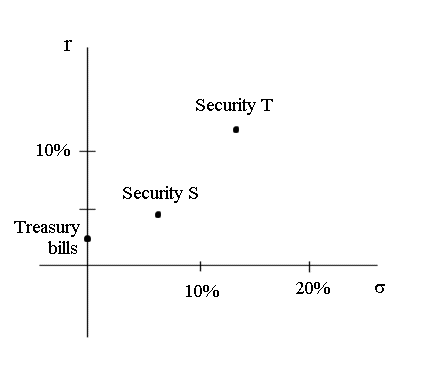
Risk return graph to position any security

• abscissa axis : s_S
• ordinate axis : r_S
  
  
• 

CAPM theory identifies, for any security, a fundamental risk and a specific risk (akin to an extra roulette wheel generated randomness)

• fundamental risk (= market risk, = undiversifiable risk, = systematic risk, = risk which cannot be eliminated) vs...
• ...specific risk (which can be eliminated by averaging out in a portfolio of "similar" securities).
• It is a mathematical result in linear algebra of RVs
• TB have zero risk, zero variability. Their return is the minimum (average) return one can get in the market. And it is sure.

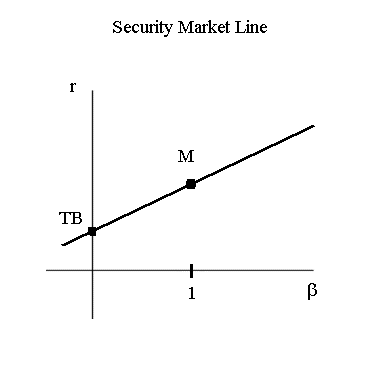
CAPM main results

• One central portfolio is the "market portfolio", denoted M
• M is well approximated by any well diversified portfolio of 20 to 40 securities (eg : S&P portfolio, DJ portfolio)
• Define, for any security S sold in the market, b_S = covariance(R_S, R_M) / Var(R_M)
• It is approximated by the slope of the straight line fitted, with the appropriate method, through a scattergram of past outcomes of (R_M, R_S)
• R_S = r_TB + b_S (R_M - r_TB) + e_S
• We say that S moves "like the market" with a "reactivity factor" b_S, plus an extra random term e_S the mean of which is zero.
• Let's look at the expectation of R_S (denoted r_S)
• r_S = r_TB + b_S (r_M - r_TB)
• Let's look at the variance of R_S (denoted s²_S)
• s²_S = b²_S * s²_M + Var(e_S)
• The part b²_S * s²_M is called the undiversifiable risk of the security S
• A portfolio made of a few securities is also, itself, a security
• A central idea of CAPM is to "average out" the diversifiable part of the risk of securities of same b by pooling them into portfolios
• Remember, if you throw one die, you will get a random result with mean 3,5 and std dev 1,7. If you throw several dice, the average result won't change but the std dev of the average result will be reduced.
• beta of any security S is estimated from past history of S and M, and published by agencies like Merrill Lynch.
•