Bachelor of Arts in European Management 2nd year students Your name

Bachelor of Arts in European Management
2nd year students

CORRECTION

Managerial Finance
Mid-term examination

24 November 2004

Twenty questions, each worth 5 points.

Question 1 : What is the yearly interest rate paid by risk free borrowers, for short-term borrowings, in Europe nowadays ?

Note that yesterday the Fed increased again its primary rate :

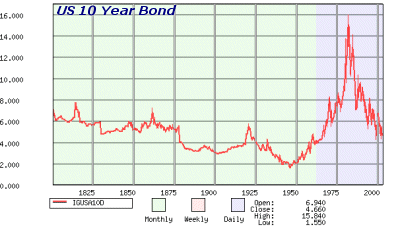
Fed nudges rates to 2.25% as trade gap widens to record $55bn (Guardian article)

Question 2 : What was the yearly interest rate paid in the United States, for the most typical borrowings (10 years), over most of the XIXth century (from 1800 to 1875 about) ?

Remember the following graph :

Question 3 : Describe, with a numerical example, two securities with the same profitability in one year, one with large risk and one with low risk.

Two ways to answer : consider two securities S and T (S will be high risk, T will be low risk, and both must show profitability say 20%. Suppose both have price 100 and expected value in one year 120)

1) illustration with two possible series of outcomes

S :
94 93 200 116 143 178 76

T :
125 120 115 123 124 131 117

2) illustration with the two densities of probabilities

S = LOI.NORMALE.INVERSE(E3;120;30)

T := LOI.NORMALE.INVERSE(E3;120;5)

Note that LOI.NORMALE.INVERSE(E3;4;1) is narrow in absolute value, but has the same risk pattern as S.

Question 4 : A random variable X has the following possible outcomes and probabilities :

Random variable X
a1 a2 a3 a4 a5
Outcome 90 120 150 190 250
Probability 15% 25% 30% 20% 10%

What is the expectation of X ?

The mean of X is by definition the weighted average of the possible outcomes, weighted with their probability.

(We saw that this is in accordance to experience, where if we “throw” the random variable many many times we will get proportion of each outcome according to its probability.)

E(X) = 90*15% + 120*25% +… + 250*10%

Once we accept the fact that some phenomena display a randomness WITH A LONG TERM STABILITY related to some physical symmetry, everything else (definitions and new concepts) is logical.

For instance : we know from experience that if we spin the wheel of chance (corresponding to X) many many times, we shall get the outcome 90 roughly 15% of the time.

This is really the gist of probability theory. In fact this relationship between the theory (E(X) …) and real life experience disturbed scientists until around 1930. In particular the idea that we cannot rule out highly unexpected outcomes.

Another disturbing fact is this : we saw that the probability to get an outcome of S in question 3 less than zero is very small. But this is true of any very narrow interval : the probability of getting an outcome between (87,5643253684 and 87,5643253685) is also very low. In fact we only talk about probabilities of intervals.

The guy who clarified it for good is Andrei Kolmogorov in 1931. He showed that probability models are only a branch of mathematics, a part of the theory of measure. Since then there is no more dispute.

90 120 150 190 250
15% 25% 30% 20% 10%

13,5 30 45 38 25

E(X) = 151,5

Question 5 : Give the formula to compute the variance of X

Var(X) = Expectation of { (X – E(X))2 }

A mathematical formula that cannot be read in plain English is a bad formula.

And if it can be read in plain English, then we can check whether it looks correct or not.

Compute the variance of X

(90 – 151,5)2*15% + (120 – 151,5)2*25% + … + (250 – 151,5)2*10%

Q5 567,3 248,1 0,675 296,5 970,2

Var (X) = 2083

Question 6 : What is the standard deviation of X ?

It is the square root of the variance. 45,6

Question 7 : Compute the mean and the standard deviation of Y

Random variable Y
a1 a2 a3 a4 a5
Outcome 90 120 150 190 250
Probability 10% 10% 60% 15% 5%

Q7 90 120 150 190 250
10% 10% 60% 15% 5%

9 12 90 28,5 12,5

E(Y) = 152

384,4 102,4 2,4 216,6 480,2 1186

St dev (Y) = 34,4

Explain heuristically the results you got for E(Y) and sd(Y) compared to those for X.

Y is more “packed” around its central values (where
necessarily the mean is, unless there were far outliers) than X

Therefore its standard deviation is smaller than that of X.

Question 8 : Suppose that the random variable X of question 4 is the future, unknown, payoff of a security S. If securities, traded on the market, and with the same risk pattern as S have an average profitability of 30%, how much should we pay today for S at the most ?

30% is called then the opportunity cost of capital of investing into S

And the price of S that the market will offer is

151,5 / (1 + 30% ) = 116,5

Here again we are at the heart of simple finance :
1. probability theory is only introduced because it is the best model we know of to work on future payoffs and current prices, etc. (There are other models, non probabilistic)
2. the above calculation of the price of S using its opportunity cost of capital is the accurate representation of the fact that investors prefer less risk for the same profitability. We saw that for any other price of S this rule is violated.

Heart of finance :

Computing the price we should offer for T :
What price should we offer for T ?
In order to solve this problem we have three important pieces of information :
1. The expected value of T in one year is 180€, with std dev 40€
2. T has the same risk pattern as a security S about which we know more things
3. The value of S in one year will be, on average, 6€ with a std dev of 1.333€ and S sells today for 5€. That is S yields an average profitability of 20%.
These are the three pieces of information, and only three pieces of information, we need to compute a price for T.

Considering that for Finance people the risk of a security is the standard deviation of its profitability (here the risk of S is 26.67%), and that for two securities with the same risk they will require the same profitability (fundamental fact of Finance, restated), we are in a position to compute the price of T.
There is a little twist in the argument that will follow, because we cannot talk about the risk of T until we have a price for it.
Claim : the price of T should be PT = E(Y) / (1 + rS)
This yields PT = 180 / (1 + 20%) = 150€

A higher price for T would violate the fundamental principle of Finance. But to verify this the argument is in two steps.
First, let's consider a higher price say PT = 160€ for T.
Under this hypothesis the security T for us has an expected profitability
E(RT) = [ E(Y) - 160 ] / 160 = 12,5%

A priori, why not ? If the risk is also less than the risk of S...
And indeed std dev (RT) = std dev { [ E(Y) - 160 ] / 160 } = std dev(Y) / 160 = 40/160 = 25%
So it looks like such a price for T is OK : "if we pay 160€ for T, we have less average profitability than with S, but we also have less risk..."

But it is not OK. Here is the final stab in the speculation "what about paying PT = 160€ for T ?" :
If indeed we don't like a risk as high as 26.67% (the risk of S), and are ready to give up some profitability to have a lower risk, we can still do better than T.
Let's take our 160€ ; let's spend 150€ buying 30 S's ; and we just spare the extra 10€ (we keep them in our pocket).
This is like "investing 160€ in a security V".
What is the expected profitability of V ? Ans. : 30/160 = 18.75%
What is the risk of V ? That is what is the std dev of the profitability of V ?
Ans. : std dev [ (30*X - 160)/160 ] = (30/160) * std dev(X) = (30/160)*1.333 = 25%

So, if we don't want to go higher than 25% in terms of risk, we don't need to go as low as 12.5% in terms of profitability. We can have a risk of 25%, with a profitability of 18.75%
Conclusion : paying a price of 160€ today for T violates the fundamental principle of Finance. Because there is a better security (V), in terms of profitability, with the same risk.

So the price we should pay for T is
PT = E(value of T in one year) / (1 + rS)

This is called "discounting the future cash flow of T by the discounting factor rS"

Question 9 : Suppose the random variable Y of question 7 is the future, unknown, payoff of a security T. Does T have the same risk pattern as S ?

Answer : It has the same expected value (approximately).
But : No, it doesn’t have the same risk pattern, it has a narrower risk pattern.

In which area should the price of T be ?

Since the value of T next year has the same expected value as that of S but has a narrower spread, investors will be willing to pay more for T than for S. (We assume, as always, that these variabilities come from systematic risk, not from unsystematic risk which is akin to artificially added variability with a random generating device.)

The price should be somewhere between the price of S and the max price for something yielding 152 in one year (which is 152 / (1 + 1,75%) = 149,4)

Ans : price of T will be somewhere between 116 and 149,4

Concerning unsystematic risk : according to the standard theory of finance (that we study in this course), if we consider a security V, with a price P_V today, and with a certain systematic variability in one year, if we add to the value of V in one year an extra random figure with mean zero, generated with a random device, we do not change the price of V today. Thus for instance, still according to the theory, a TB to the payment of which, in one year, we add artificially a random value with mean zero, does not see its price today decrease. That's one of the delicate aspects of the concept of opportunity cost of capital. But as long as we assume that we deal only with systematic risks we don't have to be concerned with this aspect. The CAPM explains in details how to get rid of unsystematic risk, which is akin to artificially added randomness with no real link with market conditions.

Question 10 : Give the definition of the concept of opportunity cost of capital of an investment.

The opportunity cost of capital of an investment is the profitability of a “good” security traded in the stock market and which has the same risk pattern.

This definition is important : it is a part of the model explaining and quantifying the attitude of investors in the stock market. It explains exactly the price investors will pay for one security.

Question 11 : Suppose we have had the possibility to realize the same investment many times (and the results are independent of each other). The actual yields we got are

-10,0
2,5
6,0
2,0
18,0
-1,0
2,5
-6,0
-5,5
14,0
3,5
0,5
5,0
7,5
4,0
-3,0
8,0
-4,5
10,0
9,5
-1,5
3,0
5,0
16,0
-3,0
5,5
0,5
1,5
6,0
-8,0
5,0
3,0
-5,5
0,5
-1,5
5,5
1,0
0,0
1,0
-7,0
6,0
4,0
0,5
0,2
-2,0
3,0
-3,0
7,0
0,0
4,5
-4,0
3,0
-3,5
2,0
10,0
4,0
6,0
4,0
2,5
1,0

Draw the histogram of these yields.

Done in class with the beginning of the same numbers.

To draw a histogram we need to select intervals for the values, and we count the values in each interval. We get a series of counts, their plot is the histogram.

Question 12 : What is the estimated mean and what is the estimated standard deviation of the profitability of this investment ?

Here two possible answers :

Either purely graphically from the histogram : fit a bell shape curve. Its middle is the estimated mean. The distance between the estimated mean and the “inflection point” (where the slope stops decreasing and begins to increase again) is the estimated sd

Or use arithmetics : mean of the 60 numbers = 2,25
Estimated sd : estimate the average squared deviation (sum up the 60 squared deviations and divide by 60 = 29,5) and take the square root = 5,43

Question 13 : Consider the following investment project (in millions of euros) :

Investment I
year0 year1 year2 year3 year4

CF -100 20 40 50 30

NPV

If the opportunity cost of capital to evaluate future cash flows today is r = 10%, what is the Net Present Value of this investment project ?

Apply the formula for DCF analysis.

Remember that justifying the formula requires some care. We need to prove that the formula represents correctly the behavior of investors in front of risk. Therefore we need to define how investors measure the risk in this investment and how they compare risks of several investments.

Q13 r = 10,0%

y0 y1 y2 y3 y4
1 2 3 4
CF -100 20 40 50 30

PV -100 18,18 33,06 37,57 20,49

NPV = 9,296

Question 14 : Let’s look at NPV of I as a function of r : What is the NPV(I ; 20%), that is, the NPV of I calculated with r = 20%.

Q13 r = 20,0%

y0 y1 y2 y3 y4
1 2 3 4
CF -100 20 40 50 30

PV -100 16,67 27,78 28,94 14,47

NPV = -12,2

Question 15 : What is the Internal Rate of Return of the project ? (Use a graphical estimation, or any other technique you like.)

From NPV(I ; 10%) = 9,3
And NPV(I ; 20%) = -12,2

By linear interpolation we figure out that it is zero around 14,3%

A linear interpolation is a technique where we assimilate (it is an approximation) a curve, over a small interval, to a straight line, and then we apply elementary high school geometry to make some computation. In fact we use a variety of Thales theorem (-600 bc in Milet)

A more exact calculation yields : 13,9%

(But students got full credit for 14,3% and the picture of the interpolation)

A blurb on numbers : introduction of negative numbers, usefulness (it solves the equation x + 1 = 0 ; I had a lent marble, I lost it, I gain a new marble, I’m somehow back to zero, therefore the number of marbles I had after having borrowed a marble and lost it satisfies x + 1 = 0 ), notation (XVIth century !), introduction of solutions to x² + 1 = 0

It is exactly the same extension : it does not serve to count apples in a basket, but it is useful for other things (for instance phenomena involving sinusoidal movements).

The implicit ideas contained in the names “real numbers” and “imaginary numbers” are STRONGLY MISLEADING, in fact they hamper theoretical progress (even outside the realm of mathematics).

Question 16 : In the Polyzone project
Polyzone project : revised US view 2
Discount rate = 8%
Production costs = 30
0 1 2 3 4 5 6 7 8 9 10
year 0 year 1 year 2 year 3 year 4 year 5 year 6 year 7 year 8 year 9 year 10

initial inv ($ millions) 100

production schedule 0 0 40 80 80 80 80 80 80 80 80
(million pounds)

Price / pound ($) 1,2 1,2 1,2 1,2 1,1 0,95 0,95 0,95 0,95 0,95 0,95
Revenues ($mio) 0 0 48 96 88 76 76 76 76 76 76
Production costs 0 0 30 30 30 30 30 30 30 30 30
Transport costs 0 0 4 8 8 8 8 8 8 8 8
Other costs 0 20 20 20 20 20 20 20 20 20 20

Cash flows -100 -20 -6 38 30 18 18 18 18 18 18

Present values = -100,00 -18,52 -5,14 30,17 22,05 12,25 11,34 10,50 9,72 9,00 8,34

NPV = -10,28

we saw that the revised view of the project by the US firm was no longer attractive.

Explain how they came to that conclusion :

They began with a DCF including a price (1,2 all along) that overlooked the fact that the European competition would be attracted and have no transportation cost. Therefore the European competition would drive the price down. And they had to review their DCF. It went from + 63 million dollars to -10 million dollars.

Question 17 : Compute a second revision of the NPV of the Polyzone project (for the US firm) if the US firm manages to reduce its production costs to $25 millions per year (beginning year2 as above).

Push the new DCF analysis calculations : result 18,6 million dollars.

Question 18 : For which value – roughly - of the yearly production costs does the NPV become zero ?

Using a linear interpolation reasoning (or estimation) we get : 28.

Question 19 : Study of the variability of an investment J.
Here is an investment J with two future cash flows. The table gives, as is usual, the expected cash flows C1=60 and C2=70.
Investment J
year0 year1 year2

CF -100 60 70

NPV

Suppose that the actual future cash flows have the following possible values and probabilities :
C1 can take the values 50, or 70 with probabilities ½ each.
C2 can take the values 60, or 80 with probabilities ½ each.

And they are independent, that is the four possible pairs of values have probabilities ¼ each.

The four possible values of the IRR of J are

C1 C2 IRR
case 1 50 60 6,4%
case 2 50 80 17,9%
case 3 70 60 20,0%
case 4 70 80 31,0%

What is the expected profitability of J ?

Idea of question 19 : to think about how to appreciate the risk of an investment.

Remember that the purpose of theoretical Finance is to construct an operational model of the behavior of investors. We saw that investors apply the following rule for simple securities : between two securities with the same expected value in one year they are willing to pay more for the one that has less variability in one year (that is the one with the smaller risk pattern sd(X)/E(X) ).

This lead us to a proof that the price for a security T is E(value of T in one year) / (1 + opportunity cost of T)

Then we have to model how investors choose between two multi-year cash flow investments. For that we introduced the notion of risk pattern of a multi-year cash flow investment, and opportunity cost of an investment, and we extended our model the standard way.

What is the risk of J ?

You have the choice of investing into J or investing into a security U (worth today 100) and which will have the following random value Z in one year

Random variable Z
a1 a2 a3 a4 a5
Outcome 111 115 118 125 130
Probability 15% 25% 30% 20% 10%

Show that U has the same profitability as J.

What would you prefer : to invest into J or to invest into U ?

U will be preferred by investors : same profitability, less risk.

Question 20 : What is the most destructive : burn a pile of bank notes or burn a plant ? (Explain)

Ans : burn a plant.

When we burn a plant we destroy for good a tool to produce wealth.

That is not the case when we burn banknotes. We only destroy our claim to some wealth, but whatever we could have bought with the banknotes is still here.

In fact in France when we destroyed some banknotes, if we saved the numbers on the notes we can go to the Banque de France and get some new ones.

Is inflation destructive ?

The above explanations notwithstanding, yes inflation is destructive. It disrupts social links. Savers lose the purchasing power of their savings, so they are mad, they begin to distrust democracy and contemplate voting for a demagogue (=A leader who obtains power by means of impassioned appeals to the emotions and prejudices of the populace)...