Example of kabbalistic notations in mathematics that are best avoided

Contents:

-- Construction of the projective plane
-- Usefulness
-- Remark
-- Example of application: Pappus' theorem

Construction of the projective plane

This "projective plane" which is a very important concept in geometry, and which the author of the book from which the image above is taken designates by 

ℝP² = { ℝ³ \ (0, 0, 0) } / ~   

is in fact built like this:

We place ourselves in ordinary three-dimensional space, and we consider on the one hand a given point, for example the origin, and on the other hand a plane that does not pass through the origin, for example the horizontal plane P defined by z=1.

We consider all the lines that pass through the origin. They form a beam radiating from (0, 0, 0). All the lines of the beam intersect the plane P, except those in the horizontal plane z=0.

We associate all the lines of the beam that intersect the plane P with their point of intersection with P. And we say that the other lines correspond to "points at infinity" that complete the plane P. We denote this completed plane by the sign P*.

Note that a direction in P* and that obtained by making a half-turn of 180° correspond to the same point at infinity.

The plane P plus its points at infinity, denoted therefore P*, is called projective plane.

Usefulness

With this astute construction, there is now a one-to-one correspondence between the lines of the beam and the points of the projective plane P*.

Why go through this construction, with a beam of lines radiating from the origin, to describe the projective plane P*? Answer: because now to each point of P* corresponds a line of the beam. But in the plane P* all the points do not have the same nature: some are "ordinary" others are "at infinity". While in the radiating beam, all the lines have the same nature.

Furthermore, in projective geometry, we are often led to operate a central projection of a plane onto another non-parallel one. Then points which are at infinity on one are generally no longer so on the other. So treating all points (ordinary or at infinity) in the same way is convenient. This is what the bijection between the points of P* and the lines of the line bundle from (0, 0, 0) achieves.

In other words, to reason on the geometry of P*, we can reason on the geometry of the line bundle in R³. And this often clarifies and simplifies things.

The lines of P* correspond to the planes in 3D space passing through (0, 0, 0). All planes intersect P in the usual way, the intersection being an ordinary straight line, except one plane -- the horizontal one -- which does not intersect P, but whose intersection with P* is the straight line at infinity of P*.

Now, for example, in P*, two straight lines always intersect. Either they are not parallel and have an ordinary intersection, or they are parallel and intersect at a point at infinity.

Remark

In our opinion   { ℝ³ \ (0, 0, 0) } / ~    is a "kabbalistic notation" that adds nothing and hides astute but elementary geometric notions.

In any case, an explanation will be required. The clearer and more geometric it is, the better.

Then the P* notation does the job perfectly.

You will never find a notation like   { ℝ³ \ (0, 0, 0) } / ~    in the work of Aleksandrov, Kolmogorov and Lavrent'ev. They present projective geometry in chapter III, section III.13, of volume 1. Their presentation is geometric and very simple. Then they show some non-intuitive, powerful and useful results of projective geometry. The intellectual energy of the reader is not requisitioned to advance painstakingly with a machete through banalities in kabbalistic notations, but is solicited to understand non-obvious things, useful and explained as simply as possible.

There is much worse in terms of hieroglyphic notations hiding obvious things -- or else brain-bending notions, but applying the principle of Jean Dutourd: "It is by his taste for useless exactitudes that we recognize the cretin."

Example of application : Pappus' theorem

Pappus was a Greek mathematician of the late Alexandrian school who lived in the 4th century AD. He is famous for having proved the following theorem: in a plane we consider two arbitrary straight lines (intersecting or parallel)

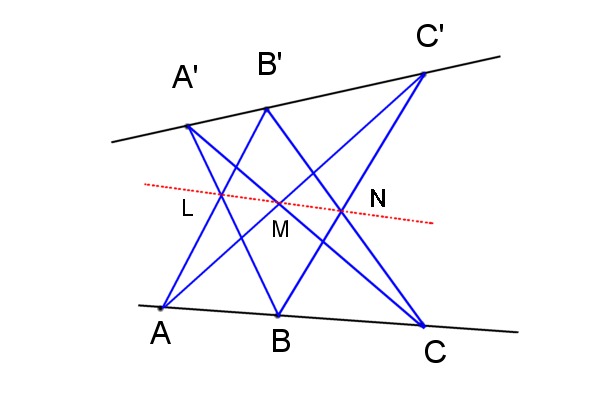
on the first we note three arbitray points A, B, C. And on the second three arbitrary points A', B', C'.

Then the points L, M, N, constructed as shown in the figure, are always aligned.

Pappus' theorem belongs to projective geometry. An important result, elementary to prove, is that if we have two projective planes P* and Q* and a point C outside them, then we can project all the points of the first onto the second, by drawing lines passing through C: this is called a central projection, and lines of P* remain lines of Q*.

Let's use this to prove Pappus' theorem (outline of the proof). We will now use the notion of length in a Euclidean space, which was not the case above, because projective geometry does not use the notion of length.

Let's project the line going through the points A', B', C' to infinity.

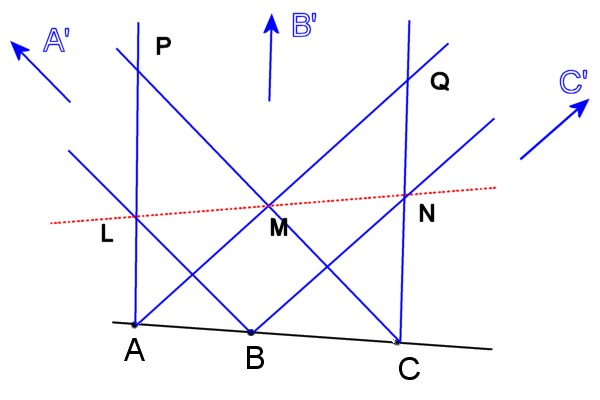
A' is projected to infinity, so lines BA' and CA' are now parallel. Same for the other two pairs.

Let's look at the figure above, and apply Thales' theorem:

Now the alignment of L, M and N is obvious, because by Thales we have PL/PA = CB/CA = CN/CQ.

Since in a projection of one plane onto another lines correspond only to lines, L, M and N were necessarily aligned in the first figure.