table des matières

 

Cours de mathématiques de 1ère S

Parabole inclinée : équation, paramétrage et dessin

Video

table des matières

introduction
repère canonique
paraboles à axe vertical
paraboles inclinées
changement de repère
équation de la parabole la plus simple inclinée à 45°
comment dessiner la parabole
paramétrage de la courbe
dessin à l'aide d'un tableur
problème pour aller plus loin
éléments de solution

 

Texte

Dans cette leçon, nous nous intéressons aux paraboles à axe vertical (les paraboles avec lesquelles on est familier) et aux paraboles à axe incliné (avec lesquelles on est peut-être moins familier).

Nous allons étudier plus spécialement la parabole inclinée la plus simple, passant par l'origine, et penchée à 45°.

 

On travaille dans le repère canonique habituel du plan, c'est-à-dire en langage de tous les jours une feuille quadrillée, avec les axes horizontal et vertical, et des petits carreaux par exemple de 1 cm de côté.

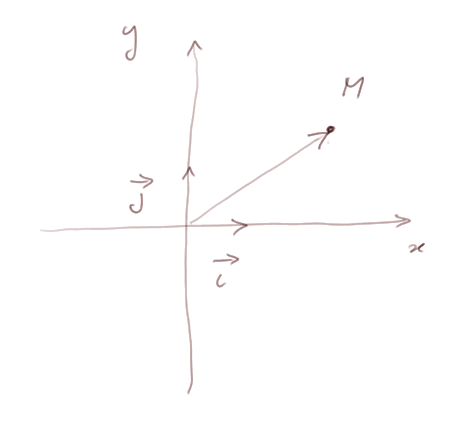
Dire d'un point M qu'il a pour coordonnées x et y dans ce repère, c'est équivalent à dire que

 

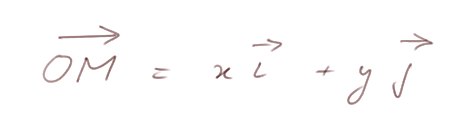
On est déjà familier avec les paraboles à axe vertical. Leur équation générale est y = ax2 + bx + c.

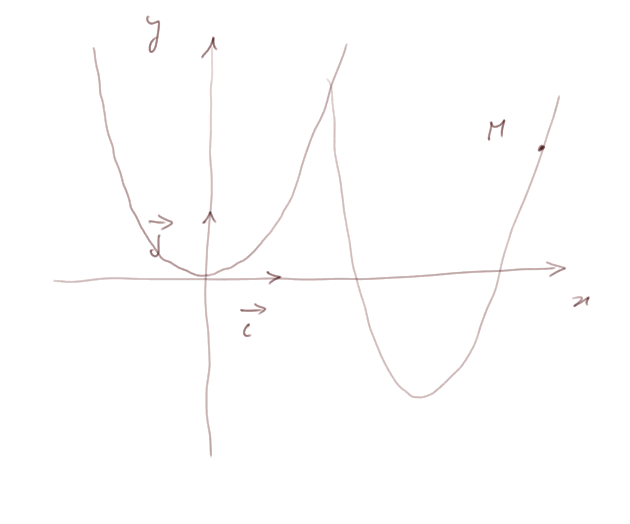
Voici l'utilisation de cette équation : Les points du plan, de coordonnées (x, y), tels que x et y satisfassent la contrainte y = ax2 + bx + c (où a, b et c sont des constantes données) forment un sous-ensemble - ou si l'on préfère, un lieu - du plan. Ce lieu est une parabole à axe vertical.

Si a est positif, la parabole s'ouvre vers le haut ; si a est négatif, elle s'ouvre vers le bas.

La parabole la plus simple, que l'on peut appeler "canonique", a pour équation y = x2.

Noter que l'équation (c'est-à-dire la contrainte)

y = ax2 + bx + c

se trouve aussi être l'expression d'une fonction de x. À chaque x sur la droite des réels, elle fait correspondre un y(x). Et l'ensemble des points [ x, y(x) ] est, encore une fois, une parabole à axe vertical.

En général l'équation définissant un lieu de points dans le plan n'est pas aussi l'expression d'une fonction.

 

Interessons-nous maintenant aux paraboles à axe incliné.

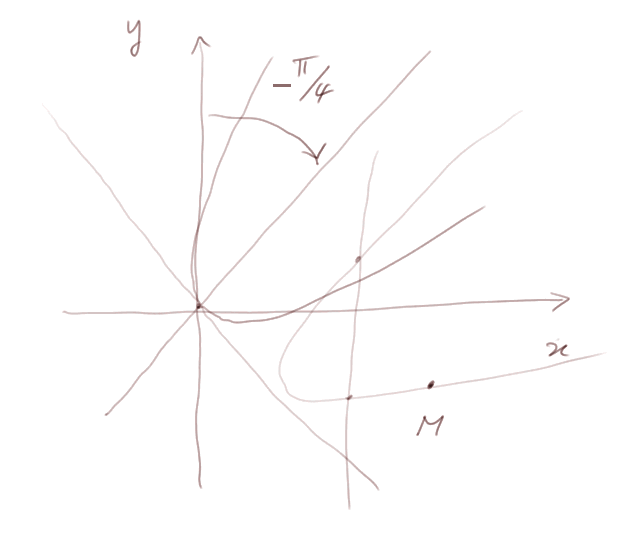
Le dessin en représente deux : une quelconque (celle avec le point M), et la parabole la plus simple qui a été inclinée à 45°.

On va chercher l'équation que doivent satisfaire les coordonnées d'un point M pour qu'il soit sur une parabole inclinée donnée. La forme générale de l'équation sera f(x, y) = 0.

Ce ne sera plus l'expression aussi d'une fonction y de x, car pour chaque x de la droite des réels, il y aura 0, 1 ou 2 points avec une certaine coordonnée y.

Restreignons le problème à la recherche de l'équation de la parabole "canonique" inclinée à 45° (c'est-à-dire celle qui avait pour équation, dans le repère i, j,

y = x2

est qui a été ensuite inclinée de -π/4.)

 

Pour parvenir à l'équation f(x, y) = 0, commençons par changer de repère.

On va travailler non seulement avec les vecteurs i et j, mais aussi avec les vecteurs u et v, qui ont chacun pour longueur 1 et qui pointent respectivement à -45° et à 45°.

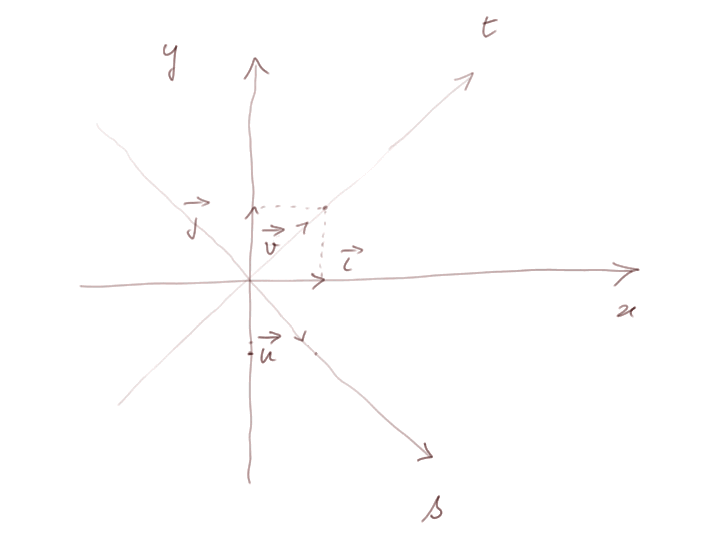
Les axes correspondant à u et v, nous les appelons l'axe des s et l'axe des t.

Dans ce repère, la parabole inclinée qui nous intéresse a de nouveau une équation très simple (en s et t). Mais procédons pas à pas. On va commencer par trouver les formules liant les coordonnées (x, y) d'un point M dans le repère (i, j) avec ses coordonnées (s, t) dans le repère (u, v).

On voit que i + j est un vecteur partant de l'origine et arrivant au sommet en haut à droite du carré formé par i et j. Donc il est égal à √2 fois v. De même i - j = √2 fois u. Avec les petites flèches au dessus, pour insister sur le fait qu'il s'agit de vecteurs, cela s'écrit :

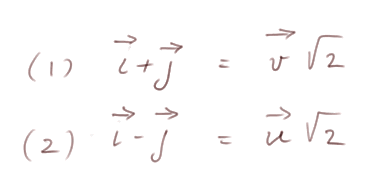
Comme on a vecteur OM = xi + yj = su + tv, en exprimant i et j en fonction de u et v, on va trouver s et t en fonction de x et y.

Additionnons les équations (1) et (2) ci-dessus. Cela élimine j et donne :

De même (1) - (2) élimine i et donne

d'où, après un peu de réorganisation,

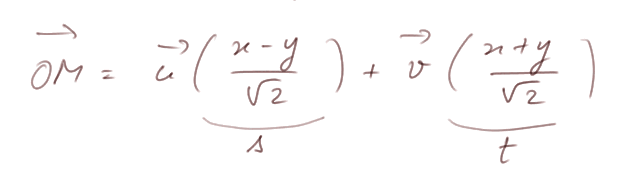
ce qui nous donne les formules de s et t en fonction de x et y.

 

Maintenant, nous pouvons écrire l'équation de la parabole que nous cherchons.

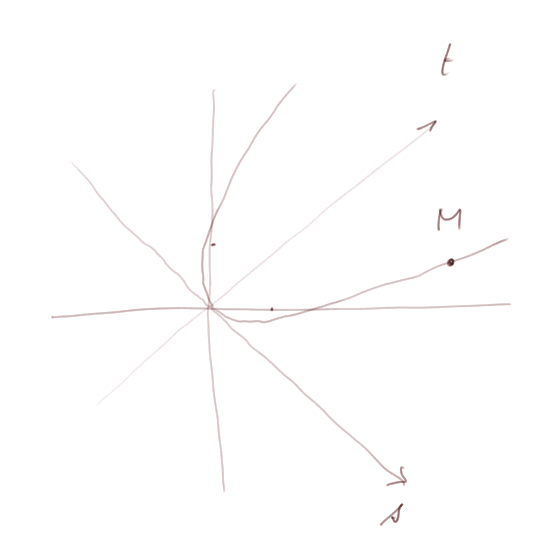
Dans le repère (u, v), c'est-à-dire dans le système d'axes s et t, elle a pour équation t = s2.

 

Comme on connaît l'expression de s et de t en fonction de x et y, on peut réécrire cette contrainte sur les coordonnées (s, t) de M, en une contrainte sur les coordonnées (x, y) du même point M.

L'équation t = s2 devient :

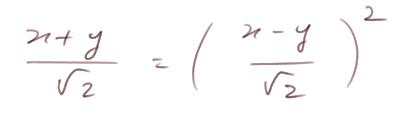
ou encore

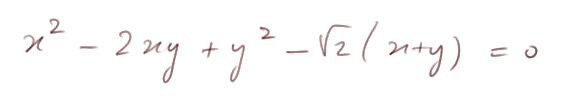
D'une manière générale une telle équation définit un lieu de points (= un sous-ensemble du plan), en l'occurrence la parabole inclinée à 45° vers la droite (c'est-à-dire inclinée de -π/4).

 

Abordons maintenant le problème du tracé de ce lieu de points à l'aide d'un logiciel courant.

Etant donné que la plupart des logiciels de dessin de courbes ne dessinent que des fonctions y = f(x), on se heurte à une difficulté. Car l'équation de notre parabole inclinée n'est pas l'expression d'une fonction. On ne peut pas la mettre sous la forme y = f(x).

Alors comment faire ?

 

Eh bien on va utiliser une idée simple et puissante : on va chercher à exprimer les coordonnées (x, y) de chaque point M de la parabole comme deux fonctions d'un paramètre. Quand le paramètre va varier le point M va se déplacer sur la parabole.

Il nous faut donc trouver une quantité p, liée à M, qui détermine de manière unique chaque point M.

 

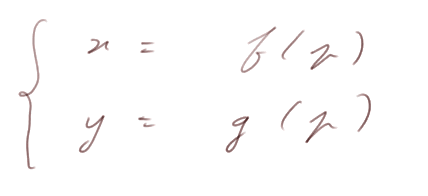
Quand on regardait des paraboles verticales, l'abscisse x faisait l'affaire : pour chaque x il y avait un point unique (x, y) sur la parabole y = ax2 + bx + c.

Mais x ne peut pas remplir ce rôle avec notre parabole inclinée, car pour certains x il y a 0 point M, pour d'autres il y en a deux.

 

Le paramètre : si on regarde bien notre parabole, on voit qu'il y a une quantité qui est en relation biunivoque avec les points M :

c'est la pente de la tangente à chaque point M.

Dans les axes (s, t), la pente de la tangente au point M est le nombre 2s, car la dérivée de la fonction t(s) = s2 est t'(s) = 2s. (Naturellement, on pourrait aussi prendre s lui-même, c'est-à-dire l'abscisse de M sur l'axe des s.)

 

Noter que ce paramètre ne conviendrait pas pour une ellipse, car à chaque pente de tangente correspondraient deux points.

Pour une ellipse il faudrait trouver un autre paramètre. On pourrait utiliser l'angle formé par le rayon allant de O vers M et l'axe des x, ou bien la longueur λ du segment d'ellipse montré sur la figure.

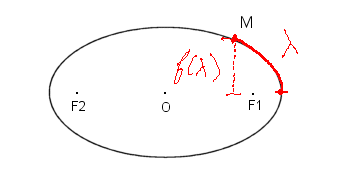
Dans ce dernier cas, l'ordonnée de M en fonction de λ est une fonction f(λ) dite "elliptique", qui a des propriétés très intéressantes. Elle a naturellement une période réelle égale à la longueur L de l'ellipse, c'est-à-dire que pour n'importe quel λ on a f(λ + L) = f(λ). Mais elle a aussi une période dans l'ensemble des nombres complexes qu'on étudiera l'année prochaine. Rappelez-vous qu'on connaît déjà des fonctions périodiques. Par exemple sinus, qui est justement la fonction f quand l'ellipse est un cercle, a pour période 2π, mais elle n'a pas de période complexe. La périodicité, réelle et complexe, joue un rôle très important dans de nombreux domaines des mathématiques plus avancées.

Mais revenons aux maths de 1ère S. Avec notre parabole inclinée, la pente est un excellent paramètre p.

Pour trouver les deux fonctions f et g telles que

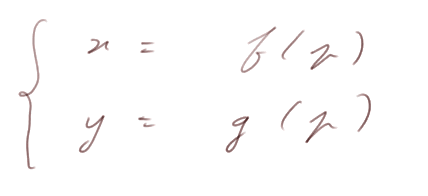
écrivons ce qu'on sait de p et s, t, x et y.

On a

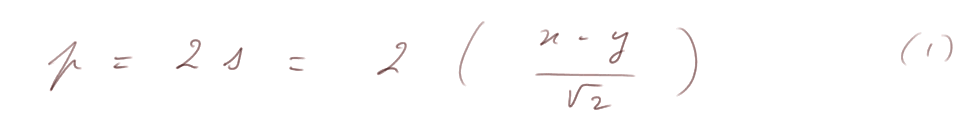
et

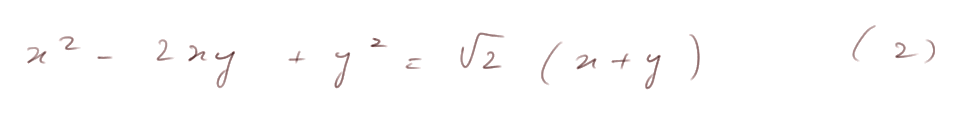
D'où l'on arrive au système

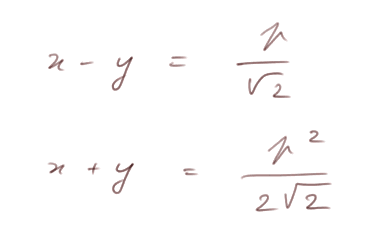
et finalement aux deux fonctions que l'on cherchait, exprimant les coordonnées x et y de M en fonction d'un paramètre p :

 

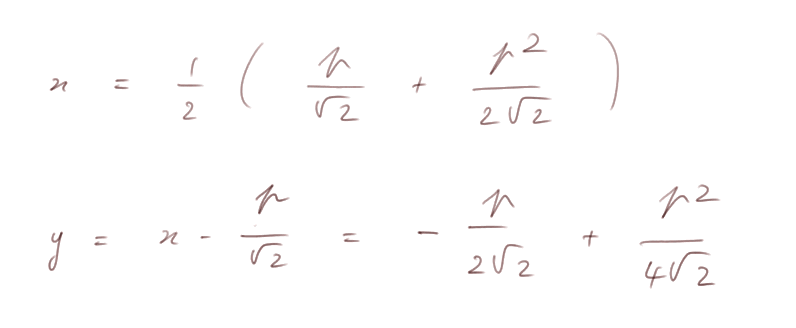
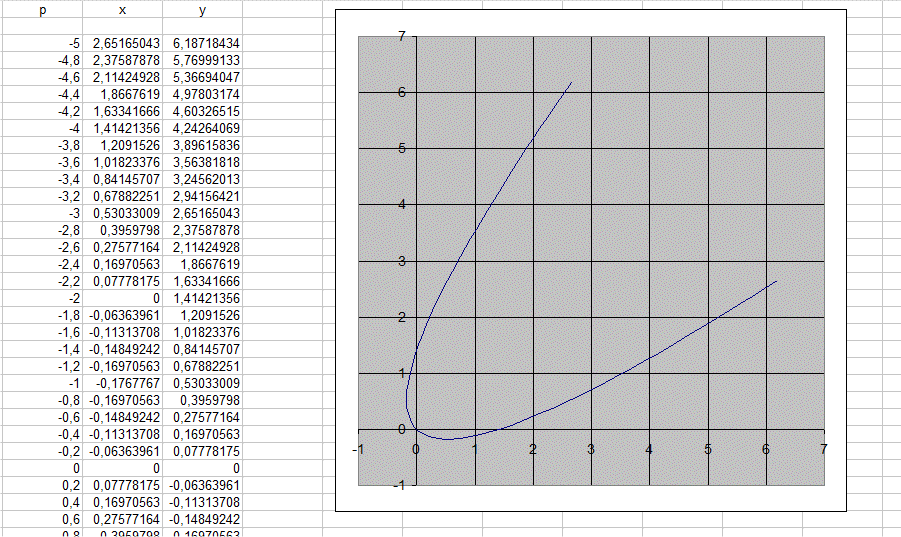
Utilisons un tableur pour dessiner une collection de points de la parabole :

 

 

Pour terminer, voici un problème pour aller plus loin. Soit les trois points A, B et C

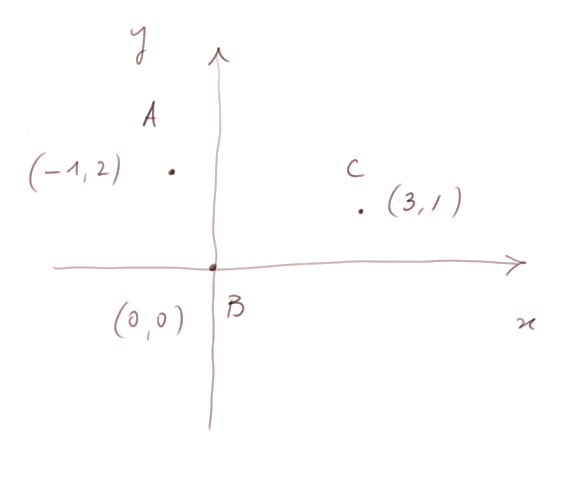
1) trouver les équations de toutes les paraboles qui passent par A, B et C

2) quel est le lieu de leurs foyers ?

Eléments de solution

Réponse

 

Les écrans de la vidéo




screen number
display zone

Plan général du cours

Contacter le professeur

 

 

Eléments de solution :

  1. Montrer que le foyer de la parabole y = x2 est (0, 1/4). Conseil :
    • Trouver la quantité d telle que chaque point de la parabole y = x2 est à égale distance du point (0, d) et de la droite y = -d.

  2. Montrer que le foyer de la parabole verticale quelconque [ y = ax2 + bx + c ] est

  3. Montrer que la parabole verticale passant par A (-1, 2), B (0, 0) et C (3, 1) est

    et que son foyer est ( 1,214...; 0,4315...)

  4. Si, dans le repère initial, M a les coordonnées (x, y), montrer que dans le nouveau repère incliné avec un angle θ comme ci-dessous

    M a les coordonnées (s, t) telles que


  5. Considérons dans le repère (s, t) la parabole verticale (c'est-à-dire d'axe parallèle à l'axe des t) d'équation générale t = αs2 + βs + γ. Imposons qu'elle passe par A, B et C dont les coordonnées dans (s, t) sont (sA, tA), (sB, tB) et (sC, tC). Montrer que (α, β, γ) doit être la solution du système d'équations suivant :


    qui peut aussi s'écrire, avec les notations matricielles, mais on n'en a pas besoin pour résoudre le problème


    ou encore T = Ψ E.

  6. Pour θ = π / 6 (c'est-à-dire 30°), montrer que les coordonnées de A, B et C dans le nouveau repère sont
     
    s
    t
    A 0,134 2,232
    B 0,000 0,000
    C 3,098 -0,634

    (important : vérifer avec un graphique sur papier quadrillé que ça a l'air exact)

    et, toujours dans le nouveau repère, que la parabole, parallèle à l'axe des t, a pour coefficients
    alpha -5,690
    bêta 17,423
    gamma 0,000

  7. Montrer que le foyer de cette parabole a les coordonnées suivantes :
    en (s, t) 1,531 13,293
    en (x,y) -5,321 12,278

    (continuer à vérifer avec un graphique sur papier quadrillé que ça a l'air exact)

  8. Pour un certain nombre de valeurs de θ entre 0 et π, faire les mêmes calculs et représenter, dans le système de coordonnées (x, y), le lieu des foyers obtenus. Conseils :
    • La connaissance du calcul matriciel permet d'aller plus vite, mais il n'est pas nécessaire pour résoudre le problème.
    • En notations matricielles, le système T = Ψ E de l'étape 5, a pour solution E = Ψ-1 T. Ce n'est rien d'autre que la formalisation avec les notations du calcul matriciel de la résolution générale d'un système de trois équations linéaires à 3 inconnues, que l'on sait déjà résoudre par exemple avec la technique du "pivot de Gauss".
    • Noter que le tableur Excel offre une fonction qui calcule l'inverse d'une matrice. Elle s'appelle =INVERSEMAT(ici, plage des coefs de la matrice initiale). Voir l'aide Excel pour son mode d'emploi.
    • Par exemple, quand θ = 0 comme dans l'étape 3, la matrice Ψ est
      1 -1 1
      0 0 1
      9 3 1

      Elle a pour inverse
      0,250 -0,333 0,083
      -0,750 0,667 0,083
      0,000 1,000 0,000


      Et le système E = Ψ-1 T donne
      alpha 0,583
      bêta -1,417
      gamma 0,000

      que l'on avait déjà trouvé quand on avait calculé que la parabole verticale (dans le système d'axes x et y) passant par les trois points A, B et C avait pour équation

 

Lieu des foyers :


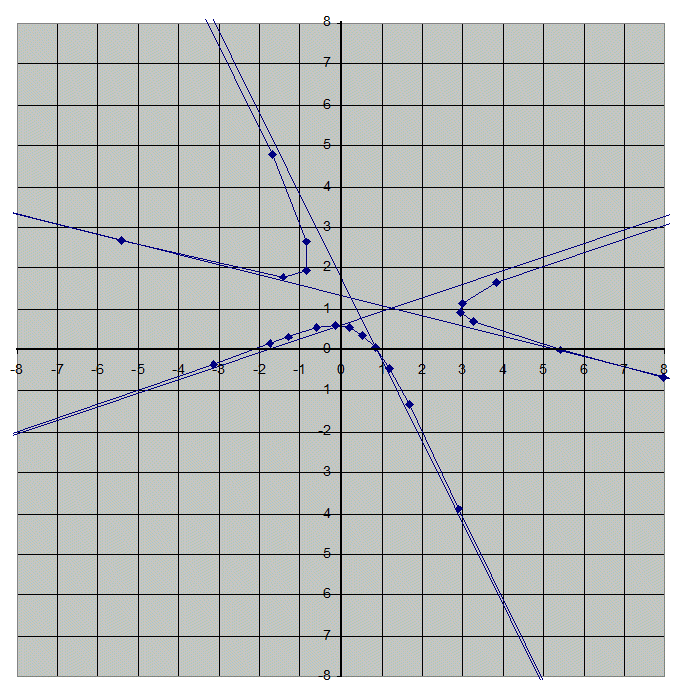
avec_triangle (tableur effectuant les calculs)

Noter que les trois asymptotes sont parallèles aux trois côtés du triangle ABC      .

 

" 'tain, si ça c'est facile...! " Θεόφιλος