Wednesday December 8th 2004
Finance : session 9 bonds part 1
What is a bond
Variations on simple bonds
Risk and randomness in bonds
What is a model
Bond market
Example of misleading and confusing explanations
Rates and risk
Quotation agencies
Bond rate structure
Basic calculations on bonds
The opportunity cost of capital of a
new bond
The NPV of a new bond is zero
A bond is a simple financial contract between a lender and a borrower :
at date 0 the lender accepts to lend money usually $1000 (for one bond) to the borrower, and the borrower promises to pay at the end of every year, for a certain number of years, a fixed coupon, and at the end of the final year he also promises to pay back the original $1000.
The lender (of money) is also called the buyer of the bond, and the borrower (of money) is also the issuer of the bond.
This is a contract for a series of transactions :
the initial lending is better viewed as a purchase of a bond by the lender from the borrower.
This is because the bond is a piece of paper with a value in the pocket of the lender, and this piece of paper can be resold, before the end of the contract, on the secondary market for bonds.
Here is a typical schedule of cash flows for one bond :
| Year0 | Year1 | Year2 | Year3 | Year4 | Year5 | Year6 | Year7 | |
| Future coupons | 80 | 80 | 80 | 80 | 80 | 80 | 80 | |
| Future final refund | 1000 | |||||||
| Initial purchase | -1000 |
This is a 7 year maturity bond, with a coupon of $80, which is often called an 8% coupon.
The above described bond is the simplest kind of bond. I will also call it : the standard bond.
Since a bond is a financial contract between two parties, markets invented many variations on the simple bond. For instance :
A simple bond can be viewed as the result of a negociation on the coupon value between the lender and the borrower : they agree first on the initial sum and final sum ($1000) as well as the maturity time (the number of years) and they negotiate the coupon value. Sometime the borrower fixes the coupon value, and ask for a bid price on the initial value. One may then see bonds like this :
| Year0 | Year1 | Year2 | Year3 | Year4 | Year5 | Year6 | Year7 | |
| Future coupons | 80 | 80 | 80 | 80 | 80 | 80 | 80 | |
| Future final refund | 1000 | |||||||
| Initial purchase | -950 |
The only thing to remember is that a bond is a private lending/borrowing contract with a schedule of repayments between an issuer (the borrower of money) and a buyer (the lender of money). So plenty of variations on the standard bond can be thought of.
The 80's and 90's saw a great deal of creativity and innovation in financial tools. That is why the subject of bonds, in particular, is so wide. But it is only due to refinements on the simple structure, and all the questions of evaluation they raise.
We shall meet later in this course a famous type of advanced financial tools (that have been around since the beginning of capitalism, not only in the past 20 years) to exchange value between two agents : options.
A call option is a contract between a buyer and a seller : at date 0 the buyer of the call option pays a certain sum, the price of the call option, to the seller ; and then at a given future date 1 the buyer has the right to purchase a certain security from the seller at a price specified at date 0.
A put option is a contract between a buyer and a seller : at date 0 the buyer of the put option pays a certain sum, the price of the put option, to the seller ; and then at a given future date 1 the buyer has the right to sell a certain security to the seller at a price specified at date 0.
As for bonds there are refinements : in European call options, the buyer can buy only at date 1 ; in the American call option, the buyer can buy at any time between date 0 and 1.
Calculating the price of an option (like we calculated the price of a security T from knowing its risk pattern and knowing the profitability of another security S with the same risk pattern) is the subject of Black and Scholes theory developed in the early 1970's.
A blurb on forwards and futures : an agreement today (date t) for an exchange at a future date (date T) of some assets for a price specified today (often denoted Ft,T). Example, in the spring (date t), a farmer and a cereal breakfast producer may agree on an exchange in the fall (date T, after the crop of corn) at a price specified today, in order to avoid the risk related to the day-to-day price of corn (called the "spot" price).
A blurb on hedging (example : buying stocks, and at the same time buying puts on the same stocks).
A blurb on the risk of derivatives. The collapses of Barings (1995), LTCM (1998), and Amaranth (2006)
A blurb on the reasons to issue bonds :
Risk and randomness in bonds :
The risk and randomness of a simple bond is not exactly the same as that of a security, although the same probability theory will be used of course (because there is only one).
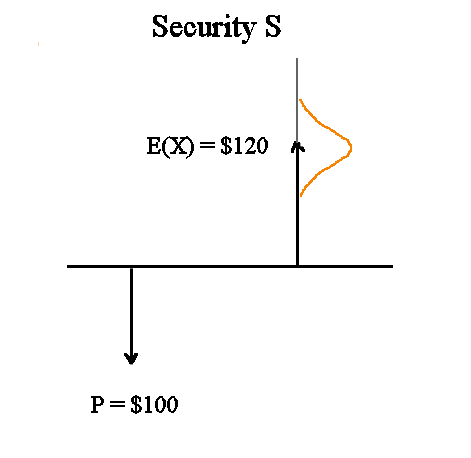
We saw that a security S has a future value in one year that is a random variable with a mean value and a spread :

We also saw this kind of randomness for an investment with cash flows over several years.
For simple bonds the situation is slightly different (but only slightly) : according to the contract the future cash flows are fixed, they are not random variables. There will be the stream of fixed coupons, and at the end year, together with the last coupon, there will be the final repayment of the face value.
In the universe of experiments with no economic problems there is no randomness here. (Remember : to talk about the probabilistic behavior of any measure we have to specify the universe of replicable experiments we take under consideration in our model.) In this universe, logically, lenders should accept the interest rate of risk free bonds : 1,75% in the US as at early December 2004. They don't. Why ?
They don't because this universe with no economic problem is not a good model of the economy of a country. Two things can go awry during the life of a bond :
In a more useful model to appreciate bonds, first of all the future coupons are random variables with two possible outcomes : the promised payment, and zero ; and secondly the "value of money" should be integrated one way or another.
The probabilistic modelling of the risk of defaulting is easy to achieve. We are back in the usual probabilistic model for securities and investments, except that we don't deal with random variables with bell shape frequency curves, and secondly they are not independant : if one coupon became zero, all the other payments are usually modeled as being zero too (or at least, their probability of being zero has increased tremendously : that is why there is a market for bad bonds at a big discount price from their normal trading value).
The modelling of change in purchasing power of money over time has not yet been done in an indisputably satisfactory way. The theory (and the fame) is still up for grab.
This section is a digression. It can be skipped in a first reading, to go directly to Bond markets.
Remember this idea : There is nothing complicated ; there are only things that can be confusing either because they are ill defined or because they are badly explained. However, things when they are new and innovative may require work from us to become familiar with them : there is much difference between being complicated and requiring practice. Finding one's way with a car in Paris is not complicated, but does require practice (taxi drivers with 20 years of experience are much better than new cabbies).
All phenomena we observe be they in Physics or in Finance are described, and worked on, with models.
Reading under the pen of a reputed accountant that "computing the unit price of a product in a multiproduct factory is complicated" is outrageous. It is not complicated, it is just artificial (if not meaningless) in the most standard (and perfectly instrumental) model of costs in a factory. The accountant believes that there is a true unit cost for a product, and that it is his job to get as close as possible to it. Such a common mistake points at two things :
Saint Thomas Aquinas, pursuing the ideas of Aristotle, said that in a good transaction the value received and the value given should be equal. This statement refers implicitely to the absolute value of objects, and also to "fairness" in exchange (an old judeo-christian idea).
But this model has proved very poor. We all know that in most exchanges both parties gain from their own viewpoint. (This is partially recognized in accounting with the notion of profit made on selling goods from stock.) And secondly all attempts at measuring an absolute value for an object have failed. (Usually it is tried via "the quantity of labor" contained in it.)
Finance theory is still full of paradoxes. Here is one : if I have in my pocket $1000 and I can invest them into a project with a positive NPV, then this project right now is worth more than $1000, and I can exchange right now my $1000 for more, by selling my project (this is actually done by young people with a good project who sell for cash a part of their project, to venture capitalists, while still on paper). One feels that Finance ought to explain this better.
Physics has been confronted with paradoxes in standard models several times in its history. A famous one lead, in 1905, to the extension of Newtonian relativity and eventually to the construction of the atomic bomb. Here is briefly explained the paradox : everybody is familiar with Newtonian relativity ; if I let this pen fall, it will fall vertically. Tomorrow, while in my car, and driving at constant speed (no more than 90 km/h of course :-) ), if I do the same experiment I will still see the pen fall vertically. This is called Newtonian relativity : "relative to my car, every dynamic phenomenon behaves just like in the fixed classroom". Now what about other phenomena, for instance phenomena involving light ? Since the XVIIth century we know how to measure the speed of light - not an easy feat ! But it was done observing carefully some astronomical phenomena.
Some natural questions then popped up in the minds of physicists in the second half of the XIXth century (following brillant work by Maxwell 1831-1879) : "What is the support of the movement of light ?", "Is it the same as for the waves formed in front of my boat when I throw a stone in the lake ?", "What is the speed of the Earth with respect to the "Ether" - the hypothetical equivalent to the water on which my boat floats and moves ?". They tried to answer these questions with plenty of sophisticated experiments, but always came up with the same disturbing fact : the speed of light is the same in all fixed or regularly moving environments, and there appears to be no way to substantiate Ether. They even wrote complicated equations to represent the "contraction of lengths" this entailed. But then, in 1905, a young scientist said : the reason for all these seemingly paradoxes is that there is absolutely no difference between experiments in the classroom and in the car moving at constant speed. It is not only dynamic phenomena that are the same, it's all Physics ! Whatever we observe in one referential, must be observed in the same manner in another "Galilean" one. This lead at the same time to a very simple derivation of the equations that scientists had already laboriously figured out. But it further lead to two dramatic consequences :
The young scientist of 1905 then extended is idea of relativity to phenomena happening near massive bodies (for instance the Earth) or in an elevator (the exension of the classroom and the moving car). It took him ten years to come up with general relativity, because the mathematics - tensor calculus -, and also other aspects of the model were intricate. After that he went back to another of his fields of interest : Quantum mechanics, that he had also touched upon in 1905, and he introduced fundamental randomness in the behavior of certain particles. And then he spent the rest of his life - another 30 years - trying to invalidate his own idea with extremely sophisticated experiments "obviously impossible". But these experiments were eventually actually achieved, some of the more famous ones in 1982 in Orsay, near Paris. Science is fun. The young scientist of 1905, Einstein 1879-1955, will be the subject of many celebrating books next year, an example of (simple) anticipation :-)
There are other examples in Physics, in Medicine and elsewhere of a change in models. Immunology is a particularly fascinating field in that respect : Nature has subtle ways to distinguish "me" and "not me", and repelling "not me" bodies, except in the case of reproduction, where "female me" produces "not me" and does not repel it. For the interested reader here are some further references : 1) the emergent self, 2) visual elements in Chinese poetry, 3) the labour theory of knowledge. They should only be the beginning of a personal reflexion.
Economics and Finance to a large extent have not yet accomplished their Copernician revolution. The ideas of absolute value and subsequent fair exchange are still present all over the place, and they hinder progress. (Reference : Nietzsche "Beyond good and evil".) A new model of value, credit, and money, that will be more instrumental, is called for. As usual at first it will be looked upon as a bag of tricks and ad hoc weird concepts, and then after a few years of practice it will become the standard description of reality.
Before we go back to simple calculations on simple bonds, keep in mind that many of the paradoxes you will encounter, and which will puzzle you, are not misunderstanding on your part (make sure, though, you have done all your homeworks before you think that you are in front of one of the paradoxes :-) ), but will be illustrations of the fact that the current model in Economics and Finance is not entirely satisfactory. This, like for any other discipline, has historical reasons. But there is no reason to think that it won't change.
The US bond market is bigger than the US stockmarket. The reason is because most of the trading of bonds is over the counter and is not recorded and published like the trading of stocks of listed companies. Secondly firms have few new issues of stocks, whereas they regularly issue new bonds, if anything to replace bonds that have been entirely refunded.
Here are some numerical figures (for what is recorded) :
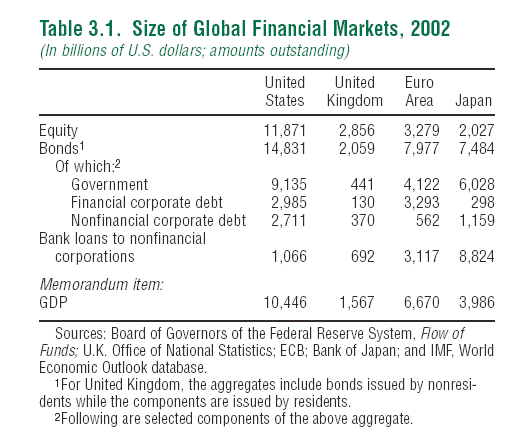
Source : http://www.imf.org/External/Pubs/FT/GFSR/2004/01/
"At more than $14 trillion in size, the U.S. bond markets are the largest securities market in the world. Turnover exceeds $500 billion daily and new issuances are expected to exceed $10 trillion this year. Despite the size, these markets operate without a central exchange, instead operating as an over the counter market with hundreds of market makers and thousands of participants."
Source : http://www.bondsonline.com/asp/us/us.asp
Example of misleading and confusing explanations :
Another source of information on bonds can be found on Yahoo site at http://bonds.yahoo.com/bond_ed.html
However, the explanations given on page 3 http://bonds.yahoo.com/sm_bd3.html are a good example of how to make bonds ununderstandable.
Here is a quote :
"Yield to maturity includes the fact that the bond you bought for $800 will pay you $1,000 when it's due. It also assumes you reinvest the coupons at the same rate and figures in the compounding effect. If, in the above example, you add that $200 difference and the effects of reinvested coupons, the yield to maturity calculates out to 7.73% -- a significantly better deal than the original coupon of 6%."
The "yield to maturity" that the page presents, as an arcane recipe of calculations, is simply the IRR of
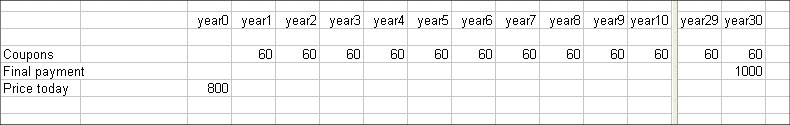
The IRR is 7,73%. Check it.
In other words, when for some reasons (that will be explained below in section 2) we can buy a bond with a discount from its face value we purchase something that will yield more than the coupon rate of the bond.
It is absolutely irrelevant whether we reinvest the intermediate coupons into purchasing more of this bond as its life elapses. In that respect the explanations on Yahoo are essentially wrong, quite misleading and confusing.
Unfortunately a large part of the literature on bonds and more generally on Finance, including respected textbooks, is of this flavor.
What determines the coupon rate of standard bonds ?
We saw it is the law of supply and demand between borrowers and lenders (in other word : negotiation), for bonds of certain quality.
What determines the quality of a bond ?
Answer : its risk in terms of the number of years our money will be blocked and in terms of the solvency (= the ability to meet maturing obligations as they come due) of the borrower.
Less solvent borrowers have to offer higher coupon rates, for the same maturity, than more solvent borrowers, in order to find money.
There are several agencies who make a business of evaluating and publishing quotations about the solvency of borrowers. The two most famous ones are Standard & Poor's and Moody.
Their best grade is AAA. Then AA, etc.
Treasury bonds of governments of rich countries are all graded AAA.
Bonds of large corporations are usually graded AAA, or in the next high grades.
When a borrower has a high grade from S&P or Moody, he will be able to borrow at comparatively low rates.
When a borrower is "downgraded" it is a big problem for him. His borrowings will become more costly, if not more difficult.
The present size (more than 1012 euros) of the French government debt (still graded AAA) is worrisome. It would not be surprising if, in the next 3 to 5 years, big agencies announced their intention to downgrade French TB.
This would be the beginning of serious financial and economic troubles in France, possibly social troubles, because the French government is the employer of many people and also has responsabilities in paying retirement pensions, as well as medical expenditures, etc. These are features of "the Welfare state".
And right now the French government meets all its obligations only through borrowing money to compensate the difference between its cash revenues and its cash outlays (no matter whether we count them as investments or as current expenditures). The order of magnitude of the debt increase from one year to the next, nowadays, is 50 to 100 billion euros. Here is the French budget deficit from 1950 to 2003 :
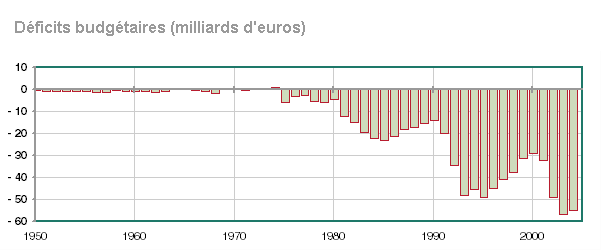
But this is only a part of the debt increase. There are other non totally funded expenditures outside the budget. More numbers here.
France is by and large not the only rich country faced with this problem.
A new bond coupon rate depends upon the maturity of the bond and upon the solvency of the borrower. In other words, it is a function of two variables.
For a given level of solvency of the borrower, the bond rate structure is usually an increasing relationship between maturities and rates.
Here is the structure of rates of US Treasury bonds as of December 9, 2004.
| Bond | Previous | Current | Change | % Change |
| 3 Month Bill | 2.24 | 2.23 | -0.01 | -0.45 |
| 6 Month Bill | 2.41 | 2.42 | 0.01 | 0.41 |
| 2 Year Note | 2.89 | 2.92 | 0.03 | 1.04 |
| 5 Year Note | 3.49 | 3.55 | 0.06 | 1.72 |
| 10 Year Note | 4.11 | 4.16 | 0.05 | 1.22 |
| 30 Year Bond | 4.78 | 4.83 | 0.05 | 1.05 |
| *Prices as of 12/9/2004 5:00 PM | Source: S&P Comstock |
Why is the yearly rate offered by the borrower (the US Treasury) for a 30 year borrowing higher than for a borrowing over a shorter period of time ?
Because if it were lower, instead of lending over 30 years, we (as a lender) would be better off lending our money for, say, 2 years, and at the end of the 2 years see whether we continue or not. We would lose nothing and we would gain the possibility of moving our money elsewhere after 2 years.
Put another way : in order to attract money into long term bonds the borrower must offer more attractive returns than for short term borrowings.
(There are odd situations where rates do not show this normal structure.)
More formally we can write : coupon rate of a new bond = function (solvency of the borrower, maturity of the bond)
r = f(s, n)
r is increasing when n increases, and is increasing when s decreases.
For the most solvent borrower (the US Treasury) the rate structure at the moment is this
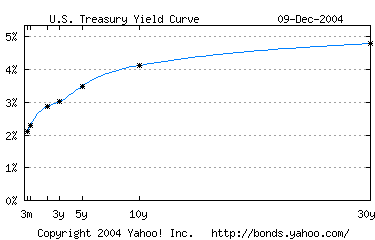
This is (simplifying life a bit) the curve of r = f(AAA, n) as a function of n (the maturity of the bond).
For less good borrowers (solvency = AA or less) the curves are shifted up. (See some numbers. You will see that real life is not as simple as theory : Municipal bonds at the moment appear to be safer than US Treasury bonds, whereas usually the ranking from safest down is : Treasury, Municipal, Corporations.)
A bond is a very simple mechanism to generate fixed profitability.
It extends over several years the simplest one year case. The one year case is this : we have $100 in our pocket, we invest them into a one year security, and we get after one year, say, $120 (on average, or fixed ; it does not matter for the argument). The profitability is 20%. With letter figures this becomes :
we invest today P into a security S and we get in one year CF1 = P*(1+rS)
Of course, as we saw, rS can be seen as the number r such that CF1/(1+r) = P
This simple fact extends to several year bonds.
Consider a bond B, with initial price $1000 (also called "the face value" for standard bonds), coupons of 8% of face value, and maturity n years.
Let us carry out a DCF analysis on the cash flows of the bond, using a discount rate r :
NPV(B, r) = -1000 + 80/(1+r) + 80/(1+r)2 + ... + 80/(1+r)n-1 + 1080/(1+r)n
Then this NPV will be equal to zero exactly when r = 8%.
Why ?
It is the extension of the case when n = 1.
Let's look at n = 2 and r = 8% :
NPV(B, r) = -1000 + 80/(1+r) + 1080/(1+r)2
Consider the last term : we have 1080 divided by (1+r) twice.
1080 divided by (1+r) once yields 1000. So we can rewrite, when r = 8%,
NPV(B, r) = -1000 + 80/(1+r) + 1000/(1+r)
Then, follow the reasoning once more :
80/(1+r) + 1000/(1+r) = 1000
So, when r = 8%, NPV(B, r) = -1000 + 80/(1+r) + 1080/(1+r)2 = 0.
In summary : a DCF analysis on a bond, carried out with its coupon rate yields NPV = 0.
Or more simply : the IRR of a new bond is its coupon rate.
The opportunity cost of capital of a new bond :
What is the opportunity cost of capital of a new bond ?
As for any security, it is the profitability of an optimal security with the same risk pattern, traded on the stock market.
This simple looking definition must be handled with care.
It is straightforward to handle only when we are considering the opportunity cost of another one year security, because in that case the risk pattern of the second security is simple to define.
In the case of a bond, as well as in the case of a multi-year-cash flows investment, the notion of risk pattern must be defined first, before we can talk about securities with similar risk pattern. (It is not particularly difficult ; it is done within a well specified probabilistic model ; the mathematics are a bit messier than for a one year security, unless we use particularly simple - in fact overly simplistic - probabilistic models.)
This is where being clear about the model, the concepts, and the definitions we use is fundamental (it is the reason of the above digression). Otherwise we become unclear, confusing, fuzzy.
We shall not prove it, because we shall not construct a complete probabilistic model to describe the risky behavior of the cash flows of a bond, but we shall assume (following intuition) that the opportunity cost of capital of a new bond is its coupon rate.
In other words, a new bond with coupon rate 10% has the same risk pattern as an optimal security with profitability 10%.
Remember that "proving it" amounts to no more than "choosing a good model" and then, within the model, pushing the arithmetics. We want to choose a model that represents well reality as we perceive it, but there is no absolutely correct model, it is up to us to a large extent. This is an interesting question in epistemology : to what extent our models follow reality, and to what extent our conception of reality follows our models ?
There are clear examples where people see only what their models show them. When we have a different and (we believe) more elaborate model than somebody else, we may be frustrated by this situation : the other person "sees" only what his interpretation of the world enables him to see. In that case, to convince the other person of our views, we must make predictions that he did not make and that he can check within his model. Sometimes it is impossible.
Therefore the NPV of a new bond is zero.
This is a consequence of the fact that the opportunity cost of capital of a new bond is its coupon rate.
By the way this is also one of the paradoxes of the simple model of Finance : the NPV of a bond being zero, Finance says that it is equivalent for the lender to either buy the bond, or to keep his money.
This is definitely not a totally satisfactory description of reality.