Les mathématiques et l'astronomie grecques à la fin de l'Antiquité

---------------------------------------------------------------------------------------

publicité

---------------------------------------------------------------------------------------

I.2.14 : LES MATHEMATIQUES ET L'ASTRONOMIE GRECQUES A LA FIN DE L'ANTIQUITE

Dans ce chapitre, nous nous intéressons aux mathématiques, pas en elles-mêmes, mais en relation avec la philosophie grecque -- une relation qui, particulièrement chez Platon, était étroite. La prééminence des Grecs apparaît plus clairement en mathématiques et en astronomie que dans quelque autre discipline. Ce qu'ils produisirent en art, en littérature et en philosophie, peut être jugé plus ou moins bon selon les goûts, mais ce qu'ils accomplirent en géométrie est indiscutablement remarquable. Ils apprirent des choses des Égyptiens, et dans une moindre mesure des Babyloniens ; mais ce qu'ils apprirent de ces sources était, en mathématiques, principalement des règles du pouce, et en astronomie des relevés d'observations sur de très longues périodes. L'art de la démonstration mathématique est, presque totalement, d'origine grecque.

Il y a de nombreuses histoires amusantes, qui n'ont probablement pas toutes une réalité historique, montrant quels problèmes pratiques stimulèrent les investigations mathématiques. La première et la plus simple se rapporte à Thalès, à qui, quand il était en Egypte, le roi demanda de trouver la hauteur d'une pyramide. Thalès attendit le moment de la journée où son ombre était aussi longue que lui était haut ; il mesura ensuite la longueur de l'ombre de la pyramide [en partant du centre de la pyramide sur le sol], et dit au roi que la hauteur de la pyramide était cette longueur.

On dit que les lois de la perspective ont été pour la première fois étudiées par le géomètre Agatharcos, afin de peindre des décors pour les pièces d'Eschyle.

Le problème de déterminer la distance d'un bateau que l'on voit au loin en mer, sur lequel Thalès dit-on se pencha, a été correctement résolu très tôt.

Duplication du cube, et irrationnels en général

L'un des grands problèmes qui occupa les géomètres grecs, celui de la duplication du cube, a pour origine, dit-on, les prêtres d'un certain temple, à qui un oracle avait dit que le dieu voulait une statue d'une taille double de celle qu'ils avaient [noter l'ambiguïté de l'expression "taille double" si on ne précise pas de quelle mesure on parle]. D'abord ils pensèrent simplement à doubler toutes les dimensions [linéaires] de la statue, mais ils se rendirent compte qu'ils produiraient une statue huit fois plus volumineuse que l'original, ce qui exigerait plus de dépense que ce que le dieu demandait. Alors ils envoyèrent une députation à Platon pour demander si quelqu'un à l'Académie pouvait résoudre le problème. Les géomètres s'attelèrent à la tâche, et y travaillèrent pendant des siècles, produisant, d'ailleurs, des travaux admirables. Le problème, bien sûr, est celui de déterminer la racine cubique de 2.

La racine carrée de 2, qui a été le premier irrationnel à être découvert, était connu des premiers Pythagoriciens, et d'ingénieuses méthodes pour trouver une valeur approximative furent mises au point. La meilleure était la suivante : formez deux colonnes de nombres, que l'on va appeler les "a" et les "b" ; chaque colonne démarre avec 1. Le "a" suivant à chaque étape est obtenu en additionnant les a et b de l'étape [ou ligne] précédente ; et le "b" est obtenu en additionnant 2 fois le "a" précédent au "b" précédent. Les six premières paires sont (1, 1), (2, 3), (5, 7), (12, 17), (29, 41), (70, 99). On montre aisément que le rapport b/a se rapproche de plus en plus de la racine carrée de 2. Par exemple le carré de 99/70 est, en notations modernes, 2,00020408...

Pythagore -- un personnage dont on sait peu de choses sûres -- est décrit par Proclus (+412, +485) comme le premier qui introduisit la géométrie dans l'éducation. De nombreuses autorités, dont Sir Thomas Heath dans son ouvrage "A History of Greek Mathematics", pensent qu'il découvrit lui-même le théorème qui porte son nom, c'est-à-dire : dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés. En tout cas, ce théorème était connu des Pythagoriciens à une date très ancienne [les dates de Pythagore sont -580, -495]. Ils savaient aussi que la somme des angles d'un triangle [dans un plan] était égale à deux angles droits.

Les irrationnels autres que la racine carrée de 2 furent étudiés. Théodore de Cyrène, un contemporain de Socrate, en étudia quelques-uns, et Théétète d'Athènes, qui était à peu près contemporain de Platon, juste un peu plus âgé, les étudia avec une approche plus générale.

Démocrite (-460, -370, donc une dizaine d'années plus jeune que Socrate, qui, lui, naquit vers -470, et mourut au terme de son procès en -399) écrivit un traité sur les irrationnels, mais on sait très peu de chose de son contenu.

[Démocrite pensait que les choses étaient faites d'atomes, mais aussi les figures géométriques, qu'à son époque on ne distinguait pas clairement des choses matérielles. Ainsi Démocrite pensait qu'un segment de droite était constitué d'une rangée d'atomes. A partir de là, le ratio des longueurs de deux segments était simplement le ratio de leur nombre d'atomes.

Par conséquent on peut penser que Démocrite rejetait les irrationnels comme ne pouvant pas correspondre à la réalité -- dans sa vision "atomique" des choses.

On ne sait pas ce qu'il a écrit sur le sujet. Mais la démonstration que la diagonale du carré est incommensurable avec le côté devait beaucoup le gêner, et le conduire à des raisonnements douteux pour rejeter ce résultat, comme ne s'appliquant pas à la réalité.]

Platon était profondément intéressé par le sujet ; il mentionne les travaux de Théodore et de Théétète dans le dialogue qui porte le nom de ce dernier. Dans Les Lois (819-820), il dit qu'une ignorance générale du sujet est quelque chose de disgracieux. On en déduit qu'il a lui-même un peu étudié les irrationnels, assez tard dans sa vie. Les irrationnels jouèrent un rôle comme on sait dans la philosophie pythagoricienne.

[Ils "montraient" une imperfection fondamentale dans la structure des nombres, auxquels les pythagoriciens avaient voulu attribuer une perfection absolue et qu'ils considéraient comme étant à la base de tout, musique, géométrie, toute chose dans l'univers en général.]

Théorie géométrique des proportions, et méthode d'exhaustion

Une des conséquences les plus importantes de la découverte des irrationnels fut l'invention de la théorie géométrique des proportions par Eudoxe de Cnide (c.-408, c.-355). Avant lui, il n'existait que la théorie arithmétique des proportions.

Selon cette théorie arithmétique (cf. "History of Greek Mathematics", Vol. I, p. 145), avec des notations modernes [inventées au XVIe siècle], le ratio de a/b est égal au ratio c/d si a x d = b x c. Cette définition, en l'absence d'une théorie arithmétique permettant de manipuler les irrationnels, n'est applicable qu'à des nombres entiers ou rationnels. Eudoxe, cependant, donna une nouvelle définition, géométrique, qui n'est pas handicapée par cette restriction. Elle est conçue d'une manière qui évoque l'analyse moderne. La théorie a été développée [ou plutôt surtout synthétisée et exposée] par Euclide et a une grande beauté logique.

Eudoxe a aussi inventé ou perfectionné la "méthode de l'exhaustion", qui fut par la suite utilisée avec grand succès par Archimède (-287, -212). Cette méthode anticipe le calcul intégral et différentiel. Prenez, par exemple, le problème du calcul de l'aire du cercle. Vous pouvez inscrire le cercle dans un hexagone régulier, ou un dodécagone régulier, ou un polygone régulier d'un millier ou un million de côtés. L'aire d'un tel polygone, quel que soit le nombre de ses côtés, est proportionnelle au carré du diamètre de cercle [Russell veut dire par là "dans une proportion fixe"]. Plus il a de côtés, plus près vous vous approchez de la surface [= aire] du cercle. On peut montrer qu'avec un polygone de suffisamment de côtés, son aire peut différer d'une quantité prédéterminée aussi petite qu'on veut de celle du cercle. Pour ce faire on utilise l' "axiome d'Archimède". (Dans une forme simplifiée) il énonce que si la plus grande de deux quantités est divisée par deux, et ensuite sa moitié est encore divisée par deux, et ainsi de suite, à une certaine étape on atteindra après une n-ième division une quantité plus petite que la deuxième. Avec des notations mathématiques élémentaires, si A est plus grand que B, alors il existe un nombre n tel que 2ⁿ x B est plus grand que A.

Pi et le cercle, circonférence et surface

[Pour terminer sur le calcul de l'aire du cercle -- que mystérieusement Russell délaisse pour faire plutôt des commentaires, voir ci-dessous --, en considérant les triangles qui forment le polygone, on voit que la surface du polygone est égale a une demi fois la distance du centre au milieu d'un côté quelconque multipliée par la circonférence du polygone. En passant à la limite comme Russell vient d'en faire le sketch, on arrive pour la surface du cercle * à

S = R x circonférence du cercle / 2

Par définition du nombre π, la circonférence L du cercle est

L = 2 π R.

Donc la surface du cercle est

S = π R²

Cela fait intervenir un autre irrationnel que racine de 2, ce deuxième irrationnel est π, qui dans une notation moderne est 3,14159... Contrairement à racine de 2, la démonstration que π ne peut pas être une fraction n'est pas évidente. Quant au fait que ce n'est même pas un nombre algébrique (racine d'une équation à paramètres entiers) cela n'a été démontré qu'à la fin du XIXe siècle par Lindemann.

* C'est d'ailleurs la définition en quelque sorte de la surface du cercle, car a priori les surfaces ne sont définies que pour des rectangles, et des triangles.]

La méthode de l'exhaustion parfois mène à un résultat exact [i.e. une proportion de nombres entiers], comme dans le calcul de la surface sous la parabole y = x² entre x = 0 et x = 1 [le résultat est 1/3]. Parfois, comme dans le cas de la surface du cercle, le calcul ne conduit qu'à une suite d'approximations sous formes de fractions de nombres entiers.

Le problème du calcul de la surface du cercle est le problème de la détermination de la circonférence du cercle en terme de son diamètre. Ce rapport est dénoté Pi [= π]. Archimède utilisait l'approximation 22/7 dans ses calculs ; en augmentant le nombre de côtés des polygones inscrits et circonscrits au cercle à 96, il démontra que Pi est plus petit que 3 + 1/7 et plus grand que 3 + 10/71. La méthode peut être employée à n'importe quel niveau d'approximation, et fait autant que n'importe quelle autre méthode dans ce problème. L'utilisation de polygones inscrits et circonscrits pour obtenir des approximations de Pi remonte à Antiphon, qui était un contemporain de Socrate.

Euclide

Euclide, dont l'ouvrage "Les Eléments" était encore dans ma jeunesse le seul manuel de géométrie reconnu pour les garçons, vécut à Alexandrie vers -300 [les dates conventionnelles d'Euclide sont c. -325, c. -250], quelques années après la mort d'Alexandre et d'Aristote. La plupart de ses Eléments ne sont pas originaux, mais l'organisation des propositions, et la structure logique, sont largement de lui. Plus l'on étude la géométrie, plus ces Eléments apparaissent admirables.

Le traitement des parallèles à l'aide du célèbre Postulat d'Euclide * sur les parallèles [qui dit que dans un plan où l'on a tracé une première droite et un point hors de la droite, par ce point ne passe qu'une seule droite parallèle à la première] a deux mérites : 1) il est rigoureux, et 2) il ne dissimule pas le caractère hypothétique du postulat. [De fait, au XIXe siècle János Bolyai (1802, 1860) et Nikolaï Lobatchevski (1792, 1856) développèrent des géométries avec d'autres postulats et elles s'avérèrent très importantes en relativité générale et dans d'autres domaines. Et elles sont ni plus ni moins cohérentes que la géométrie euclidienne, car dans la géométrie euclidienne on peut faire des modèles des autres, donc si les autres sont incohérentes, alors celle euclidienne aussi.]

[ * L'un des drames de l'enseignement par des professeurs de deuxième ordre c'est qu'au lieu de vous montrer la simplicité du raisonnement d'Euclide, et le caractère naturel du fait que son hypothèse sur les parallèles est un postulat, ils vous invitent à réfléchir sur la question de savoir si c'est vraiment un postulat ou bien si on pourrait le démontrer. Bref ils vous invitent à participer à la confusion qui régna autour de ce postulat de -300 à +1800 !

La même chose est vraie du paradoxe de Zénon d'Elée : j'ai connu des philosophes à la Sorbonne et ailleurs qui vous expliquaient que ce paradoxe était très profond, que la flèche ne pouvait pas atteindre Achille, etc.

J'ai aussi eu en 1969 au lycée Lakanal -- soi-disant un des bons lycées de la région parisienne dans les années 60 -- un prof de français en classe de 1ère (Monsieur Béchade) qui nous expliquait que les mathématiciens et physiciens déliraient quand ils disaient que l'univers pouvait être fini, au sens de 3-sphère, et qu'une ligne apparemment droite envoyée suffisamment loin dans une direction pouvait revenir dans la direction opposée.

A l'inverse Richard Feynman règle le problème de Zénon en deux phrases au début de son cours de physique. Mais Feynman était un grand esprit et un professeur hors pair ! ]

La théorie des proportions chez Euclide, à la suite des travaux d'Eudoxe, évite toutes les difficultés liées aux irrationnels [qui sont le fait que de nombreuses longueurs ne peuvent pas être exprimée comme des ratios de nombres entiers]. Elle le fait par des méthodes essentiellement similaires à celles introduites par Weierstrass (1815, 1897) en analyse au XIXe siècle [la rigueur des techniques analytiques ayant été déjà bien développée par Cauchy (1789, 1857)].

Euclide passe ensuite à une sorte l'algèbre de la géométrie, et traite, dans le Livre X, du sujet des irrationnels. Puis il enchaîne avec la "géométrie solide" [= géométrie dans l'espace à trois dimensions]. Il termine avec la construction des polyèdres réguliers, qui avait déjà été perfectionnée par Théétète et auquel il est fait mention [implicitement ?] dans le Timée.

Les Eléments d'Euclide sont certainement l'un des plus grands livres jamais écrits, et l'un des monuments les plus parfaits dédié à l'intellect grec. Ils sont bien sûr certaines des limitations typiques des Grecs : la méthode employée est purement déductive, et il n'y aucun moyen, dans le cadre de l'ouvrage, de tester les hypothèses ou axiomes initiaux. Ces axiomes étaient supposés être au-delà de toute question ; cependant, au XIXe siècle, la géométrie non-euclidienne montra qu'ils pouvaient être en partie erronés [allons bon, voilà que Russell retombe dans le Réalisme naïf !!!], et que seule l'observation pouvait décider s'ils étaient vrais ou pas.

Il y a chez Euclide un mépris affiché pour toute utilité pratique, qui avait été inculquée par Platon. On raconte qu'un écolier, après avoir entendu une démonstration, demanda ce qu'il gagnerait en apprenant la géométrie. Alors Euclide appela un esclave et dit : "Donne trois pennies à ce jeune homme, puisqu'il doit tirer un gain de ce qu'il apprend." Le mépris pour la pratique était, cependant, justifié pragmatiquement. Personne, à l'époque des Grecs, ne supposait que les sections coniques [ellipses, paraboles, hyperboles...] pouvaient avoir la moindre utilité ; enfin, au XVIIe siècle, Galilée découvrit que les projectiles se déplaçaient sur des trajectoires paraboliques, et Kepler découvrit que les planètes suivent des orbites elliptiques. Soudainement le travail que les Grecs avaient fait par pur amour du savoir et de la théorie devint la clé pour l'art militaire et l'astronomie.

Les Romains

Les Romains avaient l'esprit trop pratique pour apprécier Euclide ; le premier d'entre eux à le mentionner est Cicéron, à l'époque duquel il n'existait sans doute pas de traduction des Eléments en latin ; en effet il n'y a aucune mention d'une traduction d'Euclide en latin avant Boèce (c. +480). Les Arabes montrèrent plus d'appréciation : un exemplaire [en grec] fut offert au calife par l'empereur byzantin vers 760 ad [= +760], et une traduction en arabe fut réalisée sous Haroun al Rashid vers 800 ad. La plus ancienne traduction en latin d'Euclide qui nous soit parvenue a été faite à partir de l'arabe par Adelard de Bath (1080, 1152) en 1120. Après cela, l'étude de la géométrie redémarra progressivement en Occident ; mais ce n'est pas avant la Renaissance qu'eurent lieu de nouvelles avancées.

Astronomie

J'arrive maintenant à l'astronomie, où les réussites grecques sont aussi remarquables qu'en géométrie. Avant leur temps, parmi les Babyloniens et les Egyptiens, de nombreux siècles d'observations avaient posé des fondations. Les mouvements apparents des planètes avaient été notés, mais on ne savait pas que l'étoile du matin [Vénus, j'imagine] était la même que l'étoile du soir. Un cycle avait été découvert dans les éclipses, certainement en Babylonie et vraisemblablement en Egypte, qui rendait la prédiction des éclipses de lune relativement fiable, mais pas celles de soleil, car elles ne concernent pas toute la terre en même temps mais seulement une bande de position variable.

Nous devons aux Babyloniens la division de l'angle droit en quatre-vingt-dix degrés, et le degré en soixante minutes d'angle ; ils aimaient bien le nombre soixante, et construisirent même un système de numération où il joue un rôle important.

Les Grecs aimaient attribuer la sagesse de leurs premiers philosophes ou scientifiques à leurs voyages en Egypte, mais ce qui avait réellement été développé avant les Grecs se réduit à peu de chose. La prédiction d'une éclipse par Thalès est, cependant, un exemple d'influence étrangère ; il n'y a pas de raison de supposer qu'il ajouta quoi que ce soit à ce qu'il apprit de sources égyptiennes ou babyloniennes, et c'était un coup de chance que sa prévision d'une éclipse de soleil s'avéra vérifiable par des gens qui connaissaient Thalès.

Considérations sur la terre dans l'univers

Commençons par quelques-unes des découvertes et hypothèses correctes les plus anciennes. Anaximandre pensait que la terre flottait librement et n'était soutenue par rien. Aristote (De Caelo, 295b), qui souvent rejetait les meilleures hypothèses de son temps, avait des objections contre la théorie d'Anaximandre, lequel expliquait que la terre, étant au centre de l'univers, y restait immobile, car elle n'avait pas de raison d'aller dans une direction plutôt qu'une autre. Si cette théorie d'Anaximandre était valide, rétorquait Aristote, un homme au centre d'un cercle de nourriture placée régulièrement sur la circonférence mourrait de faim car il n'aurait pas de raison d'aller dans une direction plutôt qu'une autre. Cet argument réapparaît dans la philosophie scolastique, non pas en relation avec l'astronomie, mais en relation avec le libre-arbitre. Il réapparaît sous la forme du paradoxe de "l'âne de Buridan", qui était incapable de choisir entre de seaux d'avoine placés à égale distance de sa tête l'un à sa droite, l'autre à sa gauche, et qui par conséquent est mort de faim.

Pythagore, selon toute probabilité, est le premier à avoir pensé que la terre était sphérique, mais ses raisons étaient (on peut supposer) plus esthétiques que scientifiques. Des raisons scientifiques furent, cependant, rapidement offertes. Anaxagore découvrit que la lune n'émettait pas de la lumière propre mais réfléchissait la lumière qu'elle recevait, et il proposa une théorie correcte des éclipses. Il pensait encore, néanmoins, que la terre était plate ; mais la forme de l'ombre de la terre sur la lune durant les éclipses de lune apporta des arguments définitifs en faveur de sa forme sphérique.

Les Grecs savaient -- de Pythagore lui-même, dit-on -- que l'étoile du matin et l'étoile du soir étaient identiques, et ils pensaient que toutes les planètes, y compris la terre, se déplaçaient sur des cercles, non pas autour du soleil, mais autour d'un "feu central". Ils avaient découvert que la lune montre toujours sa même face à la terre, et ils pensaient que la terre montre toujours la même face au "feu central". Les régions méditerranéennes étaient du côté tourné vers le feu central, qui était par conséquent toujours invisible. Le feu central était appelé "la maison de Zeus", ou "la Mère des dieux". Le soleil était supposé briller grâce à la lumière provenant du feu central qu'il réfléchissait.

Le modèle pythagoricien où la terre n'est pas au centre de l'univers

A côté de la terre, il y avait un autre corps, l'anti-terre, à la même distance du feu central. Pour expliquer cela, ils avaient deux raisons, l'une scientifique, l'autre dérivée de leur mysticisme arithmétique. La raison scientifique était l'observation correcte qu'une éclipse de lune parfois survient quand à la fois le soleil et la lune sont au-dessus de l'horizon. La réfraction, qui est la cause de ce phénomène, leur était inconnue, et ils pensaient que dans ces cas-là l'éclipse était due à l'ombre d'un corps autre que la terre. L'autre raison était que le soleil et la lune, les cinq planètes, la terre et la contre-terre, et le feu central, faisaient dix corps célestes, et dix était le nombre mystique des Pythagoriciens.

Cette théorie pythagoricienne est attribuée à Philolaos de Crotone (-470, -390), qui vécut à la fin du Ve siècle avant J.-C. et fuit Crotone quand la population commença à s'opposer à l'école de Pythagore, et mourut à Thèbes. Bien qu'elle soit fantasmagorique et en partie tout à fait non-scientifique, elle est très importante car elle contient déjà une grande partie de l'effort d'imagination nécessaire pour concevoir, plus tard, l'hypothèse copernicienne. Concevoir la terre, non au centre de l'univers, mais comme une parmi les planètes, pas éternellement fixe, mais errant dans l'espace, montrait une extraordinaire émancipation par rapport à la pensée anthropocentrique. Une fois que la secousse initiale donnée à l'image que se faisaient les hommes de l'univers, il n'était plus très difficile de se laisser conduire par des arguments scientifiques vers une théorie plus correcte.

Inclinaison de l'écliptique (qui explique les saisons)

A cela diverses observations contribuèrent. Oenopide de Chios, qui vient un peu après Anaxagore, découvrit l'inclinaison de l'écliptique. Il devint bientôt clair que le soleil devait être beaucoup plus grand que la terre -- un fait qui allait dans le sens de ceux qui déniaient à la terre la position au centre de l'univers. Le feu central ainsi que la contre-terre furent abandonnés par les Pythagoriciens peu après l'époque de Platon. Héraclide de Pontus (c. -388, c. -315, un contemporain d'Aristote) découvrit que Vénus et Mercure tournaient autour du soleil, et adopta la vue selon laquelle la terre tourne sur elle-même en 24 heures. Ce dernier fut un pas très important, qu'aucun de ses prédécesseurs n'avaient fait. Héraclide était de l'école de Platon, et a dû être un grand homme, mais ne bénéficia pas d'autant de respect qu'il aurait mérité ; il est décrit comme un gros dandy.

Aristarque de Samos, le Copernic de l'Antiquité

Aristarque de Samos, qui vécut approximativement entre -310 et -230, et était donc environ 23 ans plus âgé qu'Archimède, est le plus intéressant de tous les anciens astronomes, car il proposa dès le IIIe siècle avant J.-C. l'hypothèse copernicienne complète, selon laquelle toutes les planètes, y compris la terre, tournent autour du soleil, et que la terre tourne en outre autour de son axe en 24 heures. Il est un peu décevant de trouver que le seul travail d'Aristarque qui nous soit parvenu, "Sur les tailles et distances du soleil et de la lune", adhère à la vue géocentrique. Il est vrai que, pour les problèmes que traite ce livre d'Aristarque, cela ne fait aucune différence quelle théorie est adoptée, et il a peut-être pensé qu'il était judicieux de ne pas alourdir ses calculs avec une opposition non nécessaire à l'opinion générale des astronomes ; ou il est peut-être parvenu à l'hypothèse copernicienne après avoir écrit ce livre.

Sir Thomas Heath, dans son livre sur Aristarque ("Aristarque de Samos, l'ancien Copernic", par Sir Thomas Heath, Oxford, 1913, tout ce qui est dit ici est basé sur son livre), qui contient le texte en grec d'Aristarque avec une traduction, penche pour la deuxième explication. L'évidence qu'Aristarque suggéra le modèle copernicien est en tout cas tout à fait convaincante.

La meilleure évidence vient d'Archimède (-287, -212), qui, nous l'avons vu, était un contemporain un peu plus jeune d'Aristarque. Ecrivant à Gélon, roi de Syracuse, il dit qu'Aristarque a publié "un livre consistant en certaines hypothèses", et il continue en disant : "Ses hypothèses sont que les étoiles fixes et le soleil ne bougent pas, que la terre tourne autour du soleil en suivant la circonférence d'un cercle, le soleil étant au centre."

Il y a aussi l'évidence suivante : dans un passage Plutarque dit que Cléanthe "pensait qu'il était du devoir des Grecs de condamner Aristarque de Samos pour impiété car il disait que la Terre de l'Univers (i.e. la terre) était en mouvement ; c'était la conséquence de sa tentative d'expliquer le phénomène [les jours, les saisons, etc.] en supposant que les cieux restaient immobiles et la terre tournait sur un cercle oblique, tout en tournant en même temps sur elle-même". Cléanthe était un contemporain d'Aristarque, et mourut vers -232.

Dans un autre passage, Plutarque dit qu'Aristarque avança cette vue seulement comme une hypothèse, mais que son successeur, Séleucos, la maintint comme une opinion définitive. (Séleucos vécut aux environs de -150.) Aëtius et Sextus Empiricus affirment aussi qu'Aristarque avança le modèle héliocentrique, mais ne disent pas qu'il le présenta seulement comme une hypothèse.

Qu'Aristarque pensât à son modèle héliocentrique seulement comme à une hypothèse ou comme à la réalité sûre, il est de toute façon vraisemblable, comme Galilée deux mille ans plus tard, qu'il fut influencé par la crainte d'offenser les préjugés religieux, une crainte que l'attitude de Cléanthe (mentionné plus haut) montre comme étant tout à fait justifiée.

Hipparque

Le modèle copernicien, après avoir été avancé, que ce soit comme une certitude ou comme une hypothèse, par Aristarque, fut définitivement adopté par Séleucos, mais par aucun autre astronome ancien. Ce rejet général était principalement dû à Hipparque, qui était actif entre -160 et -125. Il est décrit par Heath comme "le plus grand astronome de l'Antiquité" (Greek Mathematics, Vol. II, p. 253).

C'est le premier à avoir écrit systématiquement sur la trigonométrie ; il découvrit la précession des équinoxes (équivalent au mouvement de l'axe d'une toupie pour toute la terre) ; il estima la longueur du mois lunaire avec une erreur de moins d'une seconde ; il améliora les estimations d'Aristarque des tailles et distances du soleil et de la lune ; il établit un catalogue de 850 étoiles fixes, donnant leur latitude et longitude. En ce qui concerne son opposition à l'hypothèse héliocentrique d'Aristarque, il adopta et améliora la théorie de épicycles qui avait été inventée par Apollonius, qui vécut aux environs de -220 ; c'est un développement de cette théorie qui devint connu, plus tard, sous le nom de système ptolémaïque, d'après l'astronome Claude Ptolémée, qui vécut au milieu du deuxième siècle après J.-C.

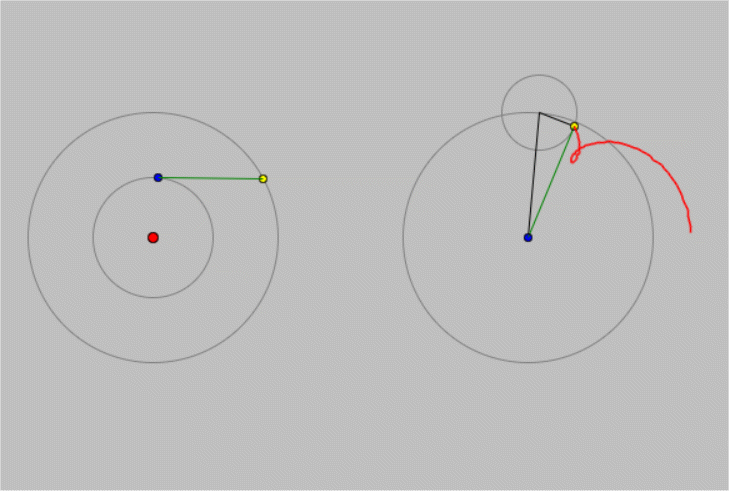
Système des épicycles de Claude Ptolémée pour expliquer le mouvement apparent un peu étrange des planètes vues depuis la terre (source : site du professeur J. J. Rousseau, université du Mans, cliquer sur l'image ou le lien pour voir une animation pédagogique)

Copernic (1473-1543) entendit parler, mais pas beaucoup, de l'hypothèse bien oubliée d'Aristarque, et fut encouragé par le fait qu'un Ancien ait eu la même idée que lui. A part cela l'effet de l'hypothèse d'Aristarque sur l'astronomie après lui fut pratiquement nul.

[Copernic lui-même prit soin que sa théorie héliocentrique fût publiée après sa mort naturelle.]

Taille et distance des corps célestes

Les astronomes anciens, pour estimer les tailles de la terre, la lune et le soleil, et les distances de la lune et du soleil, utilisèrent des méthodes qui dans leurs principes étaient valables [essentiellement de la trigo], mais furent handicapés par le manque d'instruments de précision.

Considérant ce manque, beaucoup de leurs résultats sont étonnamment bons. Eratosthène (-276, -194) estima le diamètre de la terre à 12630 kilomètres, ce qui est vrai à une centaine de kilomètres près ! Le diamètre moyen entre le diamètre à l'équateur et la distance entre les pôle est en réalité de 12742 km, avec une différence de 43 km [on sait que la terre à cause de la force centrifuge causée par sa rotation sur elle-même est une sphère très légèrement aplatie aux pôles].

Ptolémée estima la distance moyenne à la lune comme 29 ½ le diamètre de la terre ; le chiffre correct est 30,7.

Aucun n'arriva à une estimation raisonnable de la taille ou de la distance du soleil, que tous sous-estimèrent. Leurs estimations de la distance de la terre au soleil avec comme unité le diamètre terrestre sont :

Aristarque, 180

Hipparque, 1245

Posidonius, 6545

Le chiffre correct est 11 726. On observe que les estimations s'améliorent régulièrement (celle de Ptolémée non citée marquait cependant un retour en arrière). Posidonius, qui était le professeur de Cicéron, vécut dans la deuxième moitié du IIe siècle avant J.-C. Son estimation est la moitié du bon chiffre [ce qui commence à être une mesure respectable].

Globalement parlant, leur modèle du système solaire [si l'on retient celui d'Aristarque et non celui d'Hipparque et Ptolémée] n'était pas loin de la vérité.

Géométrie vs dynamique

L'astronomie grecque était géométrique, pas dynamique. Les Anciens pensaient que les mouvements des corps célestes étaient uniformes et circulaires, ou résultant de combinaisons circulaires [comme dans le modèle ptolémaïque avec des épicycles]. Ils n'avaient pas de concept de force. Il y avait des sphères complètes qui bougeaient rigidement, et sur lesquelles divers corps célestes étaient fixés. Avec Newton et la gravitation newtonienne un nouveau point de vue, moins géométrique, fut introduit. Il est curieux d'observer qu'il y a maintenant [depuis 1915] un retour vers le point de vue géométrique dans la Théorie de la Relativité générale d'Einstein, dans lequel le concept de force, dans le sens newtonien, est à nouveau banni.

Conclusion : le génie scientifique grec, et son extinction par les Romains

Le problème pour l'astronome est le suivant : étant donné les mouvements apparents des corps célestes sur la voûte céleste [qui est en deux dimensions, par exemple angulaires : longitude et latitude], introduire, par hypothèse, une troisième coordonnée, la profondeur [et chercher aussi le meilleur point à partir duquel mesurer cette profondeur], de telle sorte que la description des phénomènes deviennent aussi simple que possible.

Le mérite de l'hypothèse copernicienne n'est pas la vérité, mais la simplicité ; étant donné la relativité des mouvements [il n'y a aucun point fixe absolu, aucun repère, pas d'éther dans l'univers], aucune question de vérité ne se pose.

Les Grecs, dans leur recherche d'hypothèses qui "sauveraient le phénomène" [i.e. conduiraient à des conséquences cohérentes avec les observations -- c'est l'approche scientifique moderne], abordaient dans les faits, quoique pas totalement dans les intentions, le problème d'une manière scientifique correcte. Une comparaison avec leurs prédécesseurs, et avec leurs successeurs jusqu'à Copernic, convaincra n'importe quel étudiant de leur vraiment étonnant génie.

Deux très grands hommes, Archimède et Apollonius de Perga, au IIIe siècle avant J.-C., complètent la liste des mathématiciens grecs de premier ordre. Archimède était un ami, probablement un cousin, du roi de Syracuse, et fut tué [par un soldat romain] lors de la prise de la ville par les Romains en -212. Apollonius, dès son enfance, vécut à Alexandrie. Archimède n'était pas seulement un mathématicien, mais aussi un physicien qui étudia en particulier l'hydrostatique. Apollonius est principalement connu pour son travail sur les sections coniques. Je n'en dirai pas davantage sur eux, car ils vinrent trop tard pour avoir une influence sur la philosophie.

Après ces deux hommes, bien que des travaux encore respectables furent fait à Alexandrie, la grande époque des mathématiques grecques était révolue. [Russell oublie, entre autres, Héron d'Alexandrie, 1er siècle après JC, et Diophante d'Alexandrie, quelque part entre le 1er et le IVe siècle après JC] Sous la domination romaine, les Grecs perdirent la confiance en eux-mêmes qui va de pair avec la liberté politique ; et en la perdant ils acquirent un respect paralysant pour leurs prédécesseurs. Le soldat romain qui tua Archimède est un symbole de la mort de la pensée originale que causa Rome dans tout le monde hellénique.