Connaissance et perception chez Platon

---------------------------------------------------------------------------------------

publicité

---------------------------------------------------------------------------------------

I.2.8 : CONNAISSANCE ET PERCEPTION CHEZ PLATON

La plupart des gens considèrent comme indiscutable que la connaissance empirique dépend, ou découle, de la perception. On trouve cependant chez Platon et dans d'autres écoles de pensée une doctrine très différente, selon laquelle rien qui mérite le nom de "connaissance" ne peut être dérivé des sens, et la vraie connaissance concerne les concepts. De ce point de vue, "2 + 2 = 4" est une authentique connaissance, mais l'affirmation "la neige est blanche" est tellement remplie d'ambiguïté et d'incertitude qu'elle n'a pas sa place dans le corpus de vérités d'un philosophe.

Cette vue remonte sans doute à Parménide, mais dans sa forme explicite le monde philosophique la doit à Platon. Je me propose, dans ce chapitre, de traiter de la critique par Platon de l'idée selon laquelle la connaissance est la même chose que la perception. Cette critique occupe la première moitié du Théétète.

Ce dialogue se préoccupe de trouver une définition de la "connaissance", mais finit par n'arriver qu'à une conclusion négative ; plusieurs définitions sont proposées tour à tour et rejetées, mais aucune définition n'est suggérée comme étant satisfaisante.

La connaissance n'est-elle rien d'autre que la perception ?

La première des définitions examinées par Platon, et la seule que je vais considérer, est présentée par Théétète comme suit :

"Il me semble que quelqu'un qui sait quelque chose perçoit la chose qu'il sait, et, pour autant que je puisse dire à présent, la connaissance n'est rien d'autre que la perception."

Socrate identifie cette doctrine avec celle de Protagoras, selon laquelle "l'homme est la mesure de toute chose" ; c'est-à-dire qu'une chose quelconque "est pour moi comme elle m'apparaît, et est pour vous comme elle vous apparaît" [c'est une interprétation différente et plus exacte de la pensée de Protagoras que celle qui dit qu'il voulait dire que "l'homme ne voit que les choses à son échelle"]. Socrate ajoute : "La perception, en conséquence, est toujours quelque chose qui est, et, étant la connaissance, elle est toujours infaillible."

Une grande partie de l'argument qui suit porte sur la caractérisation de la perception ; une fois que ceci est fait, ça ne prend pas longtemps pour prouver que ce que la perception s'est avérée être ne peut pas être la connaissance.

Socrate ajoute à la doctrine de Protagoras la doctrine d'Héraclite, que tout est en perpétuel changement, c'est-à-dire que "toutes les choses dont nous aimons dire qu'elles 'sont', en réalité sont dans un processus évolutif". Platon croit que c'est vrai des objets des sens, mais pas des objets de la réelle connaissance. A travers tout le dialogue, cependant, ses doctrines positives demeurent à l'arrière-plan.

De la doctrine d'Héraclite, même si elle ne s'applique qu'aux objets des sens, jointe à la définition de la connaissance comme étant la perception, il s'ensuit que la connaissance porte sur ce qui devient, pas sur ce qui est.

Arrivé là, quelques énigmes d'un caractère très élémentaire sont abordées. On nous dit que, puisque 6 est plus grand que 4 mais plus petit que 12, 6 est à la fois grand et petit, ce qui est une contradiction. De même, Socrate est à l'heure actuelle plus grand que Théétète qui est un adolescent dont la croissance n'est pas achevée ; mais dans quelques années Socrate sera plus petit que Théétète. Par conséquent Socrate est à la fois grand et petit. Cette idée de proposition relationnelle semble avoir beaucoup troublé Platon, comme elle a troublé tous les grands philosophes jusqu'à Hegel (inclus). Ces énigmes, cependant, ne sont pas centrales dans l'argument et peuvent être ignorées.

Revenant à la perception, c'est regardé comme dû à une interaction entre l'objet et l'organe sensitif, lesquels deux, selon la doctrine d'Héraclite, changent constamment, changeant par là même la perception. Socrate remarque que quand il se sent bien il trouve que le vin est doux, mais quand il est malade, il le trouve aigre. Ici c'est un changement chez celui qui perçoit qui cause le changement de perception.

Critiques de la doctrine de Protagoras

Des objections à la doctrine de Protagoras sont présentées, puis certaines d'entre elles sont retirées. On fait observer que Protagoras aurait dû admettre que les cochons et les babouins sont aussi la mesure de toute chose, puisqu'ils perçoivent eux aussi. Des questions sont soulevées sur la validité de la perception lors des rêves et des crises de folie. On suggère que, si Protagoras a raison, un homme n'en sait pas plus qu'un autre : non seulement Protagoras est aussi sage que les dieux, mais, ce qui est plus sérieux, il n'est pas plus sage qu'un fou. En outre, si les jugements d'un homme valent ceux d'un autre, les gens qui jugent que Protagoras se trompent ont autant de raison d'être considérés comme ayant raison que ne l'est Protagoras.

Socrate s'attache à trouver la réponse à beaucoup de ces objections, se mettant, temporairement, à la place de Protagoras. Pour ce qui est des rêves, les perceptions sont vraies en tant que perceptions. Pour ce qui concerne les cochons et les babouins, c'est rejeté comme un vulgaire abus. Pour ce qui est de l'argument selon lequel, si chaque homme est la mesure de toute chose, un homme est aussi sage qu'un autre, Socrate (-470, -399) propose, toujours en tant que représentant de la pensée de Protagoras (-490, -420), une réponse très intéressante : tandis qu'un jugement honnête ne peut pas être plus authentique qu'un autre, il peut cependant être meilleur, dans le sens qu'il a de meilleures conséquences. Cela suggère le pragmatisme. (C'est vraisemblablement ce passage qui a provoqué l'admiration de F. C. S. Schiller pour Protagoras.)

[Le Théétète est un des dialogues "tardifs" de Platon. On peut penser que la scène qu'il relate prend place vers la fin du Ve siècle, entre la mort de Protagoras (-420) et -- forcément -- celle de Socrate (-399). Le dialogue lui-même a été écrit des décennies plus tard.]

Cette réponse, cependant, bien que Socrate l'ait inventée, ne le satisfait pas. Il fait remarquer, par exemple, que quand un docteur prédit le déroulement à venir d'une maladie, il en sait plus sur le futur que moi. Et quand les hommes ne s'accordent pas sur ce qui est sage de décréter de la part de l'Etat, la question montre que certains hommes ont une plus grande connaissance de l'avenir que d'autres. Ainsi, nous ne pouvons échapper à la conclusion qu'un homme sage est une meilleure mesure des choses qu'un fou.

Toutes ces considérations sont des objections à la doctrine que chaque homme est la mesure de toute chose, et seulement indirectement à la doctrine que "la connaissance" veut dire "la perception", dans la mesure où la première conduit à la seconde. Il y a, toutefois, un argument direct : c'est celui selon lequel la mémoire doit être acceptée autant que la perception. C'est alors admis, et la définition est amendée en conséquence.

Critiques de la doctrine d'Héraclite

Nous arrivons ensuite aux critiques de la doctrine d'Héraclite (-544, -480). Elle est d'abord poussée aux extrêmes (i.e. dans ses retranchements), en accord, nous dit-on, avec la pratique de ses disciples parmi les brillants jeunes gens d'Ephèse. Une chose peut changer de deux manières, par le déplacement, et par un changement de qualité, et la doctrine du flux soutient, est-il expliqué, que toute chose change toujours des deux manières *. Et non seulement chaque chose subit toujours des changements de qualité, mais tout est constamment en train de changer toutes ses qualités -- ainsi, nous dit-on, pensent les gens intelligents à Ephèse. Cela a des conséquences embarrassantes. Nous ne pouvons pas dire "ceci est blanc", car si c'était blanc quand nous avons commencé à parler, ça ne l'est plus avant que nous ayons fini notre phrase. Nous ne pouvons pas avoir raison quand nous disons que nous voyons quelque chose, car voir se transforme constamment en ne pas voir. Si tout change en permanence de toutes les façons possibles, voir n'a pas le droit d'être appelé voir plutôt que ne pas voir, ou la perception d'être appelée perception plutôt que non-perception. En quand nous disons "la perception est la connaissance", nous pourrions aussi bien dire "la perception est la non-connaissance".

* Il semble que ni Platon, ni les brillants jeunes gens d'Ephèse n'aient noté que la locomotion est impossible dans la version extrême de la doctrine d'Héraclite. Le mouvement demande qu'une chose A soit ici maintenant, et là à un autre moment ; elle doit donc rester "la même chose" pendant qu'elle bouge. Dans la doctrine que Platon examine il y a à la fois un changement de place et de qualité, mais pas de changement de substance. A cet égard, la physique quantique moderne va plus loin que n'allaient les disciples d'Héraclite à l'époque de Platon. Platon aurait considéré cela fatal pour la science, mais il s'est avéré que ça ne l'est pas.

[Il est intéressant de noter que les anciens Grecs n'étaient pas à l'aise avec la notion d'invariants dans un modèle dynamique qui lui-même structure nos perceptions. Ou peut-être "philosophaient"-ils pour le plaisir d'agiter des idées, car j'imagine que quand les disciples d'Héraclite rentraient chez eux, ils retrouvaient toutes leurs affaires, leur table, leur bol pour manger, leur lit, et n'étaient pas perturbés outre mesure à l'idée qu'ils les considéraient dans la pratique comme "toujours les mêmes", même s'ils venaient d'argumenter avec d'autres oisifs que ce n'était pas possible... Ce qui est intéressant chez les anciens philosophes grecs, et pour moi surtout chez les présocratiques, ce sont les questions, pas les réponses. Ou en tout cas ces dernières n'ont d'intérêt que pour montrer la progression de leur pensée.]

Besoin que certaines choses ou au moins certains mots soient fixes pour pouvoir parler de quoi que ce soit

Ce à quoi se réduit l'argument ci-dessus est que, quoi que soit d'autre qui soit en flux, le sens des mots doit être fixé, au moins pendant le temps de la discussion, sinon aucune affirmation ne peut être faite, et aucune affirmation n'est plutôt vraie que fausse. Il faut bien qu'il y ait quelque chose de plus ou moins constant, si l'on veut que le discours et la connaissance soient possible. Ceci, je pense, doit être admis. Mais une grande quantité de flux reste compatible avec cette admission.

Il y a, à ce point du dialogue, un refus de discuter de Parménide au motif qu'il est trop important et trop grand. Il est "une figure inspirant la révérence et la vénération". "Il y avait une sorte de profondeur chez lui qui était tout simplement noble".

[On est en train de parler du type qui a affirmé que rien ne bouge... Certes on peut dire "il ne voulait pas dire que rien ne bouge..." mais que "il y a une unité fondamentale dans l'espace et dans le temps, etc."...]

Il est celui "que je respecte au-dessus de tous les autres" [dit Socrate *]. Dans ces remarques, Platon montre son amour pour un univers statique, et son dégoût pour le flux héraclitien qu'il a temporairement admis pour les besoins de la discussion. Mais après cette manifestation de révérence, il s'abstient de développer la pensée de Parménide comme alternative à Héraclite.

* Socrate : Un sentiment de respect me détourne de critiquer sans ménagement Mélissos et les autres qui soutiennent que tout est un et immobile ; mais je sens plus de respect encore pour le seul Parménide. Parménide me paraît être, selon l’expression d’Homère, « à la fois vénérable et redoutable. » J’ai approché l’homme quand j’étais bien jeune encore et lui bien vieux, et il m’a paru avoir une profondeur d’une rare qualité.

Argument final de Platon contre l'identification de la connaissance à la perception

Nous atteignons maintenant l'argument final de Platon contre l'identification de la connaissance avec la perception. Il commence en soulignant que nous percevons à travers nos yeux et nos oreilles, plutôt qu'avec eux, et il continue en soulignant aussi qu'une partie de notre connaissane n'est pas liée à un quelconque organe des sens. Nous savons, par exemple, que les sons et les couleurs sont dissemblables, bien qu'aucun organe des sens ne perçoivent les deux. Il n'y a pas d'organe particulier pour "l'existence et la non-existence, la similitude et la non-similitude, la ressemblance et la différence, et aussi l'unité par rapport aux nombres en général". La même chose s'applique à honorable et déshonorant, et bon et mauvais. "L'esprit contemple certaines choses à l'aide de ses propres instruments, autres que les facultés corporelles des sens." Nous percevons le dur et le mou par le sens du toucher, mais c'est l'esprit qui juge qu'ils existent et qu'ils sont opposés. Seul l'esprit peut atteindre l'existence, et nous ne pouvons pas atteindre la vérité si nous n'atteignons pas l'existence.

Il s'ensuit que nous ne pouvons pas connaître les choses à l'aide seulement des sens, puisqu'à travers les seuls sens nous ne pouvons pas savoir que les choses existent. Par conséquent la connaissance consiste en réflexions, pas en impressions, et la perception n'est pas la connaissance, car elle "ne prend aucune part dans l'appréhension de la vérité, puisqu'elle n'en prend aucune non plus dans l'appréhension de l'existence".

[On notera la faiblesse de cet argument dissimulé derrière un verbiage de phrases qui se répètent les unes les autres parfois comme prémisse parfois comme conclusion.]

Démêler ce qui peut être accepté de ce qui doit être rejeté dans cet argument contre l'identification de la connaissance avec la perception n'est en aucune façon aisé. Il y a trois thèses interconnectées que discute Platon. Ce sont :

(1) La connaissance est la perception ;

(2) L'homme est la mesure de toute chose ;

(3) Tout est dans un état de flux.

Discussion des réfutations par Platon de chacune des trois thèses

(1) La première d'entre elles, avec laquelle l'argument est principalement concerné, n'est pas vraiment discutée seule, sauf dans le passage final que nous avons étudié plus haut. Ici il est soutenu que la comparaison, la connaissance de l'existence, et la compréhension des nombres, sont essentielles à la connaissance, mais ne peuvent pas être incluses dans la perception puisqu'elles ne sont pas concernées par des organes des sens. Ce que l'on peut dire de ces choses est différent. Commençons par la similitude et la dissimilitude.

Similitude et dissimilitude

Que deux nuances de couleur, que je vois, soient similaires ou dissimilaires, selon les cas, est quelque chose que, pour ma part, je dois accepter, non pas comme une "perception" mais comme un "jugement sur une perception". Une perception, je dois dire ["je" ici est Russell], n'est pas une connaissance, mais simplement quelque chose qui se produit [un phénomène], qui appartient à la fois au monde de la physique et au monde de la psychologie. Nous pensons naturellement à la perception, comme le fait Platon, comme à une relation entre un sujet percevant et un objet ; nous disons "je vois cette table". Mais ici "je" et "table" sont des constructions logiques. Le coeur du phénomène, dans sa nudité, est simplement certaines couleurs. Elles sont associées à des images de toucher, elles peuvent provoquer des phrases, et elles peuvent être sources de souvenirs. La perception comme remplie d'images de toucher devient un "objet", qui est supposé être physique ; la perception comme remplie de mots et de souvenirs devient une "perception", qui fait partie d'un "sujet" et est considérée comme mentale. La perception est juste un phénomène ; il n'est ni vrai ni faux ; la perception en tant que qu'elle est remplie de mots est un jugement, et capable de justesse ou de fausseté. Ce jugement, je l'appelle un "jugement de perception". La proposition "la connaissance est une perception" doit être interprétée comme signifiant "la connaissance est un jugement sur une perception". C'est seulement sous cette forme qu'elle est grammaticalement capable d'être correcte.

Pour revenir à la similitude et la dissimilitude, il est tout à fait possible, quand je perçois deux couleurs simultanément, pour que leur similitude ou dissimilitude soit une partie des données, et fasse partie d'un jugement sur une perception. L'argument de Platon selon lequel nous n'avons pas d'organe des sens pour percevoir la similitude et la dissimilitude ignore le cortex, et fait l'hypothèse implicite que tous les organes des sens sont à la surface du corps.

L'argument pour inclure la similitude et la dissimilitude comme des données possibles de perception est comme suit. Faisons l'hypothèse que nous voyons deux nuances de couleur A et B, et que nous jugions que "A est comme B". Faisons l'hypothèse supplémentaire, comme la fait Platon, qu'un tel jugement est en général correct, et, en particulier, est correct dans le cas qui nous intéresse. Il y a alors une relation de similitude entre A et B, et pas simplement un jugement de notre part déclarant la similitude. S'il n'y avait que notre jugement, ce serait un jugement arbitraire, incapable d'être vrai ou faux [ce serait simplement "ce qu'on dit", comme par exemple "je vois les deux couleurs pareilles", ou "je vois les deux couleurs différentes" : ce sont des déclarations qui ne se prêtent pas à une confirmation ou une infirmation]. Etant donné que mon jugement est évidemment capable d'être vrai ou faux, la similitude concerne bien A et B, et n'est pas seulement "mentale". Le jugement "A est comme B" est vrai (s'il est vrai) en vertu d'un "fait", exactement comme le jugement "A est rouge" ou "A est rond". L'esprit n'est pas plus impliqué dans la perception de la similitude que dans celle de la couleur.

[En résumé, avec beaucoup de "philosophisme", R. détruit l'argument de Platon selon lequel la perception n'est pas la connaissance. Un esprit moderne ne se préoccupe pas autant de savoir si la perception est une connaissance ou pas. La perception est un phénomène, et si on prend soin qu'elle ne soit pas trop subjective -- si on s'assure par exemple qu'on puisse la lire sur un cadran -- elle participe à notre modèle du monde extérieur. Elle devient une connaissance. Ceci étant dit ce "monde extérieur" n'est pas totalement indépendant de nos appareils et de nos perceptions -- ça ce serait le Réalisme naïf. Mais ce monde extérieur est construit à travers nos perceptions et mesures. Et ce que nous construisons -- toujours de manière provisoire -- nous l'appelons "la connaissance". Donc la perception est bien, en général, une connaissance.]

Exemple où la perception est trompeuse. En effet A et B ont la même teinte, mais ne sont pas du tout perçus comme tels. Cependant une procédure scientifique (par exemple la mesure avec un appareillage de la teinte de A et de B) permet de la corriger. La science se soucie toujours de transformer des impressions et perceptions qui peuvent être trompeuses en lecture sur un cadran (quand dans un cas l'aiguille marque 3 et dans l'autre 5, il n'est plus question d'impressions trompeuses).

Existence

J'en viens maintenant à l'existence, sur laquelle Platon insiste beaucoup. Nous avons, dit-il, en ce qui concerne les sons et les couleurs, une pensée qui les inclut tous les deux à la fois ; c'est la pensée qu'ils existent. L'existence appartient à toute chose, et fait partie des choses que l'esprit appréhende par lui-même ; sans atteindre l'existence, il est impossible d'atteindre la vérité.

L'argument contre Platon ici est tout à fait différent de celui du cas de la similitude vs la dissimilitude. L'argument ici est que tout ce que dit Platon est de la mauvaise grammaire, ou plutôt syntaxe. Ce point est important, non seulement en relation avec Platon, mais aussi avec d'autres éléments célèbres dans l'histoire de la philosophie comme l'argument ontologique en faveur de l'existence de la Déité.

Supposez que vous disiez à un enfant que "les lions existent, mais les licornes n'existent pas", vous pouvez prouver votre point en ce qui concerne les lions en l'emmenant au Zoo et en lui disant "regarde, ça c'est un lion". Vous n'ajouterez pas, sauf si vous être un philosophe : "Et tu peux voir qu'ils existent." Si, étant un philosophe, vous ajoutez ça, ce que vous dites est dénué de sens. Dire "les lions existent" veut dire "il y a des lions", c'est-à-dire " 'x est un lion' est vrai pour un x bien choisi".

[R. ayant écrit un énorme livre de logique mathématique entre 1900 et 1910 -- qui n'a eu aucune influence chez les mathématiciens -- il lui arrive de se considérer comme un mathématicien, et d'appliquer en philosophie des raisonnements qu'il croit que les mathématiciens utilisent constamment. Là il utilise de la logique propositionnelle booléenne, qui fait partie des fondations de la théorie des ensembles. Un ensemble est formé d'éléments ; on peut décrire l'ensemble en spécifiant chaque élément ; on peut aussi le définir par une propriété (avec des limitations dans sa formulation, cf. "l'ensemble de tous les ensembles qui n'appartiennent pas à eux-mêmes" est exclue, c'est le paradoxe de Bertrand Russell) que doivent satisfaire ses éléments ; il y a l'ensemble vide, etc. ; ça a un intérêt modeste en mathématique en général. C'est intéressant en logique mathématique, qui est une discipline nous disant ce dont on peut parler ou pas, ce qui est démontrable ou pas, fait des observations intéressantes sur le discret et le continu, les équations, etc. Comme R. est par ailleurs un grand esprit, on lui pardonne cette coquetterie.]

Mais nous ne pouvons pas dire de l'x bien choisi qu'il "existe" ; nous utilisons seulement ce verbe pour une description, complète ou incomplète. "Lion" est une description incomplète, car elle s'applique à beaucoup d'objets : "Le lion le plus grand du Zoo" est complet, car cela s'applique à un seul lion.

Maintenant supposez que je sois en train de regarder une chose d'un rouge rutilant. Je peux dire "c'est ma perception à l'instant" ; je peux aussi dire "ma perception présente existe" ; mais je ne dois pas dire "ceci existe" ; la raison en est que le mot 'existe' est signifiant seulement quand il est appliqué à une description par opposition à un nom. Ceci nous débarrasse de l'existence comme l'une des choses dont l'esprit serait conscient dans les objets.

[Oui, enfin c'est surtout du "philosophisme". L'homme pratique dira : "une chose existe quand je peux en voir, ou j'ai des raisons de penser que quelqu'un peut en voir." Le scientifique moderne dira qu'une chose existe quand elle joue un rôle dans un modèle de description de la réalité.

Voici un exemple. Considérons une table vue de dessus, et sous laquelle pour des raisons théoriques il est impossible d'aller voir. Supposons que quand on fait rouler une boule de billard sous la table, elle ressorte toujours exactement comme si elle avait rebondi sous la table contre un large pied cylindrique qu'on ne voit pas.

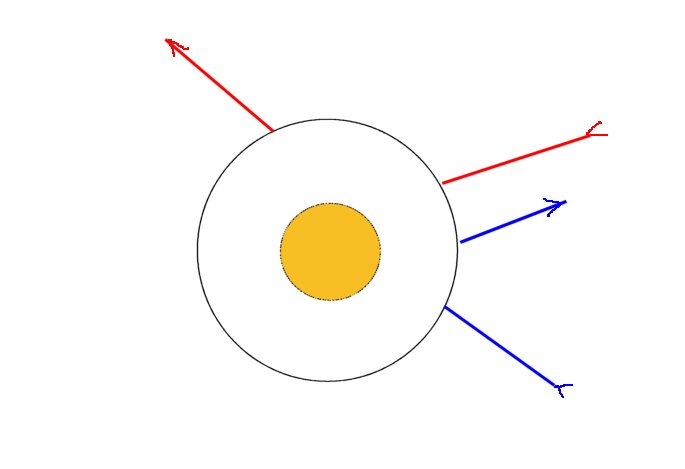
Table qui semble, sous son plateau, avoir un pied cylindrique (en jaune, mais qu'on ne voit pas), car quand on fait rouler des boules sous la table elles ressortent exactement comme si il y avait un pied cylindrique sous la table.

Alors on peut faire l'hypothèse -- mais en fait ce n'est pas une hypothèse, c'est un modèle -- qu'il y a un pied cylindrique sous la table. C'est ainsi qu'on a construit l'hypothèse atomique au début du XIXe siècle pour expliquer des phénomènes en chimie. Max Planck était encore violemment opposé à l'hypothèse atomique en 1880. Ce sont des gens comme John Dalton (1766-1844), en chimie, et Ludwig Boltzmann (1844-1906) en thermodynamique statistique qui ont poussé l'hypothèse atomique. Elle a eu de tels succès explicatifs qu'elle fait maintenant partie de la réalité de la physique.]

Les nombres

J'en arrive maintenant aux nombres. Ici il y a deux notions bien différentes à considérer : d'une part, les propositions en arithmétique, et d'autre part, les propositions empiriques d'énumération. "2 + 2 = 4" est du premier type ; "j'ai dix doigts" du deuxième.

Je conviens avec Platon que l'arithmétique, et les mathématiques pures en général, ne sont pas dérivées de la perception. Les mathématiques pures consistent en des tautologies [une marotte de Russell qui est considérablement réductrice] analogues à "les hommes sont des hommes", mais généralement plus compliquées. Pour savoir si une proposition mathématique est correcte, vous n'avez pas à examiner le monde autour de vous, mais seulement le sens de symboles et suites de symboles ; et les symboles, quand nous nous dispensons des définitions (dont les symboles sont simplement des abréviations), se trouvent pour certains correspondre à des choses qu'on peut voir, pour d'autres à des choses qu'on ne peut pas ou plus voir (comme "Socrate"), et d'autres à des éléments de raisonnement comme "ou", "non", "quels que soient", "certains".

Une équation mathématique affirme que deux groupes de symboles ont le même sens ; et tant que nous nous confinons aux mathématiques, ce sens doit être un sens qui peut être compris sans avoir besoin de connaître quoi que ce soit du monde des perceptions avec les organes des sens. La vérité mathématique, par conséquent, est, comme le dit Platon, indépendante de la perception ; mais c'est une vérité d'une sorte très particulière, concernée seulement pas des symboles.

[R. n'aborde pas la théorie de la preuve. Celle-ci est concernée par la question de savoir ce qu'est une démonstration. Une démonstration est une suite finie de signes parvenant à une tautologie acceptée. Par exemple (a+b)² = a² + 2ab + b², se ramène facilement à 0 = 0, qui est acceptée. Les logiciens de la fin du XXe siècle et début du XXIe, ont montré qu'il y a des propositions arithmétiques très simples indémontrables. C'est même le cas de la plupart d'entre elles. Il est possible que la proposition "il existe une suite infinie de paires de nombres premiers séparés par 2" soit indémontrable et néanmoins vraie.

On est là dans un domaine qui dépasse largement la science mathématique pythagoricienne de Platon, et sans doute aussi la science mathématique de Russell. Mais Pythagore, sans le savoir, avec son théorème qui provient juste de la contemplation des maths de son époque, a lancé la science mathématique. Elle a connu des périodes d'accélération en Occident (de Pythagore jusqu'à Archimède et même Héron, se développant surtout en dehors de la Grèce continentale, en Sicile et à Alexandrie) et de freinage en Occident (3e au 16e siècle, où les grands esprits étaient plus intéressés par la Sainte Trinité que par la modélisation mathématique du monde, même si quelques progrès ont quand même eu lieu, nombres négatifs, Fibonacci, etc.), puis d'accélération à nouveau.]

Les propositions d'énumérations comme "j'ai dix doigts" sont une catégorie bien différente [en fait elles font partie de l'utilisation des mathématiques pour décrire le monde], et sont manifestement, au moins en partie, dépendante de la perception. Clairement le concept de "doigt" est une abstraction provenant de la perception.

[R. recule constamment devant la notion relativement simple à comprendre de modèle de la réalité, sans doute parce qu'à son époque, le Réalisme naïf était encore dominant.]

Mais que dire du concept de "dix" ?

Ici nous semblons être arrivés à une de ces vérités universelles, ou idée platonicienne. Nous ne pouvons pas dire que "dix" est une abstraction à partir des perceptions.

[Bin si !!!]

Car toute perception qui peut être vue comme dix choses, peut également être vue autrement.

Supposons que je donne le nom "digitaire" à tous les doigts d'une main pris dans leur ensemble [pourquoi ne pas les appeler "une main", comme aux cartes ?] ; alors je peux dire "j'ai deux digitaires", et cela décrit le même fait de perception que j'avais décrit précédemment avec l'aide du mot dix.

[Nous sommes ici dans l'un des domaines où la pensée de Russell est bornée, et même contradictoire. En effet, malgré le fait qu'il a longtemps pourfendu dans ses écrits le "Réalisme naïf" (i.e. l'idée que le monde a une structure et une seule, indépendante de la pensée humaine, et que les concepts pour décrire cette réalité appartiennent aussi au monde plutôt qu'à l'esprit humain), il est lui-même, par sa formation philosophique classique à Cambridge en Angleterre à la fin du XIXe siècle, un réaliste naïf -- doublé d'un platonicien.

Dit autrement : il est toujours à la limite de s'échapper du réalisme naïf, comme par exemple quand il dit que cinq doigts c'est aussi une main, et que donc d'une part "cinq" ne résulte pas de la perception (ce qui est tout à fait faux), et d'autre part on a une latitude dans la description des choses (ce qui est tout à fait vrai) ; mais il y retombe toujours, laissant entendre que "bon, mais enfin nos deux mains ça fait quand même dix doigts".

Il fait penser à ce petit garçon mal instruit qui disait "cet immeuble a huit z'étages". On lui faisait remarquer qu'on ne dit pas "huit z'étages" mais "huit t'étages". Il répondait :"Bon, oui, peut-être, mais ça ne change rien au fait qu'il a huit z'étages."]

Ainsi dans l'affirmation "j'ai dix doigts", la perception joue un rôle secondaire, et la conception un rôle prépondérant ; contrairement à ceux qu'elles jouaient dans l'affirmation "ceci est rouge". La question, cependant, n'est que de degré.

La réponse complète, en ce qui concerne les propositions dans lesquelles le mot "dix" apparaît, est que, quand ces propositions sont correctement analysées, on découvre qu'elles ne contiennent aucun constituant correspondant au mot "dix". Expliquer cela dans le cas d'un nombre aussi grand que dix serait compliqué ; remplaçons-le, donc, par "j'ai deux mains". Cela veut dire :

[Nous ne traduisons pas les deux phrases ci-dessous, car ici R. est grossièrement dans l'erreur. Il fait du "philosophisme" de la pire espèce, comme les Scolastiques du XIIIe siècle. En outre dans le cas de R. ce "philosophisme" est appliqué non pas à la Sainte Trinité ou au sexe des anges, mais aux mathématiques -- ce qui est un péché plus grave.

Il se considérait comme un des mathématiciens ayant joué un rôle dans l'établissement de leurs fondations, comme Hilbert, Zermelo, Fraenkel, Frege ou Gödel (lesquels avaient la gentillesse de le traiter cordialement plus ou moins comme l'un des leurs) -- tout ça car il avait à peu près compris le calcul intégral durant ses études à Cambridge et que son prof Whitehead l'aimait bien.

Il a donc même écrit avec Whitehead le gros livre "Principia Mathematica" qui prétendait mettre au net les fondations des mathématiques, mais il y a tout lieu de penser que c'est du philosophisme particulièrement austère appliqué aux maths. Voir par exemple la preuve que 1 + 1 = 2 à la page 86 du deuxième volume

"Preuve" que 1 + 1 = 2 dans "Principia Mathematica" de Russell et Whitehead ]

"There is an 'a' such that there is a 'b' such that 'a' and 'b' are not identical, and whatever 'x' may be, 'x is a hand of mine' is true when, and only when, 'x' is 'a' or 'x' is 'b'."

Here the word "two" does not occur. It is true that two letters 'a' and 'b' occur, but we do not need to know that they are two, any more than we need to know that they are black, or white, or whatever colour they may happen to be.

L'opinion du mathématiciens anglais G.H. Hardy (et de Russell lui-même) sur Principia Mathematica

I can remember Bertrand Russell telling me of a horrible dream. He was in the top floor of the University Library, about A.D. 2100. A library assistant was going round the shelves carrying an enormous bucket, taking down books, glancing at them, restoring them to the shelves or dumping them into the bucket. At last he came to three large volumes which Russell could recognize as the last surviving copy of Principia Mathematica. He took down one of the volumes, turned over a few pages, seemed puzzled for a moment by the curious symbolism, closed the volume, balanced it in his hand and hesitated....

Hardy, G. H. (2004) [1940]. A Mathematician's Apology. Cambridge: University Press. p. 83. ISBN 978-0-521-42706-7.

L'opinion de Kurt Gödel

In his 1944 Russell's mathematical logic, Gödel offers a "critical but sympathetic discussion of the logicistic order of ideas":

"It is to be regretted that this first comprehensive and thorough-going presentation of a mathematical logic and the derivation of mathematics from it [is] so greatly lacking in formal precision in the foundations (contained in *1-*21 of Principia) that it represents in this respect a considerable step backwards as compared with Frege. What is missing, above all, is a precise statement of the syntax of the formalism. Syntactical considerations are omitted even in cases where they are necessary for the cogency of the proofs . . . The matter is especially doubtful for the rule of substitution and of replacing defined symbols by their definiens . . . it is chiefly the rule of substitution which would have to be proved."

Gödel 1944 Russell's mathematical logic in Kurt Gödel: Collected Works Volume II, Oxford University Press, New York, NY, ISBN 978-0-19-514721-6.

Ce que sont les nombres

Ainsi les nombres sont, dans un certain sens précis, formels. Les faits qui vérifient que diverses propositions déclarant que diverses collections partagent toutes la qualité d'être formées de deux membres, ont en commun, non pas un constituant, mais une forme.

En cela elles se différencient des propositions sur la statue de la Liberté, ou la lune, ou George Washington. Ces dernières se réfèrent à des portions particulières de l'espace-temps ; c'est cela qu'ont en commun toutes les déclarations portant sur la statue de la Liberté.

Mais il n'y a rien de commun entre les propositions du type "dans telle situation, tel phénomène, tel objet, on distingue deux éléments", sauf une forme commune.

La relation entre le symbole "deux" (ou 2, ou II, ou ce qu'on veut qui signifie cela) et le sens de la proposition dans laquelle il apparaît est beaucoup plus compliquée que la relation entre le symbole "rouge" et la proposition dans laquelle il apparaît. [On peut tout à fait contester ce "philosophisme" de R.]

Nous pouvons dire, dans un certain sens, que le symbole "deux" ne veut rien dire, car, quand il apparaît dans une affirmation vraie, il n'y a pas de constituant correspondant dans le sens de l'affirmation. Nous pouvons continuer, si nous aimons le faire, à dire que les nombres sont éternels, immuables, et ainsi de suite, mais nous devons ajouter que ce sont des fictions logiques. [Cette conclusion de R. sur les nombres est bien faible.]

Après le concept "deux", le concept "un"

Il y a un autre point. En ce qui concerne les sons et les couleurs, Platon dit "les deux ensembles sont deux, et chacun d'entre eux est un". Nous avons discuté du concept "deux" ; maintenant nous devons considérer le concept "un".

Il y a une erreur analogue à celle concernant l'existence. Le prédicat "un" n'est pas applicable aux choses elles-mêmes, mais seulement à des classes de choses. Nous pouvons dire "la terre a un satellite", mais c'est une erreur syntaxique de dire "la lune est une". Car que peut vouloir dire une telle assertion ? Vous pouvez aussi bien déclarer "la lune est plusieurs" puisqu'elle a plusieurs parties. Dire que "la terre a un satellite" est attribuer une propriété au concept "satellite de la terre" ; il s'agit de la propriété suivante :

"Il y a un 'c' tel que 'x est un satellite de la terre' est vraie et seulement vraie quand 'x' est 'c'."

[Il est consternant que R. termine son chapitre -- qui est sans doute l'un des plus importants de tout son livre -- par des considérations aussi faibles. Il veut simplement dire que 'l'ensemble des satellites de la terre est de cardinal 1', c'est-à-dire a un seul élément, c'est-à-dire 'la terre a un satellite et un seul'... Pas besoin d'écrire un chapitre entier de "philosophismes" pour parvenir à ça.

Ce qui est plus consternant encore, c'est que ce genre de considérations, que R. lui-même a pourfendues quand il a dit que l'un des drames de la philosophie était d'avoir voulu appliquer les raisonnements mathématiques de Pythagore à la métaphysique, se donnent en spectacle aux esprits faibles comme s'il s'agissait de raisonnements sophistiqués et profonds.

En outre les mathématiques parviennent effectivement de temps à autre à des conclusions stupéfiantes au terme de raisonnements sophistiqués et profonds, mais R. ne les connaît pas, et -- y compris en logique -- ils n'ont rien à voir avec ces enfantillages.]

Il s'agit d'une vérité astronomique ; mais si à la place de "un satellite de la terre" vous mettez "la lune" ou n'importe quel autre nom propre, le résultat devient soit dénué de sens soit une tautologie. "Un", par conséquent, est une propriété de certains concepts, juste comme "dix" est une propriété du concept "mon doigt". Mais prétendre que ""la terre a un satellite (la lune), donc la lune est une" est aussi fautif que de dire "les Apôtres étaient douze ; Pierre était un apôtre ; donc Pierre était douze" -- ce qui deviendrait cependant correct si au lieu de "douze" on utilisait une qualité comme "blanc".

Les considérations ci-dessus ont montré que, tandis qu'il y a effectivement une sorte de connaissance formelle, celle de la logique et des mathématiques, qui ne découle pas de la perception, les arguments de Platon relatifs à toutes les autres formes de connaissance sont fallacieux. Cela ne prouve pas, bien sûr, que ses conclusions soient fausses ; cela prouve seulement qu'il n'a apporté aucune raison valide pour les considérer comme vraies.

(2) J'arrive maintenant à la position de Protagoras, que l'homme est la mesure de toute chose, ou, comme c'est interprété, que chaque homme est la mesure de toute chose. Ici il est essentiel de décider du niveau auquel la discussion doit se dérouler. Il est évident par exemple, pour commencer, que nous devons distinguer entre les perceptions et les inférences. Parmi les perceptions, chaque homme est inévitablement confiné dans son corps ; ce qu'il sait des perceptions des autres il le sait par inférence à partir de ses propres perceptions (i.e. ce qu'il entend ou lit qu'on lui dit). Les perceptions des rêveurs et des fous, en tant que perceptions sont aussi bonnes que les autres ; la seule objection est que, comme leur contexte est inhabituel, elles entraînent facilement des inférences fallacieuses. [Encore du "philosophisme" (!) au lieu de dire simplement : "on écarte les rêveurs et les fous."]

Mais qu'en est-il des inférences ? Sont-elles également privées et personnelles ? Dans un sens, nous devons admettre qu'elles le sont. Ce que je crois, je le crois parce qu'une certaine raison me paraît attrayante. Il est vrai que ma raison peut être l'affirmation de quelqu'un d'autre, mais ça peut être une excellente raison -- par exemple, si je suis un juge qui écoute des témoignages.

[Noter que R. est toujours au bord de tomber dans le subjectivisme radical, mais il l'évite chaque fois, avec des arguments spécieux, car il sait que ça ne mène pas à grand chose d'intéressant. Certains philosophes que nous étudierons, au XVIIIe siècle, comme Berkeley ou Fichte, étaient des partisans du subjectivisme radical. John Stuart Mill pratiquait un subjectivisme plus modéré.]

Et quel que soit l'attrait qu'a pour moi la doctrine de Protagoras, il est raisonnable d'accepter, par exemple, l'opinion d'un comptable quand il s'agit de comprendre des chiffres économiques plutôt que ma propre opinion [manifestement R. n'a jamais fait tourner d'entreprise ; la pire attitude pour un patron est de s'en remettre les yeux fermés aux comptables pour produire et interpréter les chiffres], car je peux avoir constaté à plusieurs reprises qui si nous étions en désaccord c'était généralement lui, après examen plus approfondi, qui avait raison.

Dans ce sens, je peux admettre qu'un autre homme soit plus sage que moi. La position protagoricienne, interprétée correctement, n'implique pas que je ne fasse jamais d'erreur, mais seulement que je doive me rendre compte de mes erreurs. Mon passé peut être jugé exactement comme si c'était une autre personne qui était jugée. Mais tout ceci présuppose qu'en ce qui concerne les inférences, par opposition aux perceptions, il y a certains standards impersonnels, c'est-à-dire neutres, de correction.

Si l'on pense qu'une inférence que je fais est juste aussi bonne que celle de quelqu'un d'autre, alors l'anarchie intellectuelle que Platon déduit de Protagoras s'ensuit effectivement. Sur ce point, par conséquent, qui est important pour moi, Platon me semble correct. Mais l'empiriste dirait que les perceptions sont le test de la correction dans l'inférence à partir de matériau empirique.

[Nous verrons plus tard le subjectivisme. Disons simplement, pour l'instant, que chaque homme est en définitive seul pour choisir ce qu'il pense ou pas. Il se construit la compréhension du monde qu'il veut. Il a ses propres critères de raison, de cohérence (si c'est important pour lui) et de folie. Le plus souvent sa compréhension est très éloignée du solipsisme. Au contraire elle fait jouer un rôle important aux autres -- parfois trop important, chez les esprits timorés, sans énergie vitale ou pour quelqu'autre raison que ce soit prompts à être embrigadés. C'est une question importante, avec beaucoup d'aspects et d'implications, surtout au XXe siècle qui a vu la montée des totalitarismes. Nous y reviendrons.]

(3) La doctrine du flux universel est caricaturée par Platon, et il est difficile de supposer que quiconque ait jamais soutenu la forme extrême qu'il lui donne. Supposons, par exemple, que les couleurs que nous voyons soient continuellement en train de changer. Un mot comme "rouge" s'applique à beaucoup de nuances de couleur, et si nous disons "je vous du rouge", il n'y a pas de raison que cela ne reste pas le cas pendant tout le temps que ça prend pour le dire. Platon obtient ses conclusions en appliquant à des processus de changement continuel des oppositions logiques comme percevoir et ne pas percevoir, savoir et ignorer. De telles oppositions, cependant, ne sont pas adaptées pour décrire des processus de ce type. Supposez, qu'un jour brumeux, vous regardiez un homme s'éloignant de vous sur une route : il devient de plus en plus difficile à discerner, et arrive un moment où vous êtes sûr que vous ne le voyez plus, mais il y a une période intermédiaire de doute. Les oppositions logiques ["de deux choses l'une, soit tu le vois, soit tu ne le vois pas"] ont été inventé par commodité, tandis que les changements continus requièrent un appareillage quantitatif, une possibilité que Platon ignore. Ce qu'il dit par conséquent sur la question est essentiellement hors sujet.

En même temps, il faut admettre que, sauf si les mots, jusqu'à un certain point, avaient un sens parfaitement fixe, tout discours deviendrait impossible. Ici encore, cependant, il est aisé d'être trop absolu. Le sens des mots évolue ; prenez par exemple le mot "idée". C'est seulement par un processus considérable d'éducation que nous parvenons à donner à ce mot un sens proche de la signification que Platon lui conférait. Il est nécessaire que les changements dans le sens des mots soient plus lents que les changements dans ce que les mots décrivent ; mais il n'est pas nécessaire qu'il n'y ait aucun changement dans le sens des mots. Peut-être que ces remarques ne s'appliquent pas aux mots abstraits utilisés en logique et en mathématiques, mais ces derniers, nous l'avons vu, s'appliquent seulement aux formes, pas à la matière, des propositions. Ici encore nous découvrons que la logique et les mathématiques sont des disciplines intellectuelles spéciales. Platon, sous l'influence des Pythagoriciens, assimilait trop les autres savoirs aux savoirs mathématiques. Il partage cette erreur [appliquer l'axiomatique et les raisonnements mathématiques à la métaphysique] avec nombre des plus grands philosophes, mais ce n'en est pas moins une erreur.