Cours de mathématiques de 2e

Trigonométrie : cercle trigonométrique, fonctions circulaires

Texte

On a étudié, en classe de quatrième, les sinus, cosinus et tangente comme des rapports de longueurs dans des triangles rectangles. On a même introduit l'idée de cosinus négatif pour un angle θ compris entre π/2 et π, afin de donner une validité au théorème d'Al-Kashi dans tous les cas de figures. (Si vous avez besoin de vous rafraîchir la mémoire les leçons étaient ici : sinus, et cosinus et Al-Kashi).

Cercle trigonométrique. Maintenant on va étendre ce qu'on a appris à tous les angles, à l'aide, dans un repère habituel, du cercle centré à l'origine et de rayon 1, sur lequel on va regarder des angles orientés.

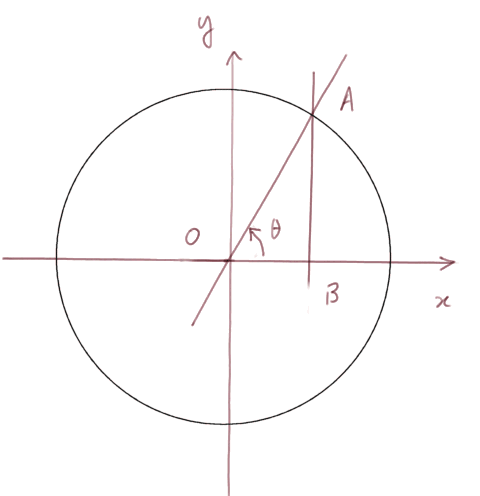
On nomme ce cercle du grand mot de "cercle trigonométrique". Mais ça ne signifie rien de plus que : on va étudier les fonctions trigonométriques à l'aide de points sur ce cercle.

Ainsi, soit l'angle θ représenté ci-dessus. Alors

• sinθ = ordonnée du point A
• cosθ = abscisse du point A

Quelques sinus, cosinus et tangente à retenir.

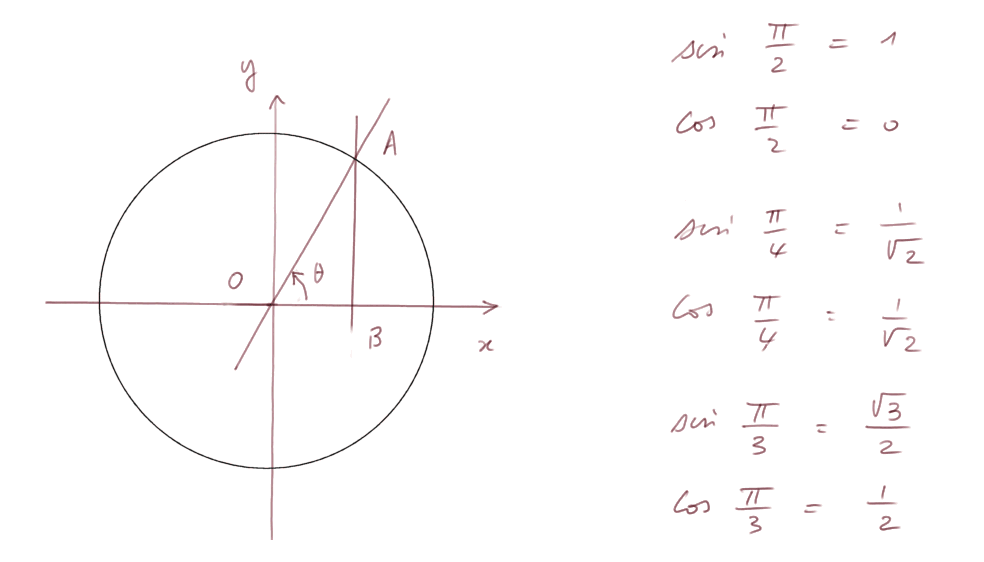
et aussi,

• tan (π/4) = 1
• tan (π/2) n'existe pas

Valeurs négatives. Maintenant les sinus et cosinus étant définis comme des coordonnées de points, ils peuvent être positifs ou négatifs.

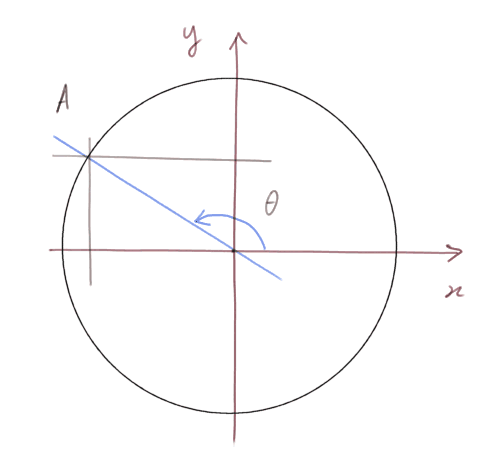
Par exemple sin(5π/6) = 1/2, et cos(5π/6) = -(√3)/2.

Si 0 ≤ θ ≤ π, sinθ est positif.

Si π/2 ≤ θ ≤ 3π/2, cosθ est négatif.

Quand θ est entre π et 3π/2, le sinus et le cosinus sont tous les deux négatifs.

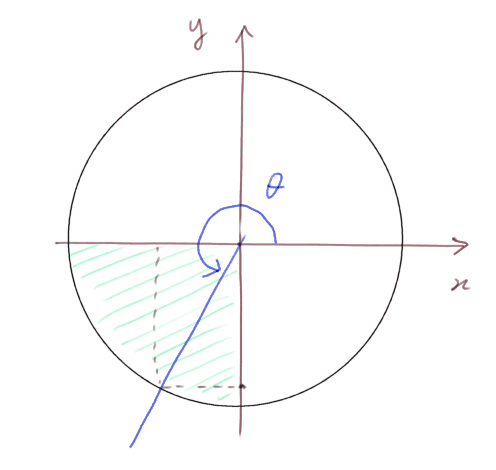
Et quand θ est dans le quatrième quadrant (en bas à droite) le cosinus est positif, et le sinus est négatif.

Fonctions sinus et cosinus. Les fonctions sin : θ -> sinθ et cos : θ -> cosθ sont donc deux fonctions de R vers [ -1 ; 1 ].

Voici le graphe de la fonction sinus

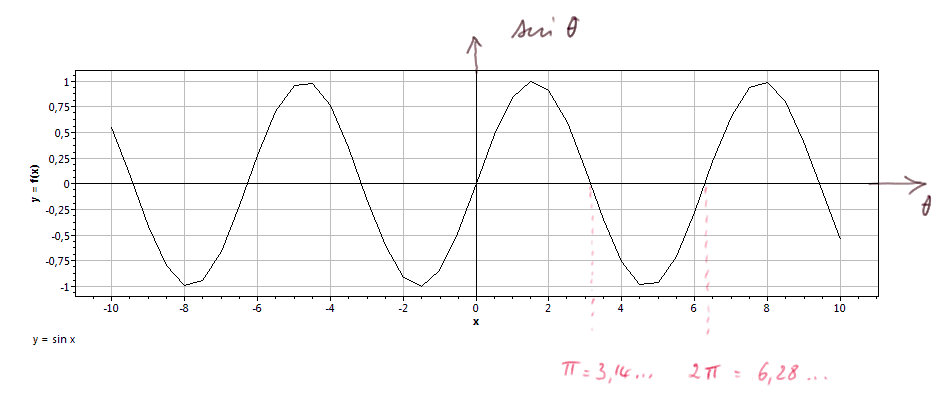
et le graphe de la fonction cosinus

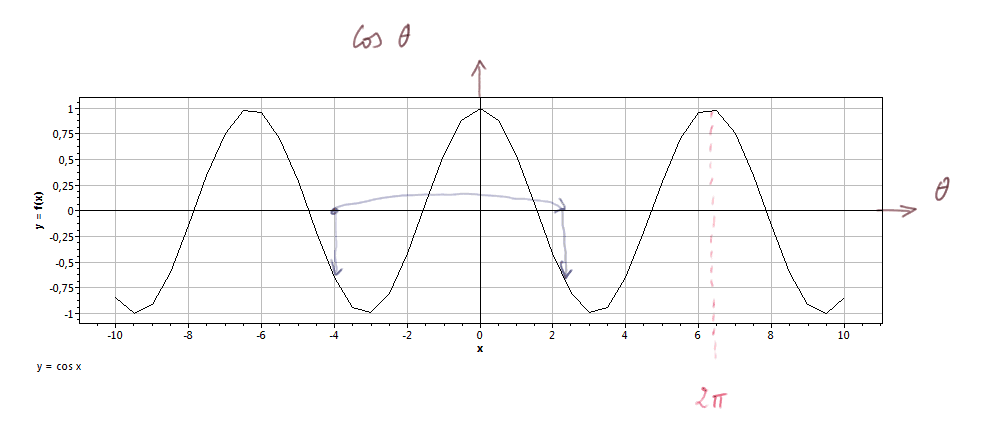
Ce sont deux fonctions relativement simples :

• elles sont ce que l'on appelle "périodiques", c'est-à-dire que quel que soit θ, on a sinθ = sin(θ + 2π). Idem pour cosinus
  
  
• elles sont identiques à une translation près. Etant donné que cosθ = sin(θ + π/2), le graphe de la fonction cosinus est le graphe de la fonction sinus décalé de π/2 vers la gauche (ou aussi, si l'on préfère, de 3π/2 vers la droite).

Fonction tangente. Sur le cercle trigonométrique, la tangente de l'angle θ est simplement l'ordonnée du point A divisée par l'abscisse du point A.

On peut aussi écrire

Cette fonction est définie pour toutes les valeurs de θ dans R, sauf π/2 et tous les nombres obtenus en rajoutant ou retranchant un multiple de π à π/2. Voici son graphe :

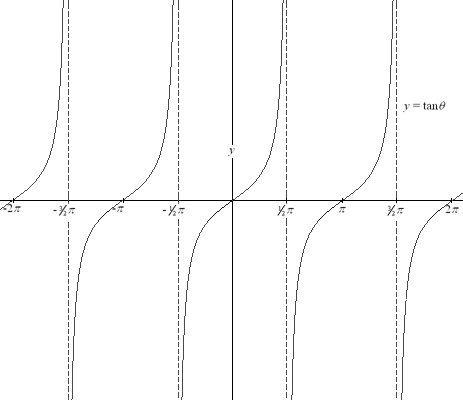
(source : site de l'université de Nipissing au Canada, http://nipissingu.ca)

La fonction tanθ est périodique, de période π. C'est-à-dire que pour n'importe quel angle θ (différent de... -π/2, π/2, 3π/2, etc.), on a tanθ = tan(θ + π).

Nouvelles "fonctions usuelles". Les fonctions sinus, cosinus et tangente (et quelques autres) sont des nouvelles fonctions usuelles pour nous.

• Elles ne sont pas définies par des polynômes, mais par de la géométrie.
  
  
• On verra d'autres façons de les définir, écrire et manipuler (à l'aide de séries de polynômes en x convergeants vers les fonctions trigonométriques)
  Par exemple, on verra que quel que soit x, on a
  
  
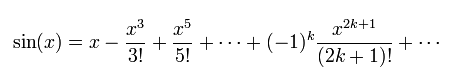
  (source : wikipedia)
  
  Le signe n! est une notation pour "le produit de tous les entiers de 1 jusqu'à n". Ainsi 5! = 1 x 2 x 3 x 4 x 5 = 120.
  
  
• Elles joueront un rôle étonnamment important dans toutes les branches des mathématiques, depuis l'arithmétique jusqu'aux nombres complexes, et aussi en physique.

Formules importantes. Pour terminer, voici deux formules importantes concernant les sinus et cosinus de somme d'angles. On pourrait les démontrer par la géométrie élémentaire, mais nous les démontrerons plus tard à l'aide de méthodes beaucoup plus puissantes utilisant les nombres complexes.

Quels que soient les angles θ₁ et θ₂ , on a :

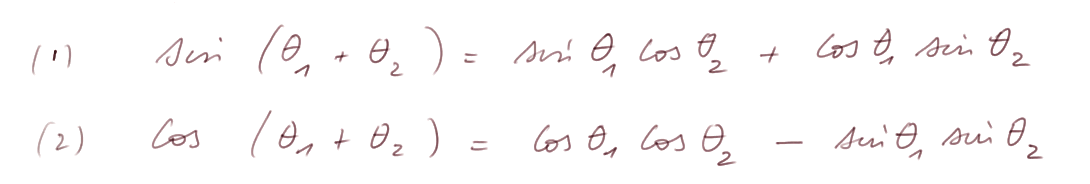
Noter cependant que l'identité (2) est une conséquence de l'identité (1) en utilisant le fait que cosθ = sin(θ + π/2).

Exercices :

1. Montrer que, quel que soit θ, on a sin(-θ) = -sinθ
2. Montrer que, quel que soit θ, on a cos(-θ) = cosθ
3. Démontrer l'identité (2) ci-dessus sur les fonctions trigonométriques de sommes, à l'aide de l'identité (1) et le fait que, quel que soit θ, on a cosθ = sin(θ + π/2).

Les écrans de la vidéo

écran 1
écran 2
écran 3
écran 4
écran 5
écran 6
écran 7
écran 8
écran 9
écran 10
écran 11
écran 12
écran 13

Plan général du cours

Contacter le professeur