Mathematics course : 6th grade

How to split a cube into 3 identical pyramids

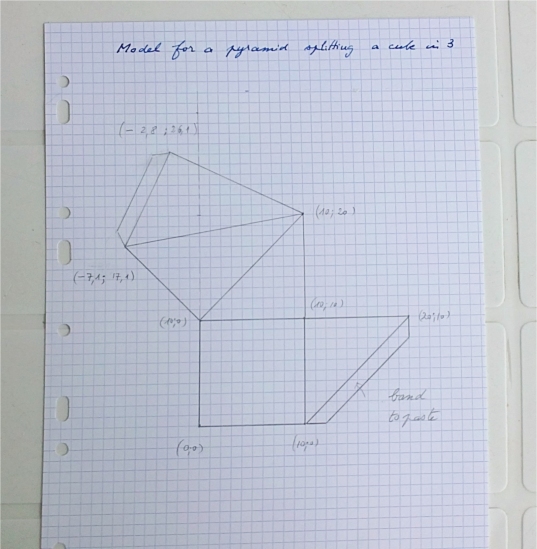
Text

We shall build with graph cardboard, a pair of scissors, and glue a pyramid fitting into a cube.

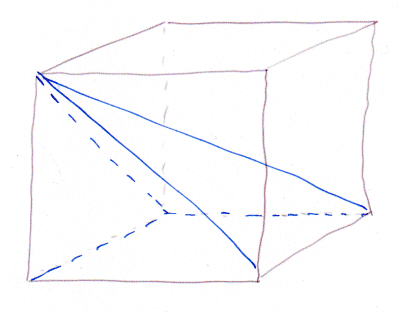
The base of the pyramid will be the bottom side of the cube, and the top of the pyramid will be one of the top corners of the cube.

We shall see that the volume of this pyramid is exactly 1/3 of the volume of the cube. Moreover, we shall reconstruct the cube with three identical pyramids like this one.

To build the pyramid, we begin with a model (see video for details).

Click on image to enlarge

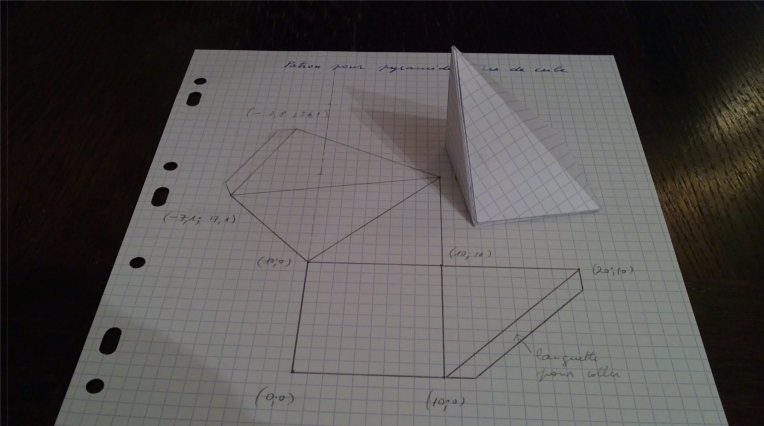
We cut the sheet according to the model.

And we fold and paste to get a pyramid.

We build 3 pyramids on the same model. And we can see that they fit exactly into a cube.

Do the three pyramids fill in the cube entirely ? Or could there be a void inside ? Reasoning on the angles of the various planes, on sees that there can be no void inside. The cube is fully filled.

Therefore the volume of the initial pyramid is a third of the volume of the cube. Hence it is the product of the surface area of its base times its height divided by 3.

We can write : V = S x h x 1/3
(where V is the volume of the pyramid, S is the surface area of its base, that is one of the sides of the cube, and h the height, that is an edge of the cube).

We shall use this result to extend it to any kind of pyramid, and even to any cone.

This result is the generalisation to 3 dimensions of the following well known fact in the plane concerning the surface area of triangles: the surface area of a triangle is the product of the length of any side by the opposite height divided by 2.

In 3D we have the "same" fact but with the factor 1/3 instead of 1/2, that is: the volume of any pyramid is the product of the surface area of its base by the opposite height divided by 3.

Digression: Here is another elementary calculation of the volume of the pyramid. (By "elementary" we mean "without using integral calculus".) We only sketch it. Think of the pyramid as made of a large number of small cubes arranged in stories of decreasing square size. The bottom story would be made of n² small cubes, the next story of (n-1)² cubes, the next one of (n-2)², etc. up to the top story of only one small cube. Such a pyramid contains 1 + 4 + 9 + 16 + ... + n² small cubes. Calculations show that 1 + 4 + 9 + 16 + ... + n² = n(n+1)(2n+1)/6. (If we call this number V(n), it is easy to check that V(n) - V(n-1) = n².) So the ratio of the volume of the pyramid to the whole large cube is n(n+1)(2n+1)/(6n³). When n becomes larger and larger, and the pyramid made of small cubes is smoother and smoother, this ratio tends to 1/3.

Now a bit of fun to finish the lesson: let's place ourselves in a 4D space. Consider a 3D cube in this space, and a point P outside the 3D space in which the cube lies (OK, it's a bit difficult to visualise :-). Let's draw the lines from P to all the points in the 3D cube. We obtain a 4 dimensional figure. The 4D-volume measurement of this 4D figure is the product of the 3D-volume of the 3D cube by the opposite height divided by 4. And four such identical hyper-pyramids can be assembled into a hyper-cube.

Here is some help to visualise and work in 4 dimensions.

At the end of high school, when we study integral calculus, the fact that the hyper-pyramid has (hyper-)volume 1/4 of the hyper-cube will become an easy result, stemming from the fact that integral from 0 to z of x³ is z⁴/4. With z=1 this yields 1/4. To establish that four hyper-pyramids can be fitted into a hyper-cube will still require a bit of reasoning.

Exercise:

Try to draw on a sheet of paper the cube with its three fitting pyramids inside.

Answer

The screens of the video

screen 1
screen 2
screen 3
screen 4
screen 5
screen 6
screen 7
screen 8
screen 9
screen 10
screen 11

Contact

Answer: we discover that the drawing looks terribly messy. That's why we built the pyramids with cardboard and glue.