L'essor de la science

---------------------------------------------------------------------------------------

publicité

---------------------------------------------------------------------------------------

III.1.6 : L'ESSOR DE LA SCIENCE

Presque tout ce qui distingue le monde moderne des siècles qui l'ont précédé est attribuable à la science, qui atteignit ses plus spectaculaires triomphes au 17e siècle. La Renaissance italienne, tout en n'étant plus médiévale, n'est pas moderne ; elle ressemble davantage à la meilleure époque de la Grèce. Le 16e siècle, avec ses préoccupations théologiques, est lui-même plus médiéval que le monde de Machiavel [c'est le décalage dont on a déjà parlé entre la Renaissance italienne et celle au nord des Alpes].

Le monde moderne, en ce qui concerne sa tournure d'esprit générale, commença avec le 17e siècle. Platon ou Aristote auraient pu comprendre les idées des Italiens de la Renaissance; Thomas d'Aquin aurait été horrifié par les vues théologiques de Luther, mais il les aurait comprises.

Avec le 17e siècle c'est différent : Platon et Aristote, Aquin et Occam, n'aurait absolument rien compris aux théories scientifiques de Newton.

[On notera qu'un phénomène comparable s'observe au 20e et 21e siècle : les esprits éduqués, dont les "philosophes", et même une partie du grand public comprennent à peu près la science des trois siècles jusqu'à 1900 (en le disant vite pour les "philosophes" actuels) ; mais ils ne comprennent rien à la théorie de la relativité générale, à la mécanique quantique, et surtout aux idées du début du 21e siècle en physique fondamentale, ainsi qu'en mathématiques. (L'un des drames de l'enseignement français est que les cursus de philosophie avancés ne contiennent pas de sciences sérieuses.)

Ou en tout cas, la sophistication de la science actuelle est inaccessible aux esprits même de bonne culture générale, s'ils n'ont pas fait d'études avancées dans les domaines scientifiques.

Ce qui ne veut pas dire que la science, qui a conduit à la Révolution industrielle et à la technologie, à la consommation de masse, au welfare state, à la pollution généralisée, et aux masses manipulées par des médias consternants et odieux, ne soit pas sans défauts.]

Les nouvelles conceptions que la science introduisit influencèrent profondément la philosophie. Descartes, qui fut en un certain sens le fondateur de la philosophie moderne, fut lui-même l'un des créateurs de la science du 17e siècle. Il nous faut dire quelques mots des méthodes et résultats en astronomie et en physique, avant que l'atmosphère intellectuelle de l'époque dans laquelle la philosophie moderne débuta puisse être comprise.

Quatre grands hommes -- Copernic, Kepler, Galilée, et Newton -- ont joué un rôle de premier plan dans la création de la science. L'un d'eux, Copernic, appartient au 16e siècle, mais à son époque il eut peu d'influence.

Copernic

Copernic (1473-1543) était un ecclésiastique polonais, d'une orthodoxie impeccable. Dans sa jeunesse il voyagea en Italie, et absorba quelque chose de l'atmosphère de la Renaissance. En 1500 il avait une position de lecteur ou professeur de mathématiques à Rome, mais en 1503 il retourna dans son pays d'origine, où il fut chanoine de Frauenburg. Il semble avoir consacré la plus grande partie de son temps à combattre les Allemands et à réformer la monnaie, mais ses loisirs étaient consacrés à l'astronomie. Il en vint à penser que le Soleil était au centre de l'univers, et que la Terre avait deux mouvements : une rotation quotidienne sur elle-même, et une révolution annuelle autour du Soleil. La crainte de la censure ecclésiastique le conduisit à repousser la publication de ses idées, bien qu'il permît qu'elles devinssent connues. Son ouvrage principal, De Revolutionibus Orbium Caelestium, fut publié l'année de sa mort (en 1543), avec une préface de son ami Osiander disant que la théorie héliocentrique n'était proposée qu'à titre d'hypothèse. On n'est pas sûr si Copernic avait approuvé cette déclaration, mais la question n'est pas très importante, puisque lui-même dit des choses comparables dans le corps de l'ouvrage. (Voir "Three Copernican Treatises", traduit vers l'anglais par Edward Rosen, Chicago, 1939.) Le livre de Copernic est dédié au pape, et échappa à la condamnation officielle de l'Eglise catholique jusqu'à l'époque de Galilée. L'Eglise, du vivant de Copernic était plus libérale que ce qu'elle devint après que le concile de Trente, les Jésuites, et l'Inquisition renouvelée eurent fait leur travail.

La tonalité du travail de Copernic n'est pas moderne ; on pourrait plutôt le décrire comme pythagoricien. Il considère comme un axiome que tous les mouvements célestes sont circulaires et uniformes [en vitesse angulaire], et comme les Grecs il s'autorise à prendre en considération des motivations esthétiques [c'est moins idiot que R. veut le faire entendre, voir le livre de Graham Farmelo "It must be beautiful" expliquant que bcp de savants modernes tiennent compte de l'esthétique dans l'élaboration de leurs équations].

Il y a encore des épicycloïdes dans son système, mais leurs centres sont au Soleil, ou, plutôt, près du Soleil. Le fait que le Soleil ne fût pas exactement le centre gâcha la simplicité de sa théorie.

Copernic ne semble pas avoir été au courant de la théorie héliocentrique d'Aristarque de Samos (-310, -230), mais il n'y a rien dans ses spéculations que n'eût pu trouver l'astronome grec.

Ce qui est important dans le travail de Copernic c'est le détrônement de la Terre de son éminence géométrique. A long terme, cela rendait difficile de donner à l'homme l'importance cosmique que lui assigne la théologie chrétienne. Mais de telles conclusions auraient été rejetées par Copernic lui-même, dont l'orthodoxie était sincère, et qui protestait quand on lui disait que ses vues étaient en contradiction avec la Bible.

Il y avait de vraies difficultés dans la théorie copernicienne. La plus grande était l'absence de parallaxe stellaire dans les observations réelles. Si la Terre, à n'importe quel moment de son orbite, est à 930 millions de kilomètres [chiffre moderne ; Russell, citant Copernic il faut croire, parle de 300 millions de km] du point où elle sera dans six mois, cela devrait causer un décalage dans les positions apparentes des étoiles. On observe le même phénomène quand on regarde un bateau depuis la côte : si à partir d'un point A il s'éloigne exactement dans la direction du Nord par rapport à A, alors vu d'un point B qui n'est pas sur la ligne A-Nord, le bateau ne donnera plus l'impression d'aller dans une direction fixe par rapport à B. [L'explication de Russell est trop compliquée. Il suffit de dire que si la Terre, une étoile F et une étoile G sont presque alignées à une certaine date de l'année, alors six mois plus tard elles ne devraient plus l'être.]

Or on n'observait aucune parallaxe [en astronomie, à l'époque de Copernic], et Copernic en déduisit correctement que les étoiles fixes [on les supposait fixes aussi à son époque] devaient être beaucoup plus éloignées que le Soleil. Ce n'est pas avant le 19e siècle que les techniques de mesure devinrent suffisamment précises pour que la parallaxe stellaire puisse être observée, et seulement pour les étoiles les plus proches.

[On ne voit pas à quelle "difficulté" R. fait référence. Copernic lui-même expliquait l'absence d'observation de parallaxe.]

Une autre difficulté était liée à la chute des corps. Si la Terre était continuellement en rotation de l'ouest vers l'est, un corps qu'on laissait tomber d'une certain hauteur aurait dû ne pas arriver à la verticale du point d'origine de sa chute, mais un peu plus à l'ouest, puisque la Terre aurait un peu tourné durant la chute. La réponse à cette difficulté fut trouvée par Galilée avec sa loi d'inertie, mais à l'époque de Copernic il n'y avait pas d'explication.

[Les "explications" de R. sont une fois de plus cryptiques. Il veut sans doute dire que localement l'expérience de chute peut être considérée comme prenant place dans un champ gravitationnel uniforme, que la Terre se déplace linéairement vers l'est, et que le corps même au début de sa chute a de toute façon le même mouvement horizontal que la Terre, et qu'il le conserve par inertie. Donc sa chute verticale ne le révèle pas. Russell n'était pas un physicien, ni un mathématicien, mais un philosophe, et surtout un prodigieux expositeur de l'histoire des idées.]

La science moderne et ses derniers critiques

Il y a un livre intéressant de Edwin Arthur Burtt (1892-1989), intitulé "The Metaphysical Foundations of Modern Physical Science" (1925), qui présente avec beaucoup de force de persuasion toutes les hypothèses périlleuses [vues de leur époque] que faisaient les hommes qui ont fondé la science moderne. Il souligne avec justesse qu'il n'y avait à l'époque de Copernic aucun fait connu qui aurait clairement forcé à adopter son système, et en revanche qu'il y en avait plusieurs qui militaient contre.

"Les empiristes contemporains, s'ils avaient vécu au 16e siècle, auraient été les premiers à se moquer de la nouvelle philosophie de l'univers [présentée par Copernic]." L'objectif général du livre de Burtt est de discréditer la science moderne en suggérant que ses découvertes sont des accidents chanceux résultant de croyances superstitieuses tout aussi ridicules que celles du Moyen Âge.

Je pense que la thèse de Burtt montre une misconception de sa part de ce qu'est l'attitude scientifique : ce n'est pas ce qe croit l'homme de science qui le distingue [des savoirs antiques et médiévaux], mais comment et pourquoi il parvient à ses croyances [qui, comme l'a fait observer Popper -- et il est devenu de manière incompréhensible célébrissime pour avoir énoncé cette évidence --, ne sont jamais que provisoires. Ce sont des inductions, à la Occam, à partir des faits d'observation. On les utilise ensuite pour prévoir d'autres faits. Et quand elles prévoient qqc qu'on n'observe pas, on s'en débarrasse pour les remplacer par de meilleures.]

Les croyances du scientifique sont toujours provisoires, jamais dogmatiques [en théorie...] ; elles sont fondées sur ce qu'on observe [et construites par induction], par sur l'autorité ou l'intuition [euh, si parfois... Induction et intuition ne sont pas très différentes.] Copernic avait raison d'appeler sa théorie une hypothèse ; ses opposants avaient tort de penser que des nouvelles hypothèses étaient indésirables.

[Pourquoi R. progresse-t-il de manière si pédestre dans les débuts de la science ? La raison est qu'il prépare le terrain pour la philosophie qui suivra et qui sera profondément influencée par la science. Les connaissances antiques et médiévales étaient assez différentes de la science moderne Il est bon de le rappeler, même si aujourd'hui les méthodes intellectuelles de la science nous paraissent comme aller de soi. Pendant des millénaires, le savoir était soit "révélé", soit ayant l'autorité des Anciens, et était presque toujours dogmatique.

L'un des aspects du "miracle grec" est que pendant 1 ou 2 siècles, avant le trio infernal Socrate/Platon/Aristote, l'homme grec s'est interrogé sur l'univers sans préconceptions et a fait des progrès fabuleux dans sa compréhension du monde. Puis ça s'est arrêté, pour se focaliser sur l'éthique, la politique, l'immortalité, l'au-dela où se serait mieux, la vertu, le bien vs le péché, l'Un, le Nousse et l'Âme, Dieu, la chair diabolique, la Sainte-Trinité, le sexe des anges, etc.

La philosophie antique et médiévale était par conséquent aussi très différente de celle que nous étudierons ensuite.]

Les mérites des premiers scientifiques : patience dans les observations des faits, et audace dans les hypothèses explicatives

Les hommes qui fondèrent la science moderne avaient deux mérites, qui ne se rencontraient pas nécessairement ensemble : une immense patience dans l'observation, et une grande audace dans l'élaboration d'hypothèses. Le second de ces mérites avaient déjà appartenu aux plus anciens philosophes grecs ; et le premier existait, très développé, chez les astronomes de l'Antiquité tardive. Mais aucun parmi les Anciens, à l'exception possible d'Aristarque de Samos, ne possédait les deux mérites, et au Moyen Âge les penseurs n'avaient ni l'un ni l'autre. Copernic, lui, comme ses grands successeurs, possédait les deux..

Il savait tout ce qui pouvait être connu, à l'aide des instruments existants à son époque, sur les mouvements apparents des corps célestes sur la ou les sphères célestes, et il sentait que l'hypothèse de la rotation de la Terre sur elle-même était plus économique que l'hypothèse d'une révolution de toutes les sphères célestes.

Selon le point de vue moderne, qui regarde tout mouvement comme relatif, la simplicité est le seul gain apporté par cette hypothèse [de la rotation de la Terre sur elle-même ; prendre un point ou un autre comme fixe donne des calculs différents et parfois l'un est plus simple que les autres, voir calculs de la rencontre entre la voiture de Pépé et celle de son petit-fils Kevin.

Mais la relativité galiléenne du mouvement n'était pas encore un concept maîtrisé à l'époque de Copernic.

En ce qui concerne la rotation annuelle de la Terre autour du Soleil, c'est là encore une simplification, mais pas aussi importante que dans le cas de la rotation sur elle-même. Copernic avait encore besoin des épicycles, quoiqu'en nombre plus réduit que dans le système de Ptolémée. Ce n'est pas avant les lois découvertes par Kepler que la nouvelle théorie copernicienne n'acquit toute sa simplicité.

A part l'effet révolutionnaire sur l'imagination cosmique, les grands mérites de la nouvelle astronomie étaient au nombre de deux : premièrement, la reconnaissance que ce qui avait été cru depuis l'Antiquité pouvait être faux ; deuxièmement, que la marque de la vérité scientifique est la collection patiente de faits, combinée avec des hypothèses audacieuses sur les lois sous-jacentes expliquant d'un seul coup tous les faits d'observation. Aucun de ces deux mérites n'est aussi complètement développé chez Copernic qu'il ne l'est chez ses successeurs, mais tous les deux sont déjà présent à un certain degré dans ses travaux.

[Enfin l'idée que les vérités scientifiques sont toujours provisoires n'est pas encore clairement établie au XVIIe siècle, et encore moins au XVIe. Elle n'apparaîtra en fait clairement qu'au début du XXe siècle, quand "les deux petits nuages" dont parlait en 1900 Lord Kelvin dans la théorie achevée de la physique (l'impossibilité de mesurer la vitesse par rapport à l'éther et les incohérences dans la modélisation du rayonnement du corps noir) donneront naissance respectivement à la relativité restreinte puis générale, et à la mécanique quantique.]

Rejet par les autorités religieuses du temps de Copernic y compris Luther avec des arguments obscurantistes classiques

Certains des hommes auxquels Copernic fit part de sa théorie étaient des luthériens allemands, mais quand Luther en eut vent, il fut profondément choqué. "Les gens prêtent attention, dit-il, à un astronome amateur sorti de nulle part qui s'efforce de montrer que c'est la Terre qui tourne, et non les cieux ou le firmament, le Soleil et la Lune. [Comme Luther avait avec justesse pourfendu les dogmes de l'Eglise catholique, il se croyait à présent une autorité sur tout, comme Sophie Marceau qui, parce qu'elle avait un joli minois, était interrogée sur ce qu'elle pensait de la guerre en Yougoslavie, et avait répondu : "C'est bête."]

Quiconque, poursuit Luther, veut apparaître intelligent se doit d'élaborer un nouveau système, qui de tous les systèmes est bien sûr le meilleur. Ce fou [Copernic] souhaite renverser toute la science astronomique ; mais les Ecritures sacrées nous disent que Joshua donna l'ordre au Soleil de rester immobile [pendant un temps ; ce qui prouve que sinon c'était lui qui se déplaçait...] et non à la Terre." [Luther avait traduit la Bible en allemand, donc il savait de quoi il parlait...]

Calvin, de la même façon, démolit Copernic avec le texte suivant : "Le monde [i.e. la Terre] aussi est stabilisé, de telle sorte qu'il ne peut pas bouger." (Ps. XCIII, 1). Et il s'exclama : "Qui s'aventurera à placer l'autorité de Copernic au-dessus de celle du Saint-Esprit ?"

Le clergé protestant était au moins aussi bigot que les ecclésiastiques catholiques ; cependant rapidement il y eut plus de liberté de spéculation dans les pays protestants que dans les pays catholiques. La raison est que dans les pays protestants le clergé avait moins de pouvoir.

La caractéristique principale du protestantisme est le schisme, pas l'hérésie. Le schisme conduisit à des Eglises nationales ; et les Eglises nationales n'eurent pas suffisamment de pouvoir pour contrôler le gouvernement laïc. Ce fut clairement un gain pour la connaissance, car les Eglises quelles qu'elles soient s'opposèrent, toujours et partout, tant qu'elles purent à toute innovation qui permettait d'accroître le bonheur et le savoir sur Terre [et qui par conséquent amoindrissait le pouvoir des Eglises, qui a toujours été en réalité un pouvoir sociologique et politique au bénéfice d'une élite, voir mon cours de finance de 2008].

Tycho Brahé

Copernic n'était pas en mesure de fournir des évidences décisives et concluantes en faveur de son hypothèse, et pendant longtemps les astronomes la rejetèrent. L'astronome de premier plan suivant est Tycho Brahé (1546-1601). Il adopta une position intermédiaire : il soutint que le Soleil et la lune tournaient autour de la Terre, mais que les planètes [autre que la Terre donc, qui a l'époque n'était pas comptée comme une planète] tournaient autour du Soleil.

Sur le plan théorique, Brahé ne fit pas preuve d'originalité. Il apporta cependant deux bonnes raisons de contredire la théorie d'Aristote selon laquelle tout ce qui était au-delà de la lune était fixe. Une fut l'apparition d'une nouvelle étoile en 1572, dont on put vérifier qu'elle ne présentait aucun changement de parallaxe au cours du temps, et devait donc être très éloignée au-delà de la lune. L'autre raison était dérivée de l'observation des comètes, dont on comprit aussi qu'elles venaient de très loin. Le lecteur se rappellera que dans la doctrine d'Aristote les évolutions, apparitions et disparitions n'ont lieu que dans la sphère sublunaire ; cette déclaration, comme toutes les autres affirmations qu'Aristote proféra en matière de vérité scientifique, s'avéra un obstacle au progrès.

L'importance de Tycho Brahé n'était pas en tant que théoricien, mais en tant qu'observateur, tout d'abord sous le patronage du roi du Danemark, puis sous celui de l'empereur Rudolf II. Il établit un catalogue d'étoile, et nota la position précise des planètes au cours du temps, pendant de nombreuses années. Vers la fin de sa vie, Kepler, alors un jeune homme, devint son assistant. Les observations de Brahé s'avérèrent pour Kepler une mine d'or.

Johannes Kepler

Johannes Kepler (1571-1630) est un exemple extraordinaire de ce que peut produire avec de la patience quelqu'un qui n'est pas un grand génie. C'est le premier astronome d'importance après Copernic à avoir souscrit à l'hypothèse héliocentrique ; mais les données de Tycho Brahé montraient qu'elle ne pouvait pas être tout à fait comme l'avait décrite Copernic. Kepler était influencé par le pythagorisme [c'est-à-dire une sorte de rapport mystique aux nombres et aux formes géométriques], et était plus ou moins enclin à une forme de religion du dieu solaire, bien qu'il fût par ailleurs un bon protestant. Ces motifs, sans doute, lui fournirent un biais en faveur de l'héliocentrisme. Son pythagorisme le poussa aussi à suivre le Timée de Platon c'est-à-dire à supposer qu'une signification cosmique devait être attachée aux cinq polyèdres réguliers. Il les utilisa pour élaborer des hypothèses dans son esprit ; enfin, par un coup de chance, l'une de ses hypothèses s'avéra être la bonne.

La grande réussite de Kepler est la découverte de ses trois lois du mouvement planétaire. Les deux premières, il les publia en 1609, et la troisième en 1619. La première loi de Kepler énonce que les planètes décrivent des orbites elliptiques, dont le Soleil occupe un des deux foyers. La deuxième loi dit, pour chaque planète, qu'une ligne fictive qui joindrait le Soleil à la planète balaie des aires égales en des temps égaux. Sa troisième loi dit que le carré de la période de révolution d'une planète est dans une proportion fixe [i.e. la même pour toutes les planètes] avec le cube de sa distance moyenne au Soleil.

Il faut dire un mot d'explication de l'importance de ces lois.

Les deux premières lois, à l'époque de Kepler, ne pouvaient être prouvées que dans le cas de Mars ; en ce qui concernait les autres planètes, les observations étaient seulement compatibles, mais pas susceptibles d'offrir une confirmation définitive. Les confirmations décisives pour les autres planètes arrivèrent cependant relativement rapidement.

[La distinction entre "compatible" et "démonstration décisive" mériterait des développements de la part de Russell. En effet, la science ne formule que des hypothèses "compatibles" ; on appelle ça des "explications". Elles deviennent "décisives" quand ces explications permettent de prévoir d'autres phénomènes qu'ensuite on peut effectivement observer. Des quels s'agit-il en ce qui concerne les deux premières lois de Kepler ?]

Avant les ellipses de Kepler, les épicycles

La découverte de la première loi, selon laquelle les planètes décrivent des ellipses, demandait un plus grand effort d'émancipation par rapport à la tradition que ne l'imagine un esprit moderne. Une chose sur laquelle tous les astronomes, sans exception, s'accordaient était que les mouvements célestes étaient circulaires, ou résultats de la composition de mouvement circulaires [comme le serait par exemple celui de la lune si la Terre décrivait un cercle parfait autour du Soleil, et la lune un cercle parfait autour de la Terre].

Quand les cercles eux-mêmes étaient jugés insatisfaisants pour expliquer le mouvement d'une planète, on utiliisait des épiclyces. Un épicycle est la courbe tracée par un point d'un cercle [ou un point du disque], quand ce cercle roule sur un autre cercle. Par exemple : prenez une grande roue, posez-la et attachez-la par Terre à plat ; prenez une roue plus petite qui a un crayon qui la traverse [quelque part mais pas au centre], et faites rouler la petite roue (elle aussi par Terre et à plat) autour de la grande roue, avec la pointe de crayon qui touche par Terre [et imaginer le sol comme une grande feuille de papier]. Alors la trace du crayon sur le sol sera un épicycle. La trace de la lune, en relation avec le Soleil, est aussi en gros de cette nature [sauf que là c'est le centre de l'orbite de la lune qui glisse le long de l'orbite de la Terre -- R. n'est pas prof de maths...] : approximativement, la Terre décrit un cercle autour du Soleil et la lune décrit un cercle autour de la Terre.

Mais ce ne sont que des approximations. A mesure que les observations devenaient plus précises, on découvrit qu'aucun système d'épicycles ne pouvait exactement s'ajuster aux faits.

L'hypothèse de Kepler, découvrit-il, était bcp plus proche d'un accord avec les positions observées de Mars que ne l'était l'hypothèse de Ptolémée, ou même de Copernic.

Abandon des hypothèses "scientifiques" fondées sur l'esthétique, même si les scientifiques modernes y sont encore sensibles (cf. livre de Graham Farmelo "It must be beautiful")

La substitution des ellipses à la place des cercles impliquait l'abandon du biais esthétique qui avait gouverné l'astronomie depuis Pythagore. Le cercle était une figure parfaite, et les corps célestes tournant dans les cieux étaient des corps parfaits -- à l'origine des dieux, et même chez Platon et Aristote en lien étroit avec des dieux. Il semblait évident qu'un corps parfait devait décrire une orbite parfaite. En outre, puisque les corps célestes de meuvent librement, sans être poussés ou tirés, leur mouvement doit être "naturel".

Il était facile de considérer que le cercle était quelque chose de naturel, tandis que l'ellipse ne l'était pas [même si les coniques, pour un esprit moderne, sont très jolies aussi...]. Ainsi de nombreux préjugés profondément ancrés devaient être éliminés avant que la première loi de Kepler pût être acceptée. Aucun ancien, pas même Aristarque de Samos n'avait anticipé une telle hypothèse.

La deuxième loi de Kepler

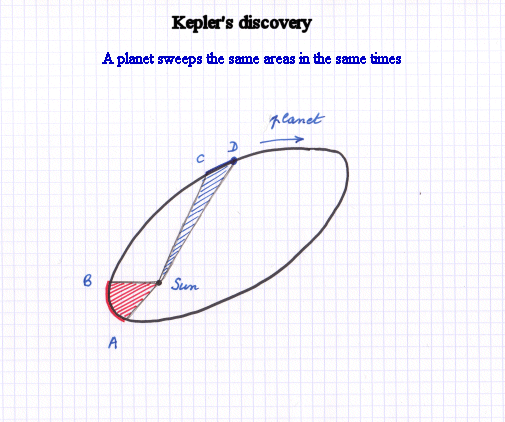
Deuxième loi de Kepler. (Avec la première loi, elle joua un grand rôle dans le développement du calcul intégral.)

La deuxième loi porte sur la vitesse de la planète le long de son ellipse. Selon cette loi, la vitesse de la planète n'est pas uniforme le long de son orbite. Mais l'aire balayée dans le temps entre deux dates t₁ et t₂ est dans une proportion fixe de t₂- t₁. Ainsi en un mois, qu'elle soit près ou loin du Soleil, la planète balaiera la même aire. Pour cette raison quand la planète est plus proche du Soleil, elle va plus vite que quand elle en est éloignée. A nouveau, ce résultat était choquant : une planète se devait d'avoir un mouvement "parfait" à vitesse uniforme, et non pas se presser parfois et musarder à d'autres moments.

La troisième loi de Kepler

La troisième loi [que Kepler mit très longtemps à trouver, et ne publia que dix ans après les deux premières] était importante car elle comparait les mouvements de différentes planètes, tandis que les deux premières ne traitaient que de planètes considérées chacune isolément. La troisième loi dit : si r est la distance moyenne de la planète au Soleil, et T est le temps d'une révolution complète de la planète sur son orbite elliptique, alors le cube de r est dans une proportion fixe du carré de T, quelle que soit la planète considérée. Cette loi apportait la preuve (pour ce qui concerne le système solaire) de la loi de la gravitation de Newton en inverse du carré.

[Là encore, Russell n'est ni mathématicien, ni physicien, ni astronome. Ce n'est pas particulièrement la 3e loi qui confirme la loi de la gravitation de Newton. Ce qui est vrai c'est que la loi d'inertie et la loi de la gravitation, toutes deux dues à Newton, expliquent les trois lois de Kepler, et c'était un triomphe éblouissant pour la théorie de Newton, qui est mathématiquement relativement simple, mais au-delà de tout ce que pouvaient comprendre les Anciens, et même bcp de ses contemporains. Wallis disait de Newton qu'il avait perdu l'esprit ("was out of his mind").

Ce triomphe éblouissant avait nécessité l'invention du calcul intégral et différentiel.

De nos jours on exprime plutôt la 3e loi comme ceci :

le carré de la période orbitale d'une planète est dans une proportion fixe avec le cube du demi grand axe de son orbite,

voir chapitre sur la gravitation du premier livre de L. Susskind dans la série "Le minimum théorique"..]

Nous en dirons plus un peu plus loin.

Galilée

Galilée (1564-1642) est le plus grand des fondateurs de la science moderne, jusqu'à Newton (1642-1727) que l'on peut considérer comme encore plus grand. Il était né le jour où Michelange mourut, et il mourut l'année où Newton naquit. Je signale ce fait à ceux (s'il y en a) qui croient encore en la métempsychose. Galilée est important en tant qu'astronome, mais peut-être encore davantage en tant que fondateur de la dynamique.

[La dynamique est la branche de la physique qui étudie l'évolution dans le temps d'un système. L'autre branche est la statique.]

Galilée découvrit tout d'abord l'importance de l'accélération en dynamique. "Accélération" veut dire changement dans la vélocité, considérée comme un vecteur, donc que le changement soit en magnitude ou en direction. Ainsi un corps se mouvant uniformément sur une trajectoire circulaire a une vélocité qui change constamment, non pas en magnitude, mais en direction. Son accélération est un autre vecteur qui pointe constamment vers le centre.

Avant Galilée les mouvements considérés comme "naturels" étaient sur Terre la seule ligne droite, et dans le ciel la ligne droite et le cercle.

On pensait aussi, depuis Aristote, que sur Terre le mouvement naturel en ligne droite s'arrêtait "naturellement" au bout d'un moment -- s'il n'était pas, sous une forme ou sous une autre, poussé à continuer.

En opposition à cette vue [datant d'Aristote, Ô grand Aristote...], Galilée soutenait qu'un corps laissé à lui-même, si aucune force ne s'appliquait sur lui, continuerait à se mouvoir à vitesse uniforme sur une trajectoire en ligne droite.

Un quelconque changement, soit en vitesse soit en direction, exigeait qu'une "force" s'applique sur lui. Ce principe fut énoncé par Newton sous la forme de la première loi de Newton du mouvement. Elle est aussi appelée loi d'inertie.

[L' "inertie" est un concept un peu obscur de la physique newtonienne, concept utilisé dans la présentation d'origine de la théorie de Newton, et encore de nos jours au lycée. La même chose, dans une moindre mesure, est vraie du concept de "force".

Elle n'apparait que dans l'équation sur des infinitésimaux : Fdt = mdv (équivalente à F = m gamma) qui joue un rôle important dans l'explication de la pression par un gaz sur les parois d'un récipient, par la moyennisation d'une multitude de chocs de molécules exerçant chacune de manière "ponctuelle" dans l'espace et dans le temps une force infinie..

Penser aussi à la façon dont une boule de billard change de direction en tapant contre une bande : que ce passe-t-il au juste lors du choc ; quelle force est exercée ? pendant combien de temps ?

De nos jours, dans une approche plus conceptuelle de la physique, on préfère se focaliser sur l' "énergie" d'un système (et aussi sur sa "quantité de mouvement", voir le théorème de Noether). Pour un système isolé, son énergie est constante. Et les calculs dynamiques sont effectués à partir des équations d'Euler-Lagrange.

Voir "Le minimum théorique" de Leonard Susskind. qui donne une bien meilleure présentation de la dynamique pour les néophytes que ne le fait Russell. Le livre de Susskind peut être lu par quiconque a un bac scientifique, et est prêt à monter un peu plus haut avec Susskind pour guide de montagne.]

Je retournerai au principe d'inertie plus loin, mais il faut d'abord rentrer un peu dans le détail des découvertes de Galilée.

Loi de la chute des corps

Galilée fut le premier à établir la loi de la chute des corps [précisons ce que veut dire Russell : la "loi de la chute des corps" dit qu'un objet lâché verticalement, sans vitesse initiale, d'une position donnée, aura parcouru, au temps t, une distance x vers le bas proportionnelle à t au carré ; un peu de maths montre alors que sa vitesse est proportionnelle à t ; et son accélération est constante ; sur Terre elle a la valeur g = 9,81 mètres par seconde carrée, c'est-à-dire que chaque seconde la vitesse augmente de 9,81 mètres par seconde].

Cette loi, si l'on introduit le concept d' "accélération", est d'une grande simplicité. Elle dit que, quand un corps tombe en chute libre, son accélération est constante, sauf à prendre en compte l'effet minime [si le corps a une masse volumique élevée -- une boule de pétanque, pas une plume d'oiseau] de la résistance de l'air ; en outre, cette accélération est la même pour tous les corps, lourds ou légers, grands ou petits. [Cependant près de quatre siècles après Galilée, allez dans un bar et demandez si ce sucre et ce verre vont tomber en même temps par Terre ; tout le monde vous dira "non, le verre qui est plus lourd tombera plus vite" (merci Aristote encore et toujours...).]

La démonstration expérimentale définitive de cette loi ne fut pas possible tant qu'on n'eut pas inventé la pompe à vide, ce qui arriva en 1654. Après cette date, il fut possible d'observer des corps en chute libre dans un vide presque parfait, et on vérifia que des billes de plomb tombaient ni plus ni moins vite que des plumes d'oiseau. On vérifia aussi qu'il n'y avait pas de différence mesurable entre la chute de deux corps, un lourd et un léger, fait de la même substance.

Jusqu'à l'époque de Galilée on pensait qu'une grosse masse de plomb devait tomber plus vite qu'une petite masse de plomb, mais Galilée montra que ce n'était pas le cas. [Du reste -- j'en ai déjà parlé mais je répète -- si on avait imaginé l'expérience dans laquelle la grosse masse de plomb est scindée en deux en cours de chute, on aurait conclu que ça ne changeait rien et que donc la masse ne jouait pas de rôle.]

Les mesures de longueur et surtout de temps, à l'époque de Galilée, n'étaient pas aussi précises qu'elles le sont devenues aujourd'hui ; cependant il arriva à la bonne loi pour la chute des corps. [Il utilisa une intuition remarquable : il se dit qu'observer une bille glissant sur une planche inclinée bien savonnée était équivalent à la voir en chute libre, mais avec une force de gravitation moindre ; il fit ses expériences sur les plans inclinés, et extrapola.]

Si un corps est en chute libre dans le vide, sa vélocité augmente à un taux constant. A la fin de la première seconde sa vélocité sera de 32 pieds par seconde ; à la fin de la deuxième, 64 pieds par seconde ; à la fin de la troisième 96 pieds par seconde ; et ainsi de suite. L'accélération, c'est-à-dire le taux d'accroissement de la vélocité, est toujours la même ; chaque seconde, l'accroissement de la vélocité est (approximativement) 32 pieds par seconde.

Balistique

Galilée étudia aussi la trajectoire des projectiles [ce qu'on appelle la balistique], un sujet important pour son employeur, le duc de Toscane. On pensait qu'un projectile tiré horizontalement se déplaçait horizontalement pendant un moment, puis soudainement commençait une chute verticale. Galilée montra que, si l'on fait une fois de plus abstraction de la résistance de l'air, la vélocité horizontale reste constante, en accord avec la loi d'inertie, mais une vélocité verticale doit être ajoutée, qui suit la loi de la chute des corps. Pour trouver la vitesse instantanée d'un corps à un moment t quelconque, combinez deux vecteurs : la vitesse horizontale (constante) et la vitesse verticale (qui suit la loi v₀ + 1/2 gt²). Un calcul simple montre que la trajectoire suivie par le projectile est une parabole, et l'observation attentive d'une expérience le confirme, encore une fois à la résistance de l'air près.

La présentation ci-dessus est un exemple d'un principe qui se révéla immensément fructueux en dynamique, le principe selon lequel, quand plusieurs forces agissent en même temps, l'effet combiné correspond à l'addition des vecteurs forces. C'est un cas particulier de la loi du parallélogramme [je m'éloigne des "explications" de Russell, qui sont du Euclide mal digéré].

Le paragraphe suivant ne mérite pas d'être traduit : Suppose, for example, that you are on the deck of a moving ship, and you walk across the deck. While you are walking the ship has moved on, so that, in relation to the water, you have moved both forward and across the direction of the ship's motion. If you want to know where you will have got to in relation to the water, you may suppose that first you stood still while the ship moved, and then, for an equal time, the ship stood still while you walked across it. The same principle applies to forces. This makes it possible to work out the total effect of a number of forces, and makes it feasible to analyse physical phenomena, discovering the separate laws of the several forces to which moving bodies are subject. It was Galileo who introduced this immensely fruitful method.

Exposé du XVIIe siècle, et loi d'inertie

Dans ce que j'ai dit, je me suis efforcé de parler, autant que possible, en utilisant le langage du XVIIe siècle. Le langage moderne est différent à plusieurs importants égards, mais pour expliquer ce que le XVIIe siècle a accompli il est souhaitable d'adopter ses modes d'expression pour le moment.

[Euh, ça se discute. Mais c'est sans doute vrai pour la philosophie de Platon ou d'Aristote, car sinon elle n'a plus aucun sens, et ne se révèle qu'être un charabia plus ou moins attachant de gens cherchant à comprendre le monde (et surtout à imposer leurs vues sociales et politiques, comme le fait encore aujourd'hui la religion). Alors Russell pense que c'est aussi nécessaire pour la science, ce qui est faux.]

La "loi d'inertie" [un corps en déplacement libre, i.e. sans force appliquée sur lui, continue indéfiniment sur une trajectoire rectiligne à vitesse uniforme] expliqua un puzzle que, avant Galilée, le système copernicien n'était pas capable d'expliquer. Comme on l'a dit plus haut, si vous lâchez une pierre depuis le sommet d'une tour, elle va tomber exactement au pied de la tour, pas un peu plus à l'ouest ; cependant la Terre tourne, et elle devrait avoir un peu glissé vers l'est pendant la chute de la pierre. La raison pour laquelle on n'observe pas de déplacement horizontal de la pierre est que la pierre a elle aussi la même vitesse que la Terre vers l'est. [Tout cela s'appelle aussi "la relativité galiléenne", à ne pas confondre avec "la relativité einsteinienne", qui a généralisé la relativité galiléenne.]

En fait, si la tour était suffisamment haute, il y aurait au contraire l'effet opposé à celui prédit par les opposants à Copernic. Le sommet de la tour étant plus éloigné du centre de la Terre, la pierre aurait une composante horizontale de vitesse plus élevée que la surface de la Terre, et donc elle tomberait un peu vers l'est. Cet effet était, cependant, trop faible pour être observé [et en particulier beaucoup plus faible que l'effet de la résistance de l'air].

Système héliocentrique, et découvertes par Galilée

Galilée adopta ardemment le système héliocentrique ; il correspondait par courrier avec Kepler, et acceptait ses découvertes. Ayant entendu dire qu'un Hollandais avait récemment inventé un télescope, Galilée en fabriqua un lui-même, et très rapidement fit un grand nombre de découvertes astronomiques stupéfiantes.

Il découvrit que la Voie Lactée consistait en une myriade d'étoiles distinctes. Il observa les phases de Vénus, dont Copernic savait que sa théorie prédisait l'existence, mais qu'on ne peut pas observer à l'oeil nu. Il découvrit les satellites de Jupiter, qu'en l'honneur de son employeur, il nomma "sidera medicea".

On découvrit que ces satellites obéissaient aux lois de Kepler.

Il y avait cependant une difficulté. Il y avait toujours eu sept corps célestes, les cinq planètes et le Soleil et la lune ; et le chiffre sept était un nombre sacré. Le sabbat n'est-il pas le septième jour ? N'y a-t-il pas sept branches aux chandeliers, et les sept églises d'Asie ? Que pouvait-il y avoir de plus approprié que les sept corps célestes ?

Mais il fallait maintenant ajouter les quatre lunes de Jupiter, et cela faisait onze -- un nombre sans propriétés mystiques.

Sur cette base, les traditionnalistes dénoncèrent le télescope, refusèrent de regarder dans son oculaire, et maintinrent que ce qu'il montrait n'était que des illusions d'optique.

Galilée écrivit à Kepler disant qu'ils pourraient avoir une franche rigolade ensemble en discutant de la stupidité de la "foule" ; le reste de la lettre montre clairement que "la foule" consiste en les professeurs de philosophie, qui essaient de nier l'existence des lunes de Jupiter, "en utilisant des arguments qui transpercent la logique comme s'ils étaient des incantations magiques".

[Malheureusement cet esprit magique existe encore même chez des gens soi-disant "éduqués". Ils peuvent vous parler des "nombres sacrés", de 'la communication profonde assistée" avec des moribonds muets par des magnétiseuses (des paumées en déshérence, qui cherchent à berner les crédules -- et elles-mêmes -- avec cette activité), de l'astrologie, avec les signes du zodiaque, même si les étoiles ont beaucoup bougé depuis l'invention des signes dans les constellations, etc. Sans faire d'esprit de type II de Bachelard, il y a des jours où c'est désespérant.]

Condamnation par l'Inquisition

Galilée, comme chacun sait, fut condamné par l'Inquisition, d'abord en privé en 1616, puis en public en 1633. A cette deuxième occasion, il se rétracta, et promit de ne plus jamais maintenir que la Terre tournait autour du Soleil ou sur elle-même. L'Inquisition parvint avec succès à mettre fin à la science en Italie pour plusieurs siècles.

Mais elle ne parvint pas à empêcher les hommes de science d'adopter la théorie héliocentrique. Et son obstination stupide fit beaucoup de tort à l'Eglise.

Par chance il y avait les pays protestants, où le clergé, quoique tout aussi soucieux de mettre un terme à la science, n'avait pas le pouvoir de contrôler l'Etat ni l'activité des hommes de science.

Newton

Newton (1642-1727) accomplit le triomphe final et complet pour lequel Copernic, Kepler et Galilée avaient pavé la voie. Newton, partant de ses propres trois lois du mouvement -- dont les deux premières sont dues à Galilée --, prouva que les trois lois de Kepler sont équivalentes à la proposition que chaque planète, à chaque instant, subit une accélération vers le Soleil inversement proportionnelle au carré de la distance au Soleil.

Il montra que les accélérations vers la Terre et le Soleil, suivaient la même formule, et expliquaient le mouvement de la lune, et que l'accélération d'un corps en chute libre à la surface de la Terre est la même que celle de la lune, suivant la loi en inverse du carré de la distance.

[Une fois de plus, quand il expose de la vraie science, même élementaire, Russell devient tout de suite confus. Ce n'est pas tant la loi en inverse du carré de la distance (loi n°3 ci-dessous) qui est étonnante en ce qui concerne la lune, c'est que dans son orbite quasi circulaire autour de la Terre elle suit en fait F = m gamma !

Pour être plus clair, Newton énonça les trois lois suivantes :

1) un corps sur lequel aucune force ne s'applique est soit au repos, soit en mouvement rectiligne uniforme

2) pour un corps de masse m : F = m gamma

3) pour deux corps de masse m et M et séparés par une distance d : F = m M G / d² ]

Newton définit la "force" comme la cause du changement dans le mouvement, c'est-à-dire de l'accélération. Il fut alors capable d'énoncer sa loi de la gravitation universelle : "Tout corps attire tout autre corps avec une force proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare."

A partir de ses trois lois, il fut capable de déduire tous les mouvements [au-delà de ce qu'avait déjà expliqué Galilée avec les lois 1 et 2 ci-dessus] : les mouvements des planètes et de leurs satellites, l'orbite des comètes, et même les marées.

On découvrit plus tard que même les petites anomalies dans les orbites théoriquement elliptiques des planètes s'expliquaient avec les lois de Newton. [C'est ainsi que Le Verrier, par des calculs, en 1846 prédit l'existence d'une planète inconnue. On vérifia rapidement sa prédiction et on l'appela Neptune.]

Le triomphe était si complet que Newton présenta le danger de devenir un nouvel Aristote, et d'imposer une barrière insurmontable au progrès ultérieur. [On notera par ailleurs qu'il resta toute sa vie très bigot anglican, anti-papiste, et aussi alchimiste ; il fut à partir d'un peu plus de 50 ans le responsable de la monnaie en AngleTerre. Voir deuxième moitié de ce chapitre, décrivant Newton.]

En AngleTerre, il fallut attendre un siècle après la mort de Newton pour que les savants se libèrent suffisamment de son autorité pour faire à nouveau des travaux originaux et importants sur des sujets que Newton avaient déjà abordés.

Autres avancées de la science au XVIIe siècle

Le 17e siècle fut remarquable, non seulement en astronomie et dynamique, mais dans beaucoup d'autres domaines en lien avec la science.

Considérons d'abord la question des instruments scientifiques. (Sur le sujet, voir le chapitre "Scientific Instruments" dans A History of Science, Technology, and Philosophy in the Sixteenth and Seventeenth Centuries, par A. Wolf.) Le microscope fut inventé juste avant le 17e siècle, vers 1590. Le télescope fut inventé en 1608, par un Hollandais du nom de Lippershey, bien que ce soit Galilée qui le premier en fit un usage sérieux dans un but scientifique. Galilée inventa aussi le thermomètre -- en tout cas cela semble probable. Son élève Torricelli inventa le baromètre. Guericke (1602-1686) inventa la pompe à vide. Les horloges, même si elles existaient déjà, furent considérablement améliorées au 17e siècle, pour une bonne part à la suite des travaux de Galilée. Grâce à toutes ces inventions, les observations scientifiques devinrent infiniment plus précises et plus étendues que ce qu'elles avaient été auparavant.

[On notera que Galilée avait besoin de mesurer le temps de manière précise pour établir sa loi x = 1/2 g t². Certains pensent qu'il utilisait des comptines qu'il chantait en regardant la chute de ses billes glissant sur des plans inclinés (il ne fallait pas qu'elles roulent, pour éviter l'énergie cinétique de rotation).]

Ensuite, il y eut d'importants travaux dans d'autres sciences que l'astronomie et la dynamique. Gilbert (1540-1603) publia son grand livre sur les aimants et le magnétisme en 1600. Harvey (1578-1657) découvrit la circulation sanguine, et publia sa découverte en 1628. Leeuwenhoek (1632-1723) découvrit les spermatozoïdes, bien qu'il semble qu'un autre homme, Stephen Hamm, les eût découvert quelques mois plus tôt ; Leeuwenhoek découvrit aussi les protozoaires et autres organismes unicellulaires, et même les bactéries [qui sont aussi unicellulaires].

Robert Boyle (1627-1691) était, comme les enfants l'apprenaient quand j'étais jeune [Russell est né en 1872], "le père de la chimie et le fils du Earl of Cork" ; on s'en souvient aujourd'hui surtout pour la "loi de Boyle" [appelée en France loi de Mariotte], qui dit qu'une quantité donnée de gaz dans un récipient fermé à une température donnée a une pression inversement proportionnelle au volume. [Là encore une toute petite équation en dirait bcp plus que cette expression verbale, mais bon on n'est pas dans un ouvrage de physique même élémentaire.]

En mathématiques

Je n'ai rien dit jusqu'à présent des avancées en mathématiques pures ; mais elles furent elles aussi très grandes, et indispensables à beaucoup des travaux réalisés en sciences physiques. Napier [appelé aussi Neper] publia son invention des logarithmes en 1614. La géométrie analytique [i.e. utilisant un système de coordonnées pour repérer les points et faire correspondre des équations aux figures] fut le résultat du travail de plusieurs mathématiciens du 17e siècle, parmi lesquels les plus grandes contributions furent faites par Descartes. La calcul différentiel et intégral fut inventé indépendamment par Newton et Leibniz [Newton fit sans doute les plus grandes contributions et certainement le plus grand usage de ce calcul, mais on utilise encore de nos jours les notations de Leibniz -- qui ont des avantages et des inconvénients]. Le calcul différentiel et intégral joue un rôle fondamental dans toutes les mathématiques supérieures. J'ai mentionné ici seulement les accomplissements les plus extraordinaires en mathématiques pures ; il y en eut de nombreux autres de grande importance aussi.

La conséquence des travaux scientifiques que nous venons de considérer fut que le point de vue sur l'univers des hommes instruits en fut complètement transformé. Au début du siècle [dix-septième], Sir Thomas Browne fut impliqué dans des procès pour sorcellerie ; à la fin du siècle, une telle chose eût été impossible.

A l'époque de Shakespeare, les comètes étaient encore considérées comme des signes [envoyés à l'humanité, par... des déités ?] ; après la publication des Principia de Newton en 1687, on savait que lui et Halley avaient calculé les orbites de certaines comètes, et qu'elles se conformaient de la même façon que les planètes à la loi de la gravitation.

Le règne de la loi avait établi son emprise sur l'imagination des hommes, rendant des pratiques comme la magie et la sorcellerie incroyables.

En 1700 la mentalité des hommes éduqués était complètement moderne [on ne peut plus en dire autant au début du XXIe siècle :-((( ]. En 1600, sauf pour quelques exceptions, elle était encore médiévale.

Dans le reste de ce chapitre, je vais m'efforcer d'exposer brièvement les croyances philosophiques qui apparurent à la suite de la science du 17e siècle, et en quoi la science moderne diffère de celle de Newton.

Croyances philosophiques conséquences des réussites scientifiques

La première chose à noter est la disparition de toute trace d'animisme dans les lois de la physique. Les Grecs, bien qu'ils ne le dirent pas explicitement, considéraient évidemment le pouvoir de créer le mouvement comme une marque de la vie. Le bon sens indiquait que les animaux se mouvaient eux-mêmes, tandis que les choses inertes étaient seulement mues par des forces externes. L'âme d'un animal, chez Aristote, avait diverses fonctions, l'une d'entre elles étant de faire se mouvoir le corps de l'animal.

Le Soleil et les planètes, dans la pensée grecque, pouvaient tout à fait être des dieux, ou du moins être régulés par des dieux. Anaxagore pensait autrement, mais il était considéré comme impie. Démocrite pensait aussi autrement, mais les philosophes suivants, à l'exception d'Epicure, n'y prêtèrent pas attention, et préférèrent Platon et Aristote. Les 47 ou 55 "unmoved movers" [moteurs qui eux-mêmes ne bougent pas] d'Aristote sont des esprits divins, et sont la source ultime de tout mouvement dans l'univers. Laissé à lui-même, un corps inanimé quelconque s'arrête rapidement de bouger ; ainsi l'opération de l'âme sur la matière doit être continue si le mouvement ne doit pas s'arrêter.

Tout ceci fut bouleversé par la première loi du mouvement [un corps laissé à lui-même soit reste immobile, soit reste indéfiniment en mouvement rectiligne uniforme]. La matière inerte, une fois mise en mouvement, continuera à se mouvoir indéfiniment, tant qu'une cause externe ne l'arrêtera pas. En outre, les causes externes de changement se révélèrent être matérielles [par opposition à divines] chaque fois qu'on pouvait les étudier. Le système solaire, en tout cas, continuait à tourner sur sa lancée par sans apport extérieur et selon des lois ; aucune interférence venant d'ailleurs n'était nécessaire.

Il pouvait encore sembler y avoir besoin de Dieu pour mettre le mécanisme en mouvement.

[C'est par exemple le mystère actuel du Big Bang.

Mais tout porte à penser que les esprits de XXIIe siècle auront des explications non-divines du Big Bang, donnant plutôt une description entièrement nouvelle du rapport entre les hommes, leur esprit, leurs perceptions, et les choses perçues.]

Les planètes, dans le système newtonien, étaient lancées au départ par la main de Dieu. Mais une fois qu'Il avait donné cette impulsion initiale, et décrété les lois de la gravitation, tout continuait par soi-même sans nécessiter d'autre intervention divine.

Quand Laplace suggéra que les mêmes forces qu'on voit à l'oeuvre maintenant pouvaient aussi avoir causé l'apparition des planètes à partir du Soleil, la part de Dieu dans la marche de la nature fut encore réduite. Il pouvait rester en tant que Créateur, mais même cela était douteux, puisqu'il n'était pas clair que le monde eût un début dans le temps [on est avant la théorie du Big Bang du physicien/jésuite belge Georges Lemaître].

Des scientifiques pour la plupart encore croyants, mais séparation de leurs croyances et de la science, et abandon de la téléonomie

Bien que la plupart des hommes de science fussent des modèles de piété [à commencer par Newton, qui était même un allumé], la mentalité suggérée par leurs travaux était troublante pour l'orthodoxie, et les théologiens avaient des raisons d'être mal à l'aise.

Une autre conséquence des avancées scientifiques du 17e siècle fut un bouleversement dans la conception de la place de l'homme dans l'univers. Dans le monde médiéval, la Terre était au centre des cieux, et tout avait un but qui concernait l'homme. Dans le monde newtonien, la Terre était une planète mineure dans un système d'une étoile n'ayant rien de notable ; les distances astronomiques étaient tellement grandes que la Terre, en comparaison, était une simple tête d'épingle.

Il semblait peu vraisemblable que cet immense paysage cosmique ait été conçu pour le seul bénéfice de certaines minuscules créatures vivant sur cette tête d'épingle. En outre le concept téléonomique de but, qui depuis Aristote faisait partie intégrante de toute conception "scientifique", était maintenant écarté des procédures scientifiques.

Chacun pouvait continuer à penser que les cieux existaient pour proclamer la gloire de Dieu, mais personne ne pouvait laisser ce genre de croyance interférer dans les calculs astronomiques. Le monde avait peut-être un but, mais les buts téléonomiques n'avaient plus droit de cité dans les explications scientifiques.

Humilité vs orgueil

La théorie copernicienne aurait dû rendre plus humble le genre humain, mais en fait c'est le contraire que se passa, car les triomphes de la science ravivèrent son orgueil.

Le monde antique disparu avait été obsédé par la notion de péché, et cette oppression avait duré jusqu'au Moyen Âge. Etre humble devant Dieu était à la fois correct et prudent, car Dieu punissait l'orgueil. Les épidémies, les inondations, les tremblements de Terre, les Turcs, les Tatares, les comètes laissèrent perplexes les siècles lugubres, et l'on pensait que seule une humilité toujours plus grande pouvait éviter ces calamités. Mais il devint impossible de rester humble face aux triomphes de la science :

"Nature and Nature's laws lay hid in night. God said 'Let Newton be', and all was light."

Dieu, l'enfer, ses autres préoccupations, et les hommes

En ce qui concerne la damnation, sûrement le Créateur de ce vaste univers avait mieux à faire que de s'occuper d'envoyer des hommes en enfer pour de minuscules fautes théologiques. Judas Iscariote pouvait être damné, mais pas Newton, même s'il avait été un arien [du reste c'était un anti-papiste virulent].

Il y avait bien sûr beaucoup d'autres raisons d'être satisfait. Les Tatars avaient été repoussés en Asie, et les Turcs ne représentaient plus une menace. Les comètes avaient été expliquées par Halley, et pour ce qui était des tremblements de Terre, bien qu'ils fussent toujours formidables, ils étaient tellement intéressants que les hommes de science pouvaient difficilement le regretter.

Les pays occidentaux s'enrichissaient rapidement, et étaient en train de devenir les maîtres du monde : ils avaient conquis l'Amérique du Nord et du Sud, ils étaient puissants en Afrique et en Inde, respectés en Chine, craints au Japon.

Quand à tout ceci s'ajoutaient les triomphes de la science, on n'est plus surpris que les hommes du dix-septième siècle se sentissent des êtres supérieurs, pas de misérables pécheurs, bien que ce fût encore ce qu'ils proclamaient le dimanche à la messe ou au culte.

[Mais la messe dominicale n'est qu'une conduite sociale pour marquer son appartenance sociologique à une certaine société et certaines classes sociales, rien de moins et rien de plus. Ce qu'ils y avouent, prétendent ou proclament n'a aucun rapport avec la vie que mènent la plupart des paroissiens le reste de la semaine, où ils se montrent cruels, insensibles, maladivement attachés aux biens matériels, pollueurs irresponsables, indifférents à la misère des autres, etc. Bref des animaux plus primaires encore que les vrais animaux qui sont plus respectueux de l'univers.]

Différence entre la pensée contemporaine et celle à l'époque de Newton

Il y a quelques aspects par lesquels les concepts de la physique théorique moderne diffèrent de ceux du système newtonien.

Abandon du concept de "force" (remarquables explications de Russell, peut-être conseillé par Blackett)

Pour commencer, le concept de "force", qui était prééminent au 17e siècle a été trouvé largement superflu.

La "force", chez Newton, est ce qui cause le changement dans le mouvement, que ce soit en magnitude ou en direction. Cette notion de cause est considérée comme importante. Et la force est pensée comme la sorte de chose dont nous faisons l'expérience quand nous tirons ou poussons quelque chose. Pour cette raison, on pensait que c'était un argument contre la gravitation de souligner qu'elle agit à distance. Et Newton lui-même concédait qu'il devait y avoir un milieu par lequel la force était transmise. [C'était avant le concept de champ introduit par Faraday ; mais cela ne donna pas une nouvelle jeunesse à la force.]

Graduellement, on découvrit que toutes les équations de la dynamique pouvaient être écrites sans utiliser le concept de force. Ce qui était observé était une certaine relation entre l'accélération et la configuration d'un système ; dire que cette relation était produite par l'intermédiaire d'une "force" n'ajoutait rien à notre connaissance.

L'observation montre que les planètes ont à chaque instant une accélération vers le Soleil, qui varie comme l'inverse du carré de la distance au Soleil. Dire que cela est dû à une "force" de gravitation est un artifice verbal, comme de dire que l'opium fait dormir les gens "car il a des vertus dormitives".

Le physicien moderne, par conséquent, se borne à écrire des équations qui déterminent l'accélération [et les autres paramètres de la dynamique] et évite totalement de mot "force".

La "force" était un reste fantomatique de la vision vitaliste des causes du mouvement, et peu à peu le fantôme a été exorcisé.

[Lagrange n'utilisait plus le concept de force, mais ses équations restaient, à la fin, similaires à celles de Newton. Einstein introduisit la courbure de l'espace sous l'effet des masses, et établit son équation liant géométrie de l'espace et tenseur masse-énergie.]

Apports de la relativité et de la mécanique quantique

Jusqu'à l'avènement de la mécanique quantique, rien ne modifia fondamentalement le sens essentiel des deux premières lois du mouvement, c'est-à-dire : les lois de la dynamique sont énoncées en terme d'accélérations.

A cet égard, Copernic et Kepler font partie des Anciens ; ils cherchèrent, eux, des lois décrivant les formes des orbites des corps célestes.

Newton montra clairement que des lois énoncées sous cette forme ne pourraient jamais être autre chose qu'approximatives. Les planètes ne parcourent pas exactement des ellipses, à cause des perturbations introduites par les autres planètes [le problème des trois corps, ou des n corps]. Et les trajectoires ne sont jamais exactement répétées à l'identique d'une orbite à l'autre, pour la même raison. Mais la loi de la gravitation, qui est concernée par les accélérations, était très simple. Et l'on pensa qu'elle était exacte pendant encore deux siècles après Newton. Même après avoir été amendée par Einstein, elle traitait toujours des accélérations.

Il est vrai que la conservation de l'énergie est une loi qui traite des vélocités, pas de l'accélération. Mais dans les calculs qui utilisent cette loi, on est toujours conduit à utiliser les accélérations.

En ce qui concerne les changements apportés par la mécanique quantique, ils sont très profonds, et encore, dans une certaine mesure, controversés [écrit dans les années 40, où la théorie des variables cachées était encore respectée].

Bouleversement de l'espace-temps

Il y a un changement par rapport à la philosophie newtonienne qu'il faut mentionner ici pour finir : celui de l'abandon de l'espace absolu et du temps universel. Le lecteur se souvient d'une mention de cette question dans le chapitre sur Démocrite.

Newton pensait que l'espace était composés de points ["à des positions fixes"], et le temps composé d'instants, tous les mêmes pour tout le monde, qui étaient indépendants des corps et des évènements qui se déroulaient.

En ce qui concernait l'espace, il avait un argument empirique pour soutenir son approche : c'était que des phénomènes physiques nous permettaient de distinguer une rotation dans l'absolu. Par exemple, si une bassine remplie d'eau était mise en rotation [autour de son axe central vertical], l'eau commençait à monter le long des bords internes de la bassine, et on observait un creux au milieu de la surface de l'eau ; mais si la bassine est mise en rotation sans eau dedans alors on n'observe pas ce phénomène.

[Le philosophe des sciences Ernst Mach (1838-1916), qui était une sommité dans la deuxième moitié du XIXe siècle, a bcp cogité sur ce problème. Ses livres ont été des livres de chevet d'Einstein dans sa jeunesse -- jusqu'à ce qu'Einstein se rende compte qu'il pouvait faire dire des choses bcp plus intéressantes à ses propres théories et équations que ne le faisait Mach, et qu'Einstein se désintéresse de la "philosophie scientifique" de Mach. La philosophie scientifique de Mach est une resucée d'Occam mal compris. Mach s'est opposé à Boltzmann et a rejeté l'hypothèse atomique "car on ne pouvait pas voir les atomes" -- ce qui est un argument qui aurait déjà paru rétrograde aux meilleurs présocratiques !!!]

Après l'époque de Newton, l'expérience du pendule de Foucault avait été mise au point, montrant ce qu'on considérait comme une preuve de la rotation de la Terre sur elle-même.

Même dans la vision la plus moderne, la question de la rotation absolue présente des difficultés. Si tous les mouvements sont relatifs [et cela même au simple sens de Galilée], la différence entre l'hypothèse que la Terre tourne, et l'hypothèse que les cieux tournent est purement verbale ; c'est la même chose en quelque sorte que la différence entre "Jean est le père de Jacques" et "Jacques est le fils de Jean".

Mais si les cieux tournent, alors les étoiles lointaines se meuvent plus vite que la vitesse de la lumière, ce qui est considéré comme impossible [là Russell se trompe : c'est seulement près d'un observateur que qqc ne peut pas aller plus vite que la lumière ; dans l'hypothèse acceptée de l'expansion de l'univers, il y a des choses, lointaines, qui s'éloignent de nous plus vite que la vitesse de la lumière].

On ne peut pas dire que les réponses modernes à cette difficulté sont complètement satisfaisantes, mais elles sont suffisamment satisfaisantes pour que la majorité des physiciens acceptent cette vue que le mouvement dans l'espace est purement relatif.

[En fait, même dans cet espace "purement" relatif, on considère qu'il y a des repères galiléens, et d'autres qui ne le sont pas. Les repères galiléens sont ceux où les lois de la dynamique ont une forme simple, du genre F = m gamma ; dans ceux qui sont non galiléens, on a des accélérations ou des forces centrifuges "fictives" comme pour la bassine remplie d'eau.]

Cela, combiné avec la transformation des concepts séparés d'espace et de temps en un espace-temps de Minkowski, a considérablement modifié notre vision de l'univers par rapport à celui qui résultait des travaux de Galilée et Newton.

Mais sur ce sujet, comme sur celui de la mécanique quantique [encore bcp plus effarante pour un esprit traditionnel que la relativité restreinte et générale], je vais m'en tenir là.